关于求解数列的通项公式九种常见类型与方法
何正文
(广东省肇庆市百花中学 526000)
求数列通项题型具有很强的规律性,本文对数列通项公式问题进行九种分类与归纳,希望对广大师生有借鉴之用.
一、形如
这种题型适合用迭加法进行求解.
例1已知数列{an}满足an+1-an=2n+1,a1=1,求数列{an}的通项公式.
解由an+1-an=2n+1得
an=(an-an-1)+(an-1-an-2)+…+(a3-a2)+(a2-a1)+a1
=[2(n-1)+1]+[2(n-2)+1]+…+(2×2+1)+(2×1+1)+1
=(2n-1)+(2n-3)+…+5+3+1
所以数列{an}的通项公式为an=n2.
二、形如
这种题型适合用迭乘法进行求解.

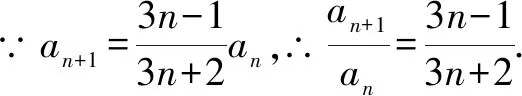
∵a1=3,
三、形如 (其中p,q均为常数)
这种题型可以设an+1+λ=p(an+λ),解出λ,再化为等比数列求解.
例3已知在数列{an}中,a1=1,an+1=2an+3,求an.
解设an+1+λ=2(an+λ),则an+1=2an+λ.
∵an+1=2an+3,∴λ=3,∴an+1+3=2(an+3).
∵a1=1,∴a1+3=4,
∴{an+3}是以4为首项,公比为2的等比数列.
∴an+3=4×2n-1,∴an=2n+1-3.

这种题型可以设an+1+λ·qn+1=p(an+λ·qn),解出λ,再化为等比数列求解.
例4已知数列{an}满足an+1=2an+3×5n,a1=6,求数列{an}的通项公式.
解∵an+1=2an+3×5n,设an+1+λ·5n+1=2(an+λ×5n),则an+1=2an-3λ×5n.
∵an+1=2an+3×5n,∴λ=-1.
∴an+1-5n+1=2(an-5n).∵a1=6,a1-5=1,
∴数列{an-5n}是首项为1,公比为2的等比数列.
∴an-5n=1×2n-1,即an=2n-1+5n.
五、形如
这种题型可以先由n=1求出a1,再由递推式求n≥2时的通项公式,最后一定要检验n=1该通项公式是否满足.如满足,则所求通项公式为整个函数的通项公式,如不满足,则最后结果要以分段函数的形式表示.
例5已知数列{an}的前n项和为Sn,a1=1,an+1=2Sn(n∈N*),求{an}的通项公式.


∴an=2×3n-2(n≥2).

六、形如为常数




七﹑形如an+1=pan+qn+r(pq≠0),p,q,r为常数
这种题型可以设an+1+A(n+1)+B=p(an+An+B),对比前后两式,求出A,B,再化为等比数列求解.
例7设数列{an}:a1=4,an=3an-1+2n-1(n≥2),求an.
解设an+An+B=3[an-1+A(n-1)+B],则an+An+B=3an-1+3An-3A+3B,∴an=3an-1+2An+2B-3A.
∵an=3an-1+2n-1,∴A=1,B=1,
∴an+n+1=3[an-1+(n-1)+1].
又∵a1=4,∴a1+1+1=6,
∴数列{an+n+1}是首项为6,公比为3的等比数列.
∴an+n+1=6×3n-1,∴an=2×3n-n-1
八、形如
这种类型可以分类看看,若p=1,则等式两边取常用对数或自然对数,化为lgan=rlgan-1,得到首项为lga1,公比为r的等比数列{lgan},进一步求解即可;若p≠1,则等式两边取以p为底的对数得:logpan=rlogpan-1+1,可利用类型三求解.


∴{lgan}是首项为lg3,公比为2的等比数列.
∴lgan=2n-1lg3,
∴an=32n-1.
九、形如an+2=pan+1+qan,p,q为常数
这种题型可以把an+2=pan+1+qan化成an+2+λan+1=p(an+1+λan),求{an+1+λan}通项,再用类型三,类型四方法求解.


∵a1=1,a2=2,∴a2-a1=1.

∴an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)
以上为常见求数列通项公式的九种方法,其实数列通项公式的条件往往就有很强的指向性,只要把握好其中规律,结合方法总结,就可以对症下药,理清思路,这类型的问题就自然迎刃而解.

