关于多重共线性的三个知识点的准确表述

王义闹，卢庆华

(温州大学数理与电子信息工程学院，浙江温州 325035)

1 基本假定与基本结论

考虑多元线性回归问题，Y为被解释变量，X1,X2,…,Xk为解释变量，u是与解释变量无关的、方差为2σ的0均值随机干扰项，它们之间有如下关系：

其中β0,β1,β2,…,βk为常数．确定一组X1,X2,…,Xk的值Xi1,Xi2,…,Xik，重复试验、观察随机干扰下Y的值，可估计Y的（在X1=Xi1,X2=Xi2,…,Xk=Xik的条件下的条件）均值、方差、分布函数等．实际中我们更关心的是解释变量对被解释变量的净影响究竟有多大，即希望估计β0,β1,β2,…,βk，进而可对被解释变量进行预测、控制．假设在随机干扰值为ui时，观察到Y的值记为Yi：

假设ui是来自u的简单随机样本，且与Xi1,Xi2,…,Xik线性无关（或E(u|X)=0）．记

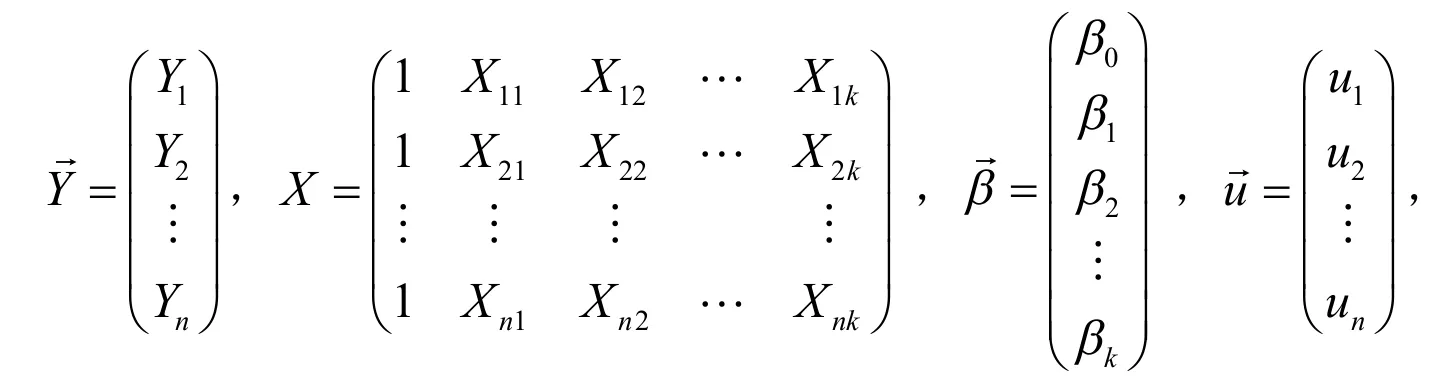
则（2）可表示成：

其中X称为回归设计矩阵或资料矩阵．为估计模型参数，以下设X是列满秩的．

模型参数的最小二乘（OLS）估计为：

其中为Xi对其它解释变量X0,X1,…,Xi-1,Xi+1,…,Xk回归所得决定系数，即Xi与其它解释变量X1,…,Xi-1,Xi+1,…,Xk的样本复相关系数Ri·的平方．

由（5）式可见，如果实验（观察）是可以人为设计（控制）的，则应该在Xi的离差平方和不变的条件下，使Xi与其它解释变量的样本复相关系数Ri·等于0，这样βi的OLS 估计的方差可以达到最小；否则，Xi的观察值列向量与设计矩阵X的其它各列之间的多重共线性越强，的方差越大．称为的方差扩大因子，记为VIFi．

本文在文[2]给出的下述（不完全）多重共线性定义基础上讨论．

定义1 当存在一个解释变量（不妨设为X1）与其它解释变量X2,…,Xk的样本复相关系数R1·大于0小于1 时，就称样本X（或设计矩阵X的列向量）存在（不完全）多重共线性，或称设计矩阵X的第2列与其它各列之间存在（不完全）多重共线性；当R1·=1时，就称样本X（或设计矩阵X的列向量）存在完全多重共线性，或称设计矩阵X的第2列与其它各列之间存在完全多重共线性；当R1·=0时，就称设计矩阵X的第2列与其它各列之间不存在多重共线性．

注：定义1 中的样本复相关系数R1·是以X1为被解释变量，以X0,X2,…,Xk为解释变量作普通最小二乘回归所得决定系数的算术根．

注意，当R1·=0时，设计矩阵X的第2列与其它各列之间不存在多重共线性，但其它各列中可能有某列与其余各列之间存在多重共线性，因此不能说设计矩阵X不存在多重共线性．

定义2 如果解释变量X1与其它解释变量的样本复相关系数为R1·，X2与其它解释变量的样本复相关系数为R2·，0＜R1·＜R2·＜1，则称设计矩阵X的第3 列与其它各列之间（比X的第2列与其它各列之间）存在较强多重共线性．对解释变量的两个样本X,X*，X1与其它解释变量的样本复相关系数为则称X*的第2列与其它各列之间（比X的第2列与其它各列之间）存在较强多重共线性．

以下假定设计矩阵X存在多重共线性．

2 参数的OLS估计值经济意义不合理的可能性较大

文[3]P112 所讲多重共线性的后果中有一个是“参数估计量经济意义不合理”：“如果模型中两个解释变量具有线性相关性，如X1和X2，那么它们中的一个变量可以由另一个表征．这时，X1和X2前的参数并不反映各自与被解释变量之间的结构关系，而是反映它们对被解释变量的共同影响，所以各自的参数已经失去了应有的经济含义，……”

以上讲法是不准确的．设定模型中X1和X2前的参数当然反映了各自对被解释变量的平均净影响，有特定的经济含义；有问题的不是X1和X2前的参数，而是参数的偏离真值特别远的估计值．当剔除X2后对保留变量用OLS 估计X1前的参数时，估计量是有偏的，估计值不仅反映了X1对被解释变量的影响，还包含了X2对被解释变量的部分影响，可以说“参数估计值经济意义不合理”．如果不剔除X2，X1和X2前的参数的OLS 估计量仍然是无偏的，只要估计值偏离真值不是特别远，就不能说“参数估计值经济意义不合理”．另外，说“参数估计量经济意义不合理”是没有特定意义的，参数所表示的“解释变量对被解释变量的平均净影响”是一个常数，而参数估计量是随机变量，所以无论设计矩阵X是否存在多重共线性，参数估计量经济意义都不合理．

确切地讲，应该是“参数的OLS 估计值经济意义不合理的可能性较大”．由于参数的OLS估计量仍然是参数的无偏估计，但方差较大，所以估计值偏离参数真值的可能性较大，当估计值偏离参数真值的幅度大到估计值与参数真值的正负号不同时，参数的OLS 估计值的经济意义就不合理了．

文[4]也存在类似问题．

3 作变量的显著性检验犯第二类错误的概率可能较大

文[3]P112 所讲多重共线性的后果中另一个是“变量的显著性检验失去意义”．

以XO表示第j列与其它各列之间不存在多重共线性的设计矩阵X，以XM表示存在多重共线性的设计矩阵X．在设计矩阵X取值为XO的条件下，对（3）式中随机干扰项的一个样本，由最小二乘法所得βj的估计量记为，则统计量在X取值为XO的条件下的条件分布是自由度为n-k-1 的t分布；在设计矩阵X取值为XM的条件下，对（3）式中随机干扰项的同一个样本，由最小二乘法所得βj的估计量记为，则统计量在X取值为XM的条件下的条件分布也是自由度为n-k- 1的t分布．所以不论设计矩阵X的取值是XO还是XM，在显著性水平α下拒绝原假设（H0:βj=0）犯错误的概率都是α，接受原假设（H0:βj=0）判断正确的概率都是1-α．因为假设检验通常是控制犯第一类错误（拒真错误）的概率，既然不论设计矩阵X的取值是XO还是XM，检验结果犯第一类错误（拒真错误）的概率都是α，就不能说“变量的显著性检验失去意义”．

文[4]也存在类似问题．

确切地讲，应该是：对原假设H0:βj=0，被择假设H1:βj≠ 0作t检验，与设计矩阵X的取值是XO的情况相比，X存在多重共线性时，尽管犯第一类错误的概率仍为α，但犯第二类错误的概率很可能较大．如果我们关注的是无关变量能否被剔除，则设计矩阵X是否存在多重共线性对检验结果没有影响；如果我们关注的是（与被解释变量）相关的变量能否被保留，则设计矩阵X存在严重多重共线性对检验结果有很大影响，条件允许的情况下应尽可能使设计矩阵X取XO；综合考虑的话，当然是X取XO最好．

下面对“犯第二类错误的概率很可能较大”这句话作简单说明．当真实情况是βj＞0时，t检验的原假设是H0:βj=0，接受原假设就犯了取伪错误．设计矩阵X取XO和X存在多重共线性的两种情况下接受域依次为：

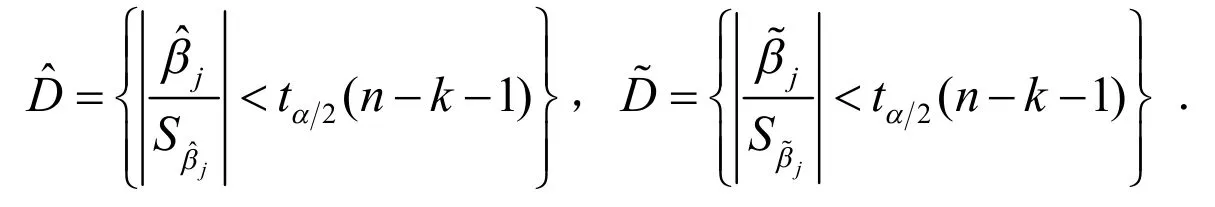
对随机干扰项的同一个样本，统计量都服从自由度为n-k-1的t分布，所以犯取伪错误的概率依次为：

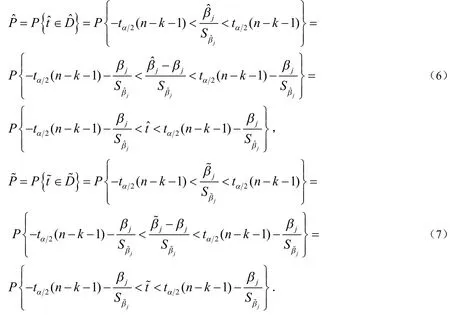
上式中的区间可以看成是(-tα/2(n-k-1),tα/2(n-k-1))向左平移得到的，平移幅度越大，概率越小．于是，若有

由（5）式可知，当我们对设计矩阵XO、存在多重共线性的设计矩阵XM，加上第j列离差平方和相等的限制时，就有：

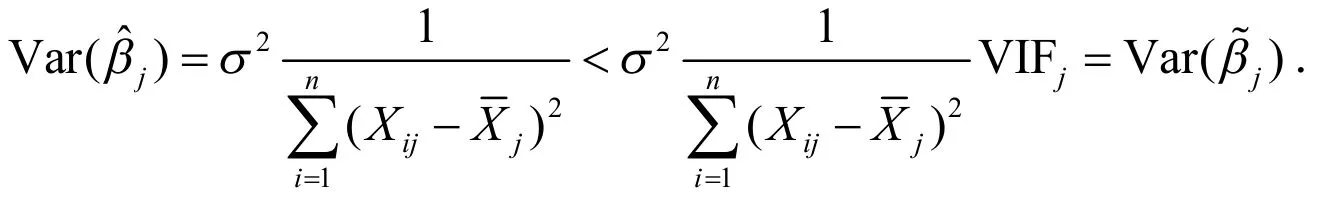
当真实情况是βj＜0时，有同样的结论：“犯第二类错误的概率很可能较大”．

设计矩阵X存在多重共线性时，作t检验犯第二类错误的概率，由（7）式可见随着真实βj取值不同而变化，可以综合考虑关于βj的先验信息和两类犯错误概率做出取舍．

文[5]P329 第一、二两行讲述了的多重共线性的一个实际后果：“在高度多重共线性的情形中，样本可能与分歧很大的一些假设均无矛盾，这样就增加了接受错误假设（即犯第Ⅱ类错误）的概率．”由本文上述讨论可见，把“就增加了接受错误假设的概率”添加三个字“很可能”，改为“就很可能增加接受错误假设的概率”是更稳妥的表述．

文[5]P329 第五、六两行讲到：“在高度共线性情形中，估计的标准误增加奇快，从而t值迅速变小．”这样讲容易让读者产生误解．由本文上述讨论可见，当原假设（H0:βj=0）成立时，都服从自由度为n-k-1 的t分布，所以不会对的任一观察值都有当被择假设（H1:βj≠ 0）成立时，的概率很大（但也不是必然成立）．

文[6]P193、文[7]P101 存在与文[5]P329 第五、六两行同样的问题．

4 剔除相关变量有可能减小保留参数的OLS估计的方差

文[8]在讲解对多重共线性问题的补救时讲到：“如果发现多元线性回归模型存在严重的多重共线性，则应利用相应的补救措施来最小化多重共线性所造成的影响．”本文十分赞同这句话，认为解决多重共线性问题，基本假定是存在多重共线性的多元线性回归模型就是我们所研究的问题的真实规律，目标是尽可能减小多重共线性对我们认识问题、分析问题所造成的不利影响．文[8]紧接着说，剔除变量法是消除多重共线性最简单的一种方法．文[3]在P114 讲解克服多重共线性的方法时讲到：“找出引起多重共线性的解释变量，将它排除出去，是最有效克服多重共线性的方法，所以逐步回归法得到了最为广泛的应用．”

实际上，如果我们要分析“控制单个随机解释变量的条件下被解释变量的平均改变量”[9]E(Y|Xi=xi1)-E(Y|Xi=xi0)，则剔除相关变量，然后对保留变量系数用OLS 估计，所得估计量恰好是我们要求的平均改变量的无偏估计、一致估计．

如果我们要分析“保持其它解释变量不变，且Xi增加一个单位的条件下，被解释变量的平均改变量”，就要求尽可能准确地估计Xi的系数βi．这时，剔除相关变量，然后对保留变量系数用OLS 估计，βi的估计量的均方误差有可能小于等于对全部变量系数直接用OLS 估计所得βi的估计量的均方误差．“小于等于”成立的条件是，对全部变量系数直接用OLS 估计所得被剔除变量的估计量的协方差阵，减去被剔除变量系数真值构成的列向量与其转置乘积矩阵，是一半正定矩阵．详见文[9]定理2.2．

如果要对解释变量取某组值时被解释变量的取值进行预测，先剔除相关变量，然后对保留变量系数用OLS 估计，进而用保留变量作预测的均方误差有可能小于等于对全部变量系数直接用OLS 估计进而作预测的均方误差．“小于等于”成立的条件与上段相同．详见文[9]定理2.5．

综合以上三种情况可见，对不同的分析目标、分析要求，剔除引起多重共线性的解释变量，可能减小多重共线性所造成的影响，也可能得到更差的结果．笼统地说“找出引起多重共线性的解释变量，将它排除出去，是最有效克服多重共线性的方法”，是不恰当的．