面向多模态图像的柯西相关特征学习方法

苏树智,谢 军,高鹏连,邓瀛灏,郑 苹

(安徽理工大学 计算机科学与工程学院, 安徽 淮南 232001)

根据图像数据来源的数量，图像可以分为单模态图像和多模态图像[1]。单模态图像是同一目标仅有一类图像进行描述。目前，面向图像的特征学习方法主要集中在单模态图像，其中主成分分析[2]、线性鉴别分析[3]和局部保持投影[4]是最具代表性的单模态特征学习方法，这些方法在遥感图像处理、机器人定位、基因数据分析、核磁共振数据分析等实际应用中已经取得成功。多模态图像的本质是同一目标拥有两类或两类以上的图像[5]，比如借助不同的图像采集设备能够同时获得某个人的可见光图像、近红外图像以及热红外图像等等。这些图像可以从不同的角度描述同一个人的多种统计信息，并且具有互补性，通常被称为这个人的多模态图像。多模态图像可视为描述同一目标的单模态图像的集合，比单模态数据拥有更加丰富的信息，然而如何从多模态图像中学习有效特征仍然是一个亟待解决的问题。

从多模态图像中学习低维特征的常用方法[6]是利用串联策略，将多模态图像数据转化为单模态图像数据，然后再借助单模态特征学习方法进行低维特征的学习。尽管这种方法经常能够有效增强识别或分类的性能，然而同样也拥有明显的缺点，比如数据的维数会急剧增加，使计算时间和存储空间大幅提高，甚至会造成采集的数据量远小于数据的维数，进而严重影响分类器的泛化能力[7]。针对该问题，很多学者从不同模态间的互补性和相关性出发，提出了一些多模态特征学习方法。局部排列的多模态特征方法[8]能够从多模态图像中学习一种鉴别潜在子空间，该子空间尽量保留了原始高维数据的局部几何结构，使子空间投影后的低维特征更具鉴别力。借助广义模态均值，多视图鉴别分析方法[9]能够从多模态数据中学习低维鉴别特征，该特征尽量保留了模态间和模态内的鉴别散布信息，具有良好的鉴别力，并在图像识别中验证了方法的有效性。为了掌握多模态数据的内在结构，Zhao等[10]构建了一种最大粒度结构描述因子，能够抽取多模态数据的局部显著特征，并在此基础上形成基于数据一致性的广义多模态特征学习方法。

典型相关分析(canonical correlation analysis，CCA)[11]是一种重要的多模态特征学习方法。该方法旨在学习两模态数据的一致子空间，使原始高维数据投影到一致子空间后，模态间拥有最大的相关性。目前，CCA在很多实际应用中已经广泛应用，比如故障检测[12]、多模态生物分析[13]以及过程监控[14]。CCA本身是一种线性方法，这使其难以很好地掌握数据中隐含的非线性结构信息。局部保持CCA(LPCCA)[15]构建了局部模态间相关优化问题，通过求解该优化问题，能够进一步获得非线性相关特征，并在人脸的姿态估计中验证了方法的有效性。核技术是一类常见的非线性辅助技术，将核技术与CCA有效融合，进一步形成了核CCA(KCCA)[16]方法。该方法首先利用高斯核函数将原始高维数据映射到更高维的核空间，使原始高维数据具有高维可分性，然后再在核空间中执行相关特征的学习。CCA学习的相关投影方向不具有正交性，因此CCA的相关特征难以最大限度地消除冗余。为此，正交CCA(OCCA)方法[17]通过在CCA的目标函数中添加正交约束，构建了正交相关优化问题，学习了正交的相关投影方向，进一步获得了“稠密”的相关特征。CCA的无监督性在很大程度上限制了相关特征的鉴别力。为此，Gao等[18]学习了鉴别相关特征，并在图像表情识别中验证了方法的有效性。

上述所有方法都涉及基于样本数据的协方差矩阵，即样本协方差矩阵。由于实际应用中采集的样本往往包含大量的冗余和噪声信息，样本协方差矩阵通常偏离真实协方差矩阵。对于特征学习方法，样本协方差矩阵越接近真实协方差矩阵，特征学习方法获得的特征往往具有越好的鉴别力[7]。为了解决样本协方差矩阵偏离的问题，本文利用柯西估计对协方差矩阵的奇异值进行纠正，进而形成一种更加接近真实协方差矩阵的柯西协方差矩阵，然后在相关分析理论的基础上，进一步提出面型多模态图像的柯西相关特征学习方法，即柯西典型相关分析(Cauchy canonical correlation，简写为CauCCA)。该方法能够同时从不同的模态学习具有强鉴别力的相关特征。为了分析方法的有效性，在3个常用的图像数据上设计了针对性实验，良好的实验结果已经显示该方法是一种有效的多模态图像识别方法。

1 柯西典型相关分析方法

1.1 协方差矩阵的讨论

协方差矩阵对于特征学习的方法性能至关重要。由于在实际应用中难以获得真实协方差矩阵，通常利用样本协方差矩阵来逼近真实协方差矩阵，然而样本的冗余和噪声信息会导致样本协方差矩阵的偏离。为了衡量样本协方差矩阵和真实协方差矩阵的偏离，定义了协方差矩阵的偏离度θ:

(1)

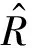
图1 不同样本数量对应的偏离度

图2 不同样本维数对应的偏离度

1.2 柯西协方差矩阵

假设X=[x1,x2,…,xN,]∈Rdx×N和Y=[y1,y2,…,yN]∈Rdy×N是对应相同目标的两个模态数据集。其中(xk,yk)是对应同一目标的第k(k=1,2,…,N)对样本，N为样本数量，dx和dy分别表示模态数据集X和Y的样本维数。

对于模态数据集X和Y，模态内样本协方差矩阵的定义是相同的。下面以模态数据X为例，描述如何纠正模态内样本协方差矩阵的奇异值，进而形成更接近真实协方差矩阵的柯西协方差矩阵。模态内样本协方差Rxx的定义为

(2)

R(xx)=P(xx)Λ(xx)Q(xx)T

(3)

(4)

(5)

利用柯西估计对样本协方差矩阵的奇异值进行纠正是一种减少样本协方差矩阵偏离度的全新思路，能够有效提升很多特征学习方法的鉴别力。

1.3 柯西协方差矩阵的分析

图1和图2除了展示样本协方差矩阵的偏离度以外，还直观地展示了柯西协方差矩阵随样本数量和样本维数增加的变化趋势。从图1和图2可以看出：随着样本数量的增加和样本维数的减少，柯西协方差矩阵的偏离度呈现减小的趋势，并且和样本协方差矩阵相比，柯西协方差矩阵总是更接近真实协方差矩阵。

为了深入分析柯西协方差矩阵更接近真实协方差矩阵的原因，将真实协方差矩阵、样本协方差矩阵以及柯西协方差矩阵进行奇异值分解，然后将奇异值分别进行从大到小的排列，并在图3中展示了排序后的奇异值。从图3可以看出：柯西协方差矩阵对奇异值进行了纠正，纠正的奇异值更接近真实协方差矩阵的奇异值，这是柯西协方差矩阵更接近真实协方差矩阵的重要原因。

图3 真实协方差矩阵、样本协方差矩阵和柯西协方差矩阵的奇异值

1.4 柯西典型相关分析

假设α∈Rdx×1和β∈Rdy×1分别是模态数据X和Y对应的相关投影方向，αTX和βTY为投影后的相关特征。柯西典型相关分析(CauCCA)旨在学习使模态间相关性最大的相关投影方向，因此，借助相关准则[11]，CauCCA的相关优化函数能够表述为

(6)

由于α和β具有尺度不变性[17]，式(6)能等价地转化为下面的优化问题：

(7)

借助Lagrange乘子法[19]，可以构建式(7)的Lagrange乘子函数L(α,β):

(8)

其中η1和η2是Lagrange乘子。通过将L(α,β)对α和β的偏导数设为零，可得：

(9)

(10)

式(9)左乘αT和式(10)左乘βT，可得：

(11)

(12)

(13)

(14)

经过简单的推导，式(13)和式(14)能等价地转化为下面的广义特征值问题：

(15)

(16)

(17)

CauCCA方法输入:模态数据集X=[x1,x2,…,xN]∈Rdx×N;模态数据集Y=[y1,y2,…,yN)]∈Rdy×N输出:相关投影矩阵A和B1. 利用式(4)构建模态内柯西协方差矩阵R(xx)Cau和R(yy)Cau;2. 利用式(5)构建模态间柯西协方差矩阵R(xy)Cau;3. 求解式(15)和式(16)即可获得相关投影矩阵A和B

对于最终的识别任务，不同模态的相关特征需要进行融合。假设{x,y}为对应同一目标的训练样本或测试样本，则可以借助简单的融合策略[6]获得{x,y}的融合相关特征z：

z=ATx+BTy

(18)

2 实验结果及其分析

为了评估提出方法的有效性，在GT图像数据集(http://www.anefian.com/research/face_reco.htm)、AT&T图像数据集(http://www.cad.zju.edu.cn/home/dengcai/Data/FaceData.htm)以及IRIS热红外/可见光图像数据集(http://vcipl-okstate.org/pbvs/bench/)上进行了实验。GT数据集和AT&T数据集属于单模态图像数集，为此借助模态策略[19]获取每幅图像的两种模态数据。具体而言，利用Coiflets和Daubechies小波变换方法来获取每幅图像的两个模态数据，随后使用主成分分析将模态数据的维数约减到100维，以减少小样本问题。IRIS数据集利用不同的图像设备采集了同一目标的热红外图像和可见光图像，是常用的两模态图像数集。借助模态策略中小样本问题的处理方法，IRIS数据集同样也利用主成分分析将模态数据的维数约减到100维。

表1 在GT图像数据集上的平均识别率 %

参数4Train5Train6Train7TrainCauCCA67.8071.9073.6077.00OCCA65.9169.1670.8473.88KCCA66.2270.8872.5374.93CCA52.8059.0861.7866.22

表2 在AT&T图像数据集上的平均识别率 %

参数4Train5Train6Train7TrainCauCCA93.6795.6597.7597.75OCCA93.6296.3097.4497.50KCCA78.3890.3593.1993.83CCA92.2994.7596.5097.17

表3 在IRIS热红外/可见光图像数据集上的平均识别率 %

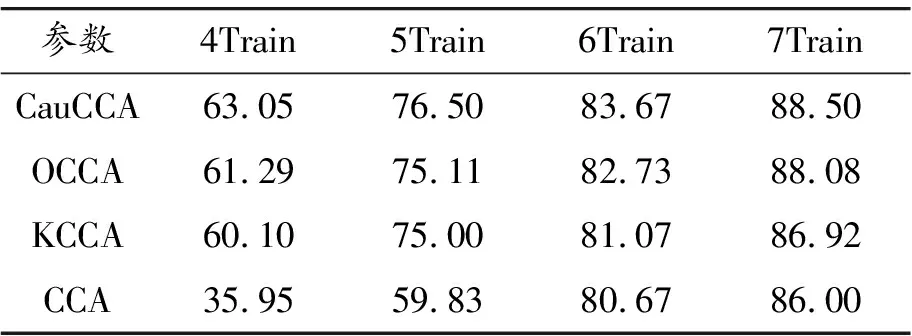
参数4Train5Train6Train7TrainCauCCA63.0576.5083.6788.50OCCA61.2975.1182.7388.08KCCA60.1075.0081.0786.92CCA35.9559.8380.6786.00

在实验部分，将CauCCA与OCCA、KCCA以及CCA进行了对比分析。该方法中的参数c从数据间隔为0.1的[0.1,1]区间内以及数据间隔为1的[2,10]区间内，利用交叉验证寻找最优参数。在最终的识别任务中，分类器使用的是基于欧式距离的最近邻分类器，并且展示了所有可能维数下的最优识别率。在3个图像数据集上，随机从每类中选择u(u=4,5,6,7)幅图像作为训练图像，剩余图像用于测试，独立运行10次样本随机实验，在表1～3中分别展示了平均识别率。

图像数据是一种常见的高维小样本数据，即数据维数高，样本数量相对较少。从图1、2可以看出，基于图像数据的样本协方差矩阵往往严重偏离真实协方差矩阵，这是CCA在3个图像数集上拥有较差识别性能的重要原因。然而CauCCA利用柯西估计对样本协方差矩阵的奇异值进行了纠正，构建了更接近真实协方差矩阵的柯西协方差矩阵，进而有效增强了相关特征的鉴别力，并在表1～3中分别显示出了良好的识别性能。CauCCA在识别率上明显优于CCA，这进一步验证了对柯西协方差矩阵分析的正确性。OCCA在相关投影的优化问题中添加了正交约束，并在理论上提升了数据压缩的紧凑性，最大限度地减少了相关特征的冗余信息。该方法在图像识别中也显示了相对较好的识别性能，在一定程度上改善了相关特征的鉴别力。KCCA利用经验核函数探索了原始高维数据中隐含的非线性结构信息，然而由于经验核函数不具有数据适应性，KCCA难以在各类数据集上很好地揭示数据的非线性结构，这是KCCA在3个不同数据集上相对识别性能相差较大的重要原因。OCCA和KCCA是相关特征学习中的两类代表性方法，该方法在大多数情况下拥有比OCCA和KCCA更高的识别率，这在一定程度上也显示了CauCCA在图像识别中的有效性。此外，OCCA和KCCA也是基于协方差矩阵的相关特征学习方法，利用CauCCA构建的柯西协方差矩阵，同样能够进一步增强OCCA和KCCA的识别性能。

3 结束语

在实际应用中难以直接获得真实协方差矩阵，基于协方差矩阵的特征学习方法通常是利用样本协方差矩阵来逼近真实协方差矩阵，然而由于实际采集的样本包含大量的冗余和噪声信息，样本协方差矩阵往往严重偏离真实协方差矩阵，进而影响特征学习的方法性能。为了从样本数据获得更加真实的协方差矩阵，首先对样本协方差矩阵进行奇异值分解，并利用柯西估计纠正样本协方差矩阵的奇异值，进而获得更接近真实协方差矩阵的柯西协方差矩阵，然后结合相关分析理论，提出面向多模态图像的CauCCA方法，该方法能够从少量图像中学习强鉴别力的相关特征。在3个常用的图像数据集上设计了针对性实验，实验结果显示CauCCA是一种有效的图像识别方法。在理论上，基于协方差矩阵的特征学习方法能够借助柯西协方差矩阵的优势进一步提升方法性能。如何将柯西协方差矩阵有效嵌入其他特征学习方法，以及嵌入柯西协方差矩阵后特征学习性能的改善程度将是进一步研究的重点。