丢番图方程x2+4=8y11的整数解

高 丽，焦龙强

(延安大学 数学与计算机科学学院，陕西 延安 716000)

丢番图方程x2+A=Dyn(A,D∈N,n≡1(mod2))属于Ramanujian-Nagell类方程，关于它的整数解问题，目前已经有很多的数学爱好者对它进行了研究。

legendre[1]证明了当A=1,D=1时，方程x2+1=yn无整数解；黄勇庆[2]证明了当A=4,D=1,n=3时，方程x2+4=y3无整数解；张四保[3]证明了当A=42,D=1,n=13时，方程x2+42=y13无整数解；高丽，马永刚[4]证明了当A=42,D=1,n=7时，方程x2+16=y7无整数解；李中恢，张四保[5]证明了当A=16，D=1，n=11时，方程x2+16=y11无整数解；许宏鑫[6]等证明了当A=44,D=1,n=9时，方程x2+44=y9仅有整数解(x,y)=(±16,2)；冉银霞[7]证明了当A=43,D=1,n=7时，方程x2+43=y7仅有整数解(x,y)=(±8,2)；王振，张慧[8]证明了当A=4n(n≥3),D=1时，方程x2+4n=y3(n∈N,x≡0(mod2),x,y∈Z,n≥3)整数解仅有(x,y,n)=(0,4k,3k),(±2×8k,2×4k,3k+1),(±11×8k,5×4k,3k+1),k∈N*。

本文主要讨论了当A=4,D=8,n=11时，丢番图方程x2+4=8y11的整数解的问题。

1 预备引理

引理1[9]Z[i]中1+i的部分性质：

(1)(1+i)2=2i,(1=i)4=-4,

(1-i)i=1+i；

(2)1+i|a+bi当且仅当2|a+b；

(3)如果1+i⫮a+bi，那么

(a+bi)2≡±1(mod4)。

引理2[10]设M是唯一分解整数环，正整数k≥2，α,β∈M，(α,β)=1，那么，若αβ=γk，γ∈M，则有α=ε1μk，β=ε2vk，μ,v∈M，其中ε1，ε2，是M中的单位元素，并且ε1ε2=εk，ε为单位元素。

2 定理及证明

定理丢番图方程

x2+4=8y11(x,y∈Z)

仅有整数解(x,y)=(±2,1)。

证明：分两种情况：x≡1(mod2)，x≡0(mod2)。

(1)x≡1(mod2)时：则在Z[i]中，(1)式可以等价写成：(x+2i)(x-2i)=8y11，x,y∈Z。

设δ=(x+2i,x-2i)，由δ|(2x,4i)=2得，由引理1得δ只能取值1，1+i，2。

因为x≡1(mod2)，有x+2i≡1(mod2)。

所以δ≠2。

假设δ=1+i，有N(1+i)|N(x+2i)，即2|x2+4，x≡0(mod2)，与x≡1(mod2)矛盾，所以δ≠1+i。

所以必有δ=1。

由引理2可得：x+2i=8(a+bi)11，

化简上式得：

x=8(a11-55a9b2+330a7b4-462a5b6+

165a3b8-11ab10，

1=2b(11a10-165a8b2+462a6b4-330a4b6+

55a2b8-b10)。

因为b∈Z，由上面第二式可得b没有可能的取值。

所以当x≡1(mod2)时，丢番图方程x2+4=8y11无整数解。

(2)x≡0(mod2)时：可知x为偶数，设x=2x1(x∈Z)；代入到原方程式可得：(2x1)2+4=8y11，化简得：x12+1=2y11。

由上式可知，x1为奇数，只需讨论x12+1=2y11的整数解问题。

因为x1是奇数，则在Z[i]中方程x12+1=2y11可以写成：

(x+i)(x-i)=i(1-i)2y11。

设μ=(x+i,x-i)，则μ|(2x,2i)=2，可知μ可以取值1，1-i，2。

当μ=1时，i(1-i)2=2一定只能整除x1+i，x1-i中的一个，因为x1是奇数，所以不可能，即μ≠1。

所以μ=1-i，由此可得：

由引理2可得：x1+i=(1+i)(a+bi)11。

因此有：

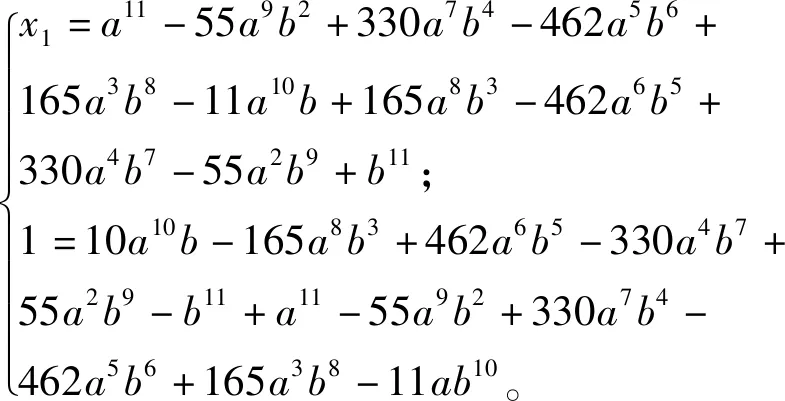
由上式可得a=0，b=±1，x1=±1。

即x=±2，y=1。此时方程有整数解(x,y)=(±2，1)。

综上所述，丢番图方程x2+4=8y11(x,y∈Z)仅有整数解(x,y)=(±2,1)。