《割圆密率捷法》中的奇零尾数问题

王鑫义

（内蒙古师范大学科学技术史研究院，内蒙古呼和浩特010022）

中国古代分数理论较之小数理论有着悠久的历史和卓越的贡献。中算书中的数一般由“全”和“分”两部分构成，中算家称整数部分为“全”，奇零部分为“分”[1]。古代典籍中常用“奇”、“有奇”、“余”、“有余”等词语来表述奇零小数[2]，有用“强”、“弱”、“微强”等来表示的，其中都蕴含了奇零尾数的处理方法，一般用“四舍五入”，也有用去尾就整的方法，有时也将奇零尾数在可能范围内多化为分数，并将各分数的分母化为近似的公分母，以求整齐划一。刘徽已对小数有深刻认识，且已认识到不尽方根不能用十进小数的有限形式来表示。《数理精蕴》中用“小余”、“有余”等表述奇零问题。尽管中国古代数学中并未明确提出过有理数、无理数的概念，但“奇零小余”中却包含着有理数和无理数两种情形，若“奇零小余”是有限小数或无限循环小数，则“奇零小余”为有理数；若“奇零小余”是无限不循环小数，则为无理数[3]。

《割圆密率捷法》（以下称《捷法》）中有多处涉及到奇零尾数的近似计算问题，因后三卷中出现的奇零尾数问题有所不同，选取后三卷中的部分典型案例，分别讨论明安图对奇零尾数的处理情况，对出现的不同题型中采用相同方法的问题将不再重复分析。

1 卷二中的奇零尾数问题

卷二中用无穷级数展开式进行天文计算，出现了对每条数的奇零尾数处理问题和对部分条数的舍弃问题，明安图采用截断法和进一法，在原有数字后多保留一位数字，作为安全数字或参考数字，当所参与运算的条数成为纯小数时，便将其和其后面的条数都舍去不求。以卷二中具有代表性的角度求八线问题为例来说明：

“以周天度化为一百二十九万六千秒为一率，倍圆周定率，得六千二百八十三万一千八百五十三，为二率；设度化为一十五万六千一百一十秒，为三率；乘除得四率七百五十六万八千四百二十六，小余三。带小余一位单位数方密，后仿此。……，第五条数止一位，第六条数必在小余下，故可省求。置右总数减左总数，得六百八十六万六千二百九十五，小余七，进为一。第二条得数仅二位，而比第一条数降四位，则第三条数必降至奇零下，即无庸求。”[4]

明安图用放大半径之法，取半径为一千万（107），显然，给定半径的位数越多，尾数将越精确。圆周率以3.141 592 65 入算，再将圆周角360度化为1 296 000秒，转化方法与现在一样，通过计算得到各条数的近似值。下面求得相对误差，并做简要分析：

在卷二的实际应用问题中，明安图做加减运算时，为使参与计算的个位数和最后的结果有尽可能高的精度，他要求所有参与运算的数字，均保留一位小数参加计算。表1中计算出的相对误差值为Ei（i=1，…，6），只有E6偏大以外，其它的相对误差值都较小，Ei在逐渐增大，用U来表示求未知量时累积的相对误差值，U=E1+…+E6，事实上，在放大半径计算时所累积的相对误差U是允许的。从表1中的近似值与精确值来看，舍去的部分最前面的数字大于5的却没向上进一位，如出现的6和7，舍去的部分最前面的数字小于5的直接舍去，如出现的1、2和4，因而他在这里采取的是截断法，即简单地截去第一位小数位数以后的数字而得到所需结果。从第五条开始，近似值和精确值越来越小，造成的相对误差会越来越大，“第六条数必在小余下，故可省求”，即第六条已变成了纯小数，因而从第六条开始不再计算直接舍去，这也是化繁为简的一种做法。

而表2中明安图是用“进为一”的方法得到的近似值，卷二中还有几处的最后结果采取的也是此法，“进为一”即进一法，如：求得的小数点后的一位数字分别为7 和9，他采用进一法将前一位加1。这里处理奇零尾数采用的并非四舍五入方法，对“不过半（或不过5）”的情形是否也采用进一法来处理，原文中并未说明。求得前四条后，他已意识到每次得数减少两位，第四条数还有三位，须求第五条，而第五条数字只有一位，第六条已成为了纯小数，从第六条开始舍去不求，并通过降位，在求得第一、二条数后，发现第二条数仅有两位，比第一条数减少了四位，得出第三条数一定减少到小数，他认为对于降到奇零下的条数对整个运算结果没有太大影响，故不再计算直接舍去，说明他对计算结果的变化规律已有了很清楚地判断。

若e的近似值e*的规格化形式：

e*=±0.a1a2···an×10m（a1,a2,···,an都为 0～9中的任一数字，a1≠0 ，n是正整数，m是整数）有n位有效数字，则相对误差限为：

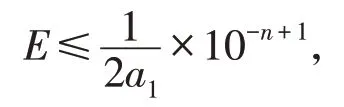
说明e*的有效数字位数越多，其相对误差限也越小，《捷法》中明安图给出的有效数字的位数能深刻反映近似值的相对精确度。

在已知角度求八线中，明安图用多项式：

近似代替弧背求正弦公式：

x用弧度表示，n≥1，弧背求正弦公式满足莱布尼兹准则[5]，为莱布尼兹级数，截断误差为：

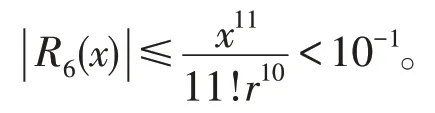
说明从第六条开始只有“分”没有“全”，舍去第五条以后的实质即为此。虽终止于第六条将会出现误差，明安图也没有考虑如何避免数值误差，但对于取较大整数作为半径计算时，只需取一些项，且这些项的数值大小是递减的，直到任何一步误差大小的数量级等于丢掉的第一项大小的数量级[6]。

在多个数求和时，被加数的绝对值之间相差较多，且后面包含许多绝对值较小的数，若要缩小相对误差，提高精度的最直接有效的办法就是增加各项数值的有效位数，但它同时增加了计算量。“带小余一位单位数方密”，即保留一位小数，增加一位有效数字，使计算结果更精密，说明他对误差已有一定的认识。

2 卷三中的奇零尾数问题

2.1 “分弧通弦率数求全弧通弦率数”中的奇零尾数问题

“分弧通弦率数求全弧通弦率数”中出现不足法和十五率后截去不用的问题。被除数的绝对值小于除数的绝对值，各率的被除数的绝对值比除数的绝对值减少得快，则比值会越来越小且前后两项的比值会越来越接近，防止参与运算的数在数量级上相差悬殊，明安图采用截断法，即仅保留无穷过程的前段有限项而舍弃它的后段。

“十一率、十三率皆不足法，于各率上加一分母十六。……。十五率后截去不用，故求至十五率止。盖连比例至十五率为数已密。”[4]

明安图求得十一率、十三率时不够除，被除数的绝对值小于除数的绝对值，得到十五率后，指出十五率后截去不用。事实上，他也是考虑到十五率以后“不足法”，被除数的绝对值与除数的绝对值会越来越不够除，绝对值很小的数作了被除数，即在计算y/x时，若0＜|y|＜＜|x|，在整个的计算过程中，就会出现前后两个相近的数相减和前面的大数“吃掉（淹没）”后面的小数的现象。明安图采取截断法只取了前七项，“十五率后截去不用”，因不能精确计算得到无穷多项的和或差，故只能截取有限项来计算。在具体计算时，他已清除地认识到只能对有限项数进行有限次运算，故截断了无穷过程。

由有限过程逼近一个无限过程实质上是在求解一个近似问题，他把无限的计算过程用有限的计算过程代替，求解时必定会产生截断误差。当分子不太小时，近似计算的误差主要取决于截断误差，从理论上看，分子越小，截断误差也越小，逼近程度应该越好，分子很小时，截断误差将变得微乎其微，故当分子充分小时，涉及前后两个相近的数相加减，以防有效数字损失，可用有限项的值近似代替无限项的值，用有限过程逼近无限过程，用能计算的问题代替不能计算的问题。他认识到了截断误差问题，却没有严格控制住在计算过程中所造成的累积的截断误差。

2.2 “弧背求通弦率数法解”中的奇零尾数问题

由于弧线与直线不能达到同一，“弧背求通弦率数法解”中总有奇零数不能整除的问题。明安图继承并发挥了自刘徽以来的极限思想，认为“去奇零而用整分”是弧与直线达到同一的最佳途径。

“置千分弧四率分数，四归之，为应减四率数，为法。法除实，得二十四分〇〇〇〇二四不尽，是全四率亦为应减四率之二十四倍有余。……。夫二十四分之数不改，惟奇零之差逼弧愈近则愈微。若径以弧背为二率，则奇零必尽，而为二十四分整数矣。盖累求而奇零不尽者，此弧线、直线之所以不可一也；去奇零而用整分者，因其不可一而得其所以可一也。”[4]

明安图在研究弦与弧的无穷逼近问题时，指出在无穷分割的条件下，曲线和直线可以达到同一。首先用百分、千分、万分弧的共用二率数作为二率来求各率分数，求四率分数时，先以百分弧二率共用数依次求得三、四率数，再以四率率数106为被除数，166650/4=41662.5 为除数，相除后为24.00240024，其中小数点后的0024为除之不尽的数。同样的，以万分弧二率共用数计算时，得到24.00000024，其中小数点后的00000024 为除之不尽的数，相比千分弧就更小了。原著中相当于做了如下计算：

“二十四分之数不改，惟奇零之差逼弧愈近则愈微。”即阐明了计算所得到的各数值的整数部分为24是一定的，只有小数部分在不断变化，而且奇零差数越逼近圆弧变得越加微小，整数与小数部分相差越来越大。这与后面整数部分出现的80、168、288等实质是相同的，所采用的方法都是“去奇零而用整分”，由于实际的需要将位数较多的数字近似地写成了位数较少的数字，弧线与直线相同一的方法则是采用去尾法把奇零尾数直接舍去而用整数，即整化[7]。当角度越小，分割越细时，需要调整系数，通过计算得到的数值的整数部分来近似代替无穷级数展开式的各项系数的分母。由于被除数、除数数字庞大，做近似计算截去了末尾若干位数字，即去尾就整，虽然计算有所简便，但减少了有效数字的位数，一定程度上损失了结果的精度。原著中在进行相当于求极限的近似计算时，以曲直异同说作为理论基础，虽然当弦逐步变小时并非严格意义上的无穷小概念，但为有限走向无限做了很好的铺垫。将无限过程通过运算合理地表达了出来，形象地描述了弦弧互化的过程，但缺乏分析的讨论，并非严格意义上的证明。

3 卷四“弧背求正矢率数法解”中的奇零尾数问题

由于原著中的数字单位较大，数字到一定位数后末尾的0 较多，明安图采取的是截断法，即简单地截去被除数和除数的末尾含有0的相同位数，避免了计算时造成的干扰，保证了得数的准确性[8]。

“求五率分数，…，次置万分弧三率共分数，以三率乘之，得五率分数二分之一京，为实。入算截去末六位。置万分弧五率共分数一六六六六六六六五〇截去末六位，二归之，得数八三三三三三三二五，为法。…。求七率分数，…，截去后七位，…，截去后十三位。…，求九率分数，…，截去后四位，…，截去后六位，…，截去后十二位，…，截去后二十位。…。求十七率分数，…，截去后四十四位。”[4]

明安图所使用的数字单位中有一[9]，有京[10-11]等，其中的大数远远超过了实际需要。特别是整数与小数部分相差较大时，计算量十分繁重，算至多位以后，小数部分越来越小，要使演算继续进行下去，可代之以简单分数的办法，这无疑简化了对数据的调整手续，这也是作为一种方法在当时长期使用的价值所在[12]。取半径一千万代替单位圆具有极好的“放大”作用，这种高倍“放大”，改进了数值精度。当无限分割后，不尽之数越来越小，直至奇零消去，如，求七率时截去了被除数和除数的末尾七位（00012 为除之不尽的数）、十三位（0000012 为除之不尽的数），等等，后面各率数的被除数和除数的末尾都做了相应地处理，并将各率系数的分母写成连续两数乘积的形式，如：

2×12×30×56×90×132×···=

1×2×3×4×5×6×7×8×9×10×11×12×···

现今无穷级数各项系数的分母都写成阶乘的形式，如：2!，4！，6！，8！，…。将原著中被除数（记为A）和除数（记为B）规范为下面的形式：

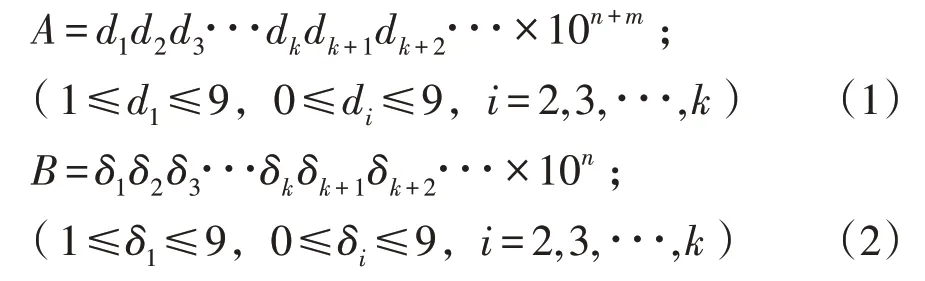
原著中相当于进行了如下计算：

将每个数据都用有限位的数字表示，用有限位小数代替无穷位小数。他认为，在一个数值中小数点后面的位数越多，这个数值并不一定会越精确，或者在具体运算中保留的位数越多，精度并不一定会越高，写得更精确是没有意义的。这里所用的截断法与前面的截断法是不同的，前面所使用的截断法针对的是项数而不是数字，在（3）式的处理中，他认为可同时适当截去若干位数字，只保留入算的部分，不仅简化计算，且不影响所需精度。

4 结论

明安图在处理奇零尾数时，对奇零尾数的取舍不是随意的，而是有一定原则的，采用截断、进一、去尾等方法简化了计算程序，并对造成的误差有一定的认识。他大量采用截断法，截断的原则是把所要求达到的精度那一位（项）以后的数字（项）弃去或截断，按截断原则确定需要截断到哪一位（项），再按截断法加以处理，这样便得到一个恰到好处的近似值。对“过半（或过5）”的情形采用进一法，弧弦互化的时候则采用去尾法以达到整化的目的。用级数公式本就是做了近似逼近计算，将奇零尾数又做了近似取值或取舍，将会产生更大的误差。可以看到，他在《捷法》中大量的计算更多的是为说明无穷级数展开式可以快捷方便地解决一类繁琐复杂的问题，是以解决问题为最终目标，突出方法的创新，因而他并未对结果的精确度有过多的要求。他虽未严格控制所采用的奇零尾数处理方法所带来的相应误差，但他所采用的处理方法是对新问题进行的新思考所用的新方法，这种处理奇零尾数的方法，在现今的分析学中亦可资借鉴。