基于微课的微专题设计分析
吴俊英


[摘 要] 文章以空间中平行与垂直为例,阐述微专题在复习课中的应用模式.精选例题及测试题,用微型精细化原则将有关空间的平行与垂直分割成“小切口”的6个微专题,通过例题及变式练习,落实直观想象素养与数学运算素养的培养,最后给出结合利用微课进行微专题教学实践的建议.
[关键词] 微课;微专题;平行与垂直;直观想象
■引言
立体几何在高考考查中一般占据22分,其题型与题量一般是1个解答题,1~2个选择题或填空题.高考中立体几何的解答题常以棱柱或棱锥为载体,解答题一般采用分步设问的方式,常见的两个考查热点:一是定性分析,二是定量分析. 其中定性分析,文科主要是以平行、垂直的证明为主;而定量分析,文科试题主要考查表面积、体积的计算. 经过高三一轮复习,学生已经学习了直线、平面平行垂直的判定及其性质,对空间概念有一定的基础. 但是,绝大多数的学生在定性分析时由于定理条件不清楚,推理的逻辑欠清晰,常造成“会而不全”,导致失分. 同时学生的抽象概括能力、空间想象能力还有待提高,转化意识还有待加强.
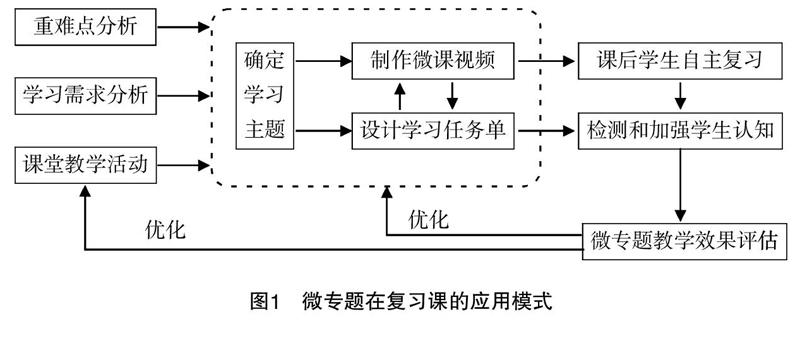
当课堂教学完成后,微专题可以作为课后复习工具应用. 学生在课堂上吸收的知识属于短时记忆,需要通过及时复习加以巩固. 微课视频可以将课堂上教师讲解过程再次回放,并可以反复播放,帮助学生复习所学知识,特别是加深对重点、难点知识的认知. 使用时应当提前做好微课视频,引导学生通过网络和移动工具开展课后补偿性学习,及时复习课堂新授知识,并引导学生抓住零散时间开展学习,进行知识的查漏补缺.
■微专题设计
1. 学习内容与学习目标分析
在点、线、面的位置关系中,直线、平面的位置关系是中心内容,其中直线、平面的平行与垂直尤为重要. 本微专题课拟通过学生在问题探索、应用过程中,对空间直线、平面的平行与垂直进行判定方法的结构性整合,进一步明确直线、平面的平行与垂直之间的内在联系. 教学重点是直线、平面平行与垂直的判定方法.
本专题采用问题——引导的模式,通过对各学习任务单问题的解决,理清空间直线、平面的平行与垂直证明之间的联系,复习巩固、熟练掌握空间直线、平面平行与垂直的判定方法,进一步明确空间直线、平面平行与垂直的相互联系. 在具体问题的探索中,整合平面平行与垂直的判定方法,从整体上掌握所学的知识并能灵活运用.
学生已具备空间直线、平面平行与垂直判定的基本知识及较为单一的判断方法,面对问题有一定的思维,能动手一试,但对直线、平面平行与垂直相互之间的联系的应用意识不强,对问题解决中知识交汇应用和综合归纳的意识不强.因此确定教学难点为直线、平面平行与垂直的判定方法的结构化整合.
根据以上分析,空间中的平行与垂直总计开发6个课时微专题,每节课提供以下内容:学习任务单、微视频(对学习任务单进行解析)、在线微检测.
2. 学习资源及学习测评的设计
微专题1:教学设计“线面平行的证明1——利用平行四边形进行转化”.
第一,明确专题指向,直击思路方法.
教师小结空间平行的证明中常见的方法.
设计意图:开门见山,进行方法归纳.
第二,精选典型例题,炼思路揭本质.
学习任务单(2016年高考全国Ⅲ卷,文科19题节选):
如图2,四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.
①证明:MN∥平面PAB;
②略.
解题思路简析:
法一(利用线线平行):取BP的中点T,可证四边形AMNT是平行四边形,进而得到MN∥平面PAB.
法二(利用面面平行):取BC的中点Q,连接MQ,NQ,可证平面MNQ∥平面PAB,进而得到MN∥平面PAB.
设计意图:以高考真题吸引学生的学习兴趣. 本题较为简单,通过本题巩固證明线面平行常见的两个转化思路.小专题微课的例题应该具有基础性、针对性、典型性和研究性. 例题的选择必须针对重点内容,巩固“双基”,贴近学生的“最近发展区”,不要过于追求难度.
第三,精选变式训练,促进技能形成.
在线微检测:如图4,在直角梯形ABCD中,AB∥CD,AB⊥AD,且AB=AD=■CD=1.现以AD为一边向梯形外作正方形ADEF,然后沿边AD将正方形ADEF翻折,使平面ADEF与平面ABCD垂直,M为ED的中点,如图5. 求证:AM∥平面BEC.
选题分析:本题的解题思路和例题相似.
设计意图:基本技能的掌握必须通过变式练习才可能内化巩固完成,练习是学生形成技能的有效途径.利用变式训练可以让学生把握问题的本质特征和解题的核心方法,加深对问题的理解,变套路为新式,从模仿到创新.
第四,自主小结方法,反思领悟提高.
学生自主小结本节课的方法,反思内化.
设计意图:反思例题、训练题,感悟出运用平行四边形转换证明平行的方法是解题的要领和注意事项,让学生的认识更明确到位.
微专题2:教学设计“线面平行的证明2——逆用平行线分线段成比例定理”.
第一,明确专题指向,直击思路方法.
第二,精选典型例题,炼思路揭本质.
学习任务单(2017年3月福州市质检节选):
如图6,在等腰梯形PDCB中,PB∥DC,PB=3,DC=1,∠DPB=45°,DA⊥PB于A. 将△PAD沿AD折起,构成如图7所示的四棱锥P-ABCD,点M在棱PB上,且PM=■MB.
①求证:PD∥平面MAC;
②略.
解题思路简析:逆用“平行线分线段成比例定理”(利用线线平行):连接BD交AC于点O,连接OM,可证得PD∥OM,进而得到PD∥平面MAC.
第三,精选变式训练,促进技能形成.
在线微检测:如图8,在四棱锥P-ABCD中,AD∥BC,且BC=2AD,AD⊥CD,PB⊥CD,点E在棱PD上,且PE=2ED.求证:PB∥平面AEC.
选题分析:本题的解题思路和例题相似.
第四,自主小结方法,反思领悟提高.
微专题3:教学设计“线面平行的证明3——利用三角形的中位线”.
第一,明确专题指向,直击思路方法.
第二,精选典型例题,炼思路揭本质.
学习任务单(2018年高考全国Ⅲ卷,文科19题节选):
如图9,矩形ABCD所在平面与半圆弧■所在平面垂直,M是■上异于C,D的点.
①略;
②在线段AM上是否存在点P,使得MC∥平面PBD?说明理由.
解题思路简析:利用三角形的中位线进行平行转化:当P为AM的中点时,MC∥平面PBD.
第三,精选变式训练,促进技能形成.
在线微检测(2016年高考四川卷,理科18题节选):
如图10,在四棱锥P-ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD=■AD,E为棱AD的中点,异面直线PA与CD所成的角为90°.
①在平面PAB内找一点M,使得直线CM∥平面PBE,并说明理由;
②略.
解题思路简析:在梯形ABCD中,AB与CD不平行. 延长AB,DC,相交于点M(M∈平面PAB),点M即为所求的一个点. (说明:延长AP至点N,使得AP=PN,可证得平面PBE∥平面DMN,则所找的点可以是直线MN上任意一点).
第四,自主小结方法,反思领悟提高.
设计说明:可以发现利用线线平行证明线面平行是其中的关键题型,而平面中证明线线平行的常用方法有:利用平行四边形的性质(微专题1),逆用“平行线分线段成比例定理”(微专题2),利用“中位线定理”(微专题3),其中微专题1和微专题3也可以先证明面面平行得到线面平行.这三个专题的难度逐渐递增,供不同情况的学生自主选择用于课后巩固,在题目的选择上,尽量选择高考题引起学生重视.
微专题4:教学设计“垂直的转化”.
第一,明确专题指向,直击思路方法.
第二,精选典型例题,炼思路揭本质.
学习任务单(2017年全国高考Ⅰ卷,文科18题):
如图12,在四棱锥P-ABCD中,AB∥CD,且∠BAP=∠CDP=90°.
①证明:平面PAB⊥平面PAD;
②若PA=PD=AB=DC,∠APD=90°,且四棱锥P-ABCD的体积为■,求该四棱锥的侧面积.
解题思路简析:①由条件得AB⊥PD,AB⊥PA,从而AB⊥平面PAD,进而得到平面PAB⊥平面PAD.
②在平面PAD内作PE⊥AD,垂足为E. 由①知,AB⊥平面⊥PAD,故AB⊥PE,可得PE⊥平面ABCD. 可得四棱锥P-ABCD的侧面积为6+2■.
第三,精选变式训练,促进技能形成.
在线微检测(2015年全国高考Ⅰ卷,文科18题):
如图14,四边形ABCD为菱形,G为AC与BD交点,BE⊥平面ABCD.
①证明:平面AEC⊥平面BED;
②若∠ABC=120°,AE⊥EC,三棱锥E-ACD的体积为■,求该三棱锥的侧面积.
解题思路简析:①先证AC⊥平面BED,再得到平面AEC⊥平面BED. ②三棱锥E-ACD的侧面积为3+2■.
第四,自主小结方法,反思领悟提高.
微专題5:教学设计“垂直的证明”.
第一,明确专题指向,直击思路方法.
第二,精选典型例题,炼思路揭本质.
学习任务单(2014年全国高考Ⅰ卷,文科19题):
如图15,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,B1C的中点为O,且AO⊥平面BB1C1C.
①证明:B1C⊥AB;
②若AC⊥AB1,∠CBB1=60°,求三棱柱ABC-A1B1C1的高.
解题思路简析:①先证B1C⊥平面ABO,再得到B1C⊥AB.②三棱柱ABC-A1B1C1的高为■.
第三,精选变式训练,促进技能形成.
在线微检测(2013年高考全国Ⅰ卷,文科19题):
如图16,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.
①证明:AB⊥A1C;
②若AB=CB=2,A1C=■,求三棱柱ABC-A1B1C1的体积.
解题思路简析:①取AB的中点O,连接OC,OA1,先证AB⊥平面OA1C,再得到AB⊥A1C. ②先证OA1⊥平面ABC,所以OA1为棱柱ABC-A1B1C1的高,又△ABC的面积S△ABC=■,所以三棱柱ABC-A1B1C1的体积V=S△ABC×OA1=3.
第四,自主小结方法,反思领悟提高.
微专题6:教学设计“垂直的综合应用”.
第一,明确专题指向,直击思路方法.
第二,精选典型例题,炼思路揭本质.
学习任务单(2016年全国卷Ⅰ,文科18题):
如图17,已知正三棱锥P-ABC的侧面是直角三角形,PA=6,顶点P在平面ABC内的正投影为点D,D在平面PAB内的正投影为点E,连接PE并延长交AB于点G.
①证明:G是AB的中点;
②在图中作出点E在平面PAC内的正投影F(说明作法及理由),并求四面体PDEF的体积.
解题思路简析:①利用线面垂直与线线垂直的相互转化以及等腰三角形“三线合一”证明. ②V=■.
第三,精选变式训练,促进技能形成.
在线微检测(2018年高考全国卷Ⅱ,文科19题):
如图19,在三棱锥P-ABC中,AB=BC=2■,PA=PB=PC=AC=4,O为AC的中点.
①证明:PO⊥平面ABC;
②若点M在棱BC上,且MC=2MB,求点C到平面POM的距离.
解题思路简析:①连接OB,先证OP⊥OB,又OP⊥AC,再推出PO⊥平面ABC.②点C到平面POM的距离为■.
第四,自主小结方法,反思领悟提高.
设计说明:本设计从学生的学习起点出发,以学生为中心,精选例题及测试题,用微型精细化原则将有关空间的平行与垂直分割成“小切口”的6个微专题,每个微专题解决一个问题,每节课充分考虑学生的认知负荷,适度适量巩固已有知识和方法.
■微专题开发
微专题开发中的微课视频制作是一个系统工作,一般从以下几个环节逐步展开:确定学习内容——撰写教学设计——制作PPT——录制微课视频——优化微课视频——开发配套资源——上传和管理微课视频. 其中微课视频制作是微专题开发的重要环节,本研究用Camtasia Studio软件录制微课视频. Camtasia Studio是一种专业视频录制和编辑软件,录制完视频可以基于时间轴进行编辑,如字幕、贴标签、画中画、媒体库、特效场景变化、画外音和主题编辑等,支持多种源文件格式及输出格式,使用方便,简单易懂. 录制微课视频时,Camtasia Studio会一起录制所选定的屏幕画面和讲授者的声音.录制视频中教师可充分利用信息技术分析题目,比如借助几何图霸动态展示变化过程.
微课视频制作完成后可发布在公共学习平台如班级QQ群或微信公眾号上,由学生课后自主学习,再收集学生的作业进行评价和反馈优化微专题资源.
■微专题教学实施建议
(1)考虑到学生的直观想象水平不一,作为课外学习的一种方法就是制作合适的微课以供学生自学巩固.通过动态的形式给学生展示图形的变化,演示各种截面、各种展开图、不同观察角度的动画. 在初学阶段可以多借助实物观察去体会,初步培养学生的空间感觉;后续阶段主要是引导学生通过解决空间位置关系的证明以及根据位置关系的转化解决一些空间角、空间距离、空间最值等问题. 在大量的自身体验之后获得经验,从而发展直观想象素养. 针对比较复杂的综合性问题,可采取分层次的方式逐一突破,化整为零;也可细分为某一些微专题,再整合成一个整体. 因此教师可以利用微专题为学生铺设台阶逐步提升直观想象素养.
(2)加强现代教育技术与学科教学的融合. 利用信息技术多媒体辅助教学,比如几何画板、几何图霸、希沃白板等多媒体技术演示动图让学生体会空间关系. “动则悦,静则思”. 在立体几何教学中可以让学生在三维动态中沉浸体验,在直观图注视上宁静思考.比如空间几何体的不同视角的动态展示,三视图与直观图的转换过程,以及平面图形的翻折与展开问题,借助信息技术动态演示,能便捷直观地了解图形的特点.
(3)微课的优点是主题突出、时长较短,便于学生利用零碎时间针对自身的疑难问题进行自主学习,能够更好地满足学生的不同学习需求,作为课堂的延续可以给课堂教学扩容,提高学生的自学能力,实现效益最大化. 微课不同于文本,能从视听角度给学生不一样的刺激,可视,共享,储存方便,借助网络突破时间、空间的局限,学生可以更自由地把握学习时间,对重点、难点的问题可以反复观看,也可以自主选择薄弱知识或题型总结的微课反复观看.
总之,应合理设置微专题帮助学生突破学习难点并巩固重点. 积极有效地将微课的直观和微专题的短平快、高效简洁的特点结合起来,发挥二者“因微而准、因微而细、因微而深”等优势.

