全机静力试验预警方法的研究

柴东波，郭晓冬，杨东涛

(中国飞机强度研究所，陕西 西安 710065)

1 引 言

全机静力试验作为飞机研发过程中的设计、制造、试验、试飞等4大环节中不可或缺的第3棒[1]，是保障型号安全首飞和持续试飞的先决条件，其目的是鉴定飞机结构设计的静强度，并为验证强度和刚度的计算方法和结构设计、制造工艺的合理性提供必要的数据和资料[2]。应变数据作为全机静力试验中一项重要的测量结果，能够直观地反映试验件在试验过程中的受载情况。因此，对应变数据的实时监控和快速分析，对保证试验的顺利进行有着至关重要的作用。

民机尽早投入商业运营是提升我国民机国际竞争力的关键因素，高效的全机结构试验是提高民机型号研制效率的重要保障。目前，国内飞机研制过程中，由于前期部件静力试验的验证不够充分，这使得全机静力试验中布置的应变计多达上万片，尤其是在大飞机的研制过程中，应变计最多可达30000余片。在试验过程中，有限的人力资源只能监控其中少量的重要部位应变变化，这就给试验的顺利进行带来了一定的风险。因此，需要一种在试验过程中能够及时发现试验数据异常变化的方法，试验人员可据此及时做出判断，以保障试验的顺利进行。

飞机在限制载荷试验期间，结构不得发生有害变形；在极限载荷试验期间，结构至少应承受3s极限载荷而不发生破坏[3]。一般飞机在限制载荷静力试验期间，其变形应当在材料的线弹性阶段，即应变数据随载荷的线性增加呈线性变化。在极限载荷试验期间，飞机变形超过材料屈服极限的部位或结构发生失稳将是试验人员重点监控的部位。因此，试验数据随试验载荷是否线性变化是判断试验数据是否异常的重要判据。

目前，国内对静力试验过程中预警方法研究较少，主要通过多人分部位监控试验数据。韩凯[4]等对试验过程中的异常试验数据进行了分类和研究，但主要针对的是失效试验数据产生的原因；侯乔乔[5]则对应变数据典型形态进行了分析；王霞光[6]等提出了基于线性相关系数的方法判断数据的线性，但此种方法对异常试验数据的判断不够敏感。

本文利用线性回归方程，计算标准差，基于拉依达准则定义偏离度，对偏离度超过e(即2.72)的试验数据认为是异常试验数据，在试验过程中应当予以重点关注。

2 判断准则

2.1 线性回归方程

判断试验数据是否线性变化，首先需要确定试验数据的线性回归方程。

y=ax+b

(1)

其中：

2.2 样本标准差

试验数据的标准差可以反映试验数据的离散程度。标准差越大，表示试验数据的离散度越大，重复性越差；相反，标准差越小，表示试验数据的离散度越小，重复性越好。

测量值与线性回归方程计算值的标准差，可以反映试验数据的线性变化。利用贝塞尔公式计算样本标准差：

(2)

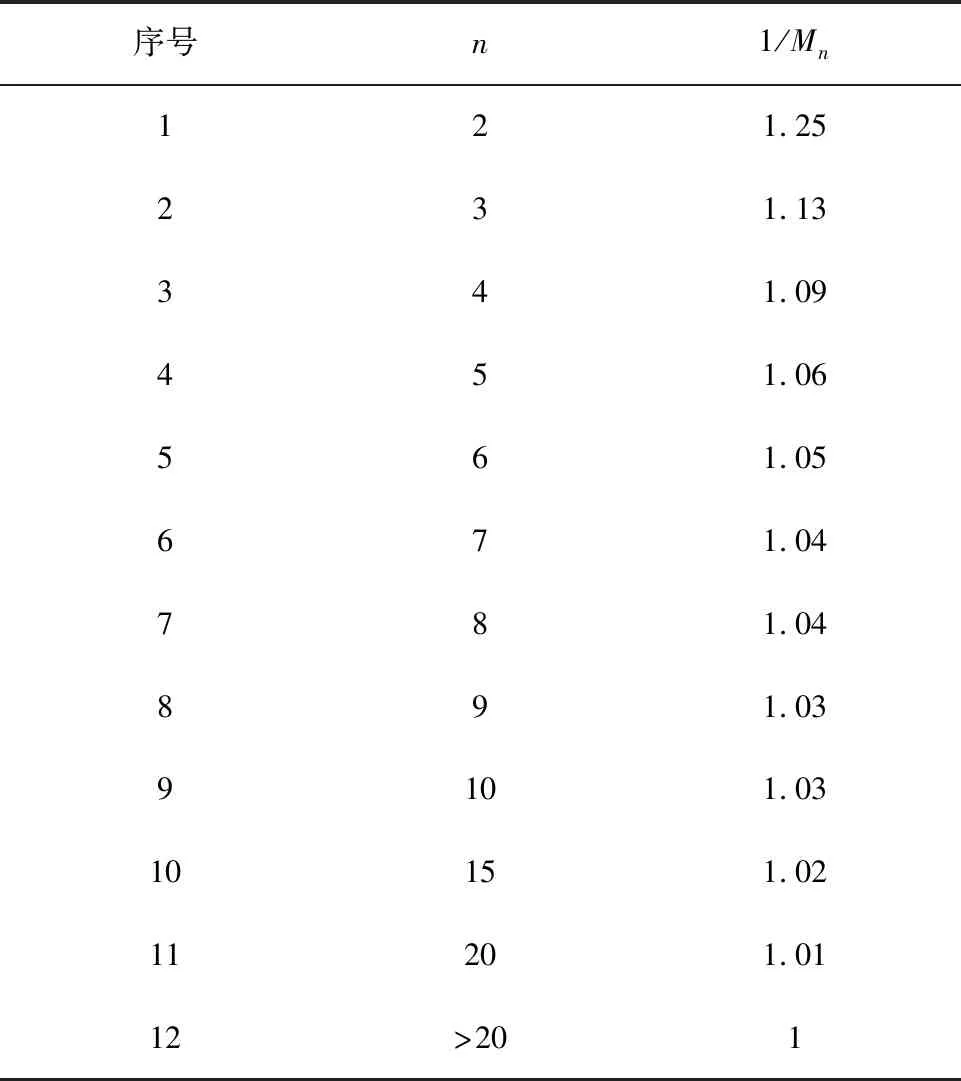
表1 贝塞尔公式修正因子

2.3 偏离度

采用拉依达准则(3σ-rule)，通过统计一组试验数据与其线性回归方程计算值的差来判断该数据是否为异常数据点，具体公式如下：

(3)

基于试验数据的线性回归方程计算值、标准差及拉依达准则构建试验数据的偏离度d：

(4)

偏离度为测量点偏移线性回归方程计算值的程度[7]。试验数据呈线性变化时，试验数据的偏离度很小，d接近于1；试验数据在正常情况下，d值不超过e(即2.72)；试验数据的偏差在超过3σ后，d急剧变大。因此，试验测量值的偏离度在超过e(即2.72)之后，可以认为试验数据呈非线性变化，应当进行重点监控，分析出现此种现象的原因，并预测试验数据的变化趋势，判断继续进行试验的风险。

3 试验数据处理的一般步骤

现在飞机的全机静力试验，在正式试验前，一般会进行60%限制载荷的静力试验，用于验证加载设备、控制系统和测量系统的工作状态，并通过试验数据对整体试验进行初步的分析确认。因此，可以利用60%限制载荷静力试验的试验数据确定每个测量点的线性回归方程和标准差。在正式试验中，利用各测量点的线性回归方程与标准差计算偏离度，监控各测量点每级数据是否呈线性增长，实现对试验数据的实时监控预警。

3.1 剔除无效数据

一般情况下，试验数据会受一些因试验件内部应变计损坏、环境干扰信号等不可避免的因素产生的影响，通常称为无效数据，其不能真实地反映试验件对所施加载荷的响应，因此在试验数据处理与分析之前予以剔除。全机静力试验无效数据的判断依据[6,8]为：

(1)测量结果超大(超出材料极限强度的应变值、超出采集系统允许的最大量程)；

(2)测量结果跳跃(呈大范围无规律的异常跳动现象)；

(3)测量结果为纯零。

3.2 确定线性回归方程

现在飞机设计要求，结构必须能够承受限制载荷而无有害的永久变形，即在60%限制载荷静力试验中，试验件的变形应在材料的线弹性阶段。因此，试验数据在此试验阶段理论上呈线性变化。

对于60%限制载荷静力试验，载荷以5%限制载荷为一级，逐级加载至60%限制载荷。由于受到加载设备自身重量的影响，各级载荷在加载初期往往是非线性增长。因此，在确定线性回归方程时，必须考虑加载设备扣重完成的载荷级数。根据试验的经验，加载设备扣重完成的载荷级数一般不会超过20%。因此，可以利用20%～60%限制载荷区间内的试验数据在剔除无效数据后，确定各测量点的线性回归方程。

3.3 确定标准差

在全机静力试验中，加载点的数量往往有上百个，每个加载点根据加载载荷的不同，选用的加载作动筒大小和力传感器的量程也不同。不同的加载点，控制误差也各不相同。但在每次试验中，每个加载点的误差控制自始至终是固定的。因此，在60%限制载荷静力试验中，计算得到的各测量点标准差可以作为正式试验的标准差。

3.4 试验监控

在正式的全机静力试验中，将测量点编号、线性回归方程(系数a、b)和标准差导入监控软件。监控软件得到试验数据时，根据试验数据的载荷级数，利用线性回归方程计算所对应的期望值。通过测量值、期望值、标准差，利用式(4)求出偏离度d。如果偏离度d超过e(即2.72)，则对此测量点进行预警，进行重点监控，分析出现该现象的原因和其下一步的数据变化趋势。

4 案例验证

以某型飞机全机2.5g极限载荷静力试验812305号测量点(位于右机翼下壁板)为例，验证该预警方法的实际应用情况。2.5g全机稳定俯仰静力试验是飞机全机静力试验中机翼受载最严苛的工况，也是业内公认的高难度、高风险的试验工况[9]。重点考核部位为机翼盒段、中央翼盒段及中机身。试验采用胶布带杠杆系统加载、双层地板梁加载、假件接头加载等加载方式。60%限制载荷试验测量数据如图1所示。

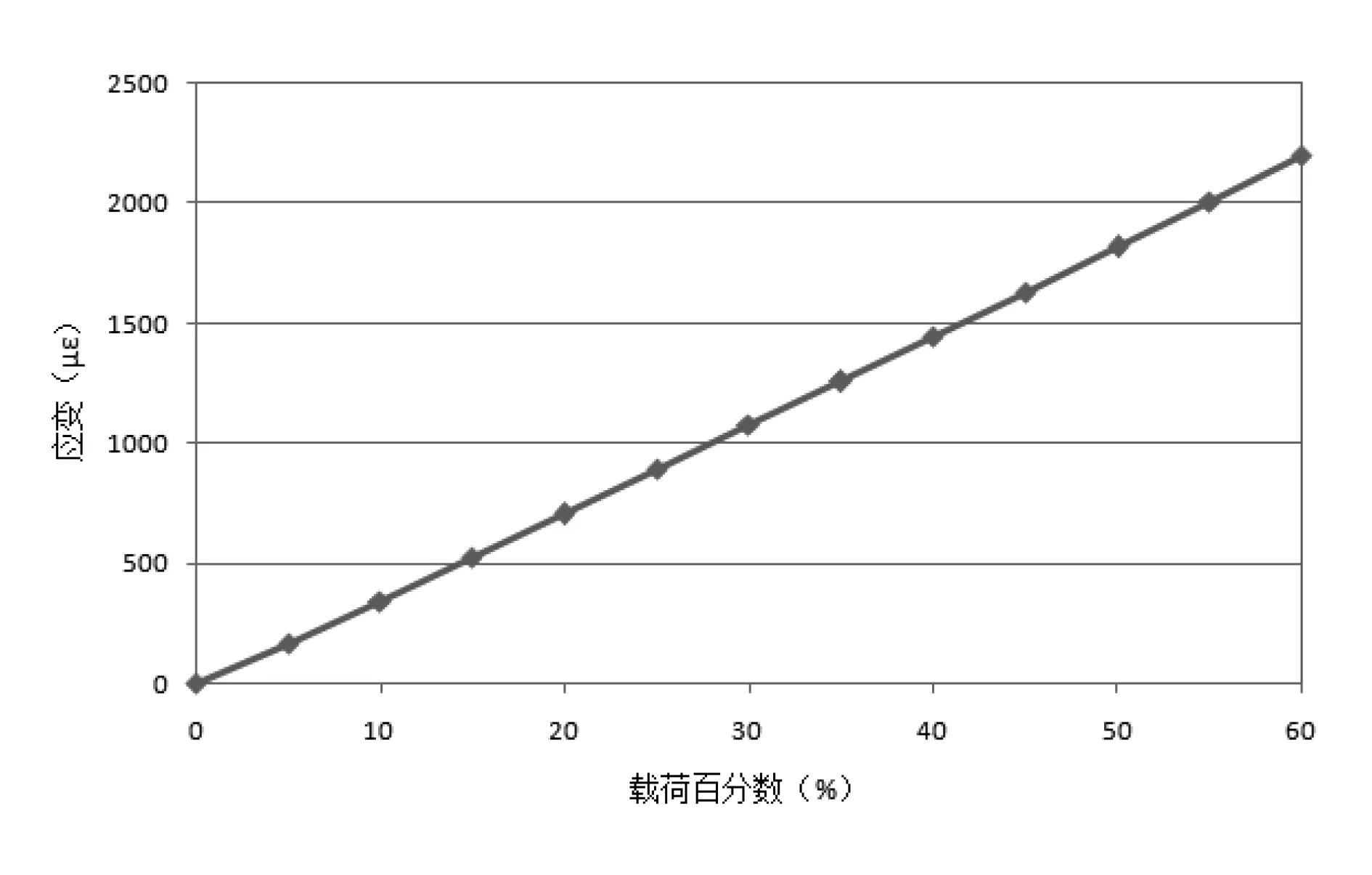
图1 60%限制载荷试验载荷应变曲线图

根据本文提出的预警方法，利用20%～60%限制载荷区间确定线性回归方程为：

y=37.28x-42.96

将上式代入式(2)中，求得20%～60%限制载荷区间的标准差σ为15.32。

利用线性回归方程y=37.28x-42.96和标准差σ=15.32监控150%限制载荷试验，测量数据如图2所示，偏离度如表2所示。

图2 150%限制载荷试验载荷应变曲线图

通过图2、表2可以看出，在20%～105%限制载荷区间内试验数据呈线性变化，各级试验数据的偏离度在1～2.72之间变化。110%限制载荷后，试验数据呈非线性变化，并且随着试验载荷的增大，试验数据的偏离度急剧增大。

5 结 论

本文以全机静力试验60%限制载荷试验的试验数据为标准样本，构建线性回归方程并计算相应的标准差，基于线性回归方程和标准差构建偏离度。在正式试验中监控偏离度的变化，可以快速识别非线性变化的试验数据，并进行预警，方便试验人员重点监控和进一步分析试验数据的变化趋势，分析试验数据出现非线性变化的原因，这对降低全机静力试验的风险具有重要的意义。