扭矩扳手检定装置受力杆结构优化分析

田成成

(滨州市计量测试检定所，山东 滨州 256606)

1 引 言

扭矩扳手检定装置是一种用于对扭矩扳手进行力值检定的试验装置。在力值检定过程中，受力杆在扭矩扳手反作用力的作用下会产生一定的弹性形变，影响检定数值的准确性。在以往的设计中，通过增加受力杆的尺寸来减小检定过程中受力杆的变形对检定数值造成的影响。这种设计理念使得检定装置相对笨重，影响了使用过程中的灵活性，也在无形中增加了制造成本[1]。

利用ANSYS Workbench建立仿真模型对受力杆进行静力学分析，模拟其在对扭矩扳手进行力值检定时在扭矩扳手反作用力下的应力、应变及变形情况，并根据测得的数据对其进行了结构优化设计、轻量化设计[2]。

2 受力杆结构

受力杆总长1045mm，厚24mm，材料为45号钢，其抗拉强度600MPa，屈服强度355MPa，质量为10.677kg[3]。受力杆由一端钻有圆孔的长方体实体和圆环组成，如图1所示。受力杆的圆环与标准扭矩传感器连接，圆孔处与滑动支撑连接，受力杆的长方体实体侧面承受局部压力。

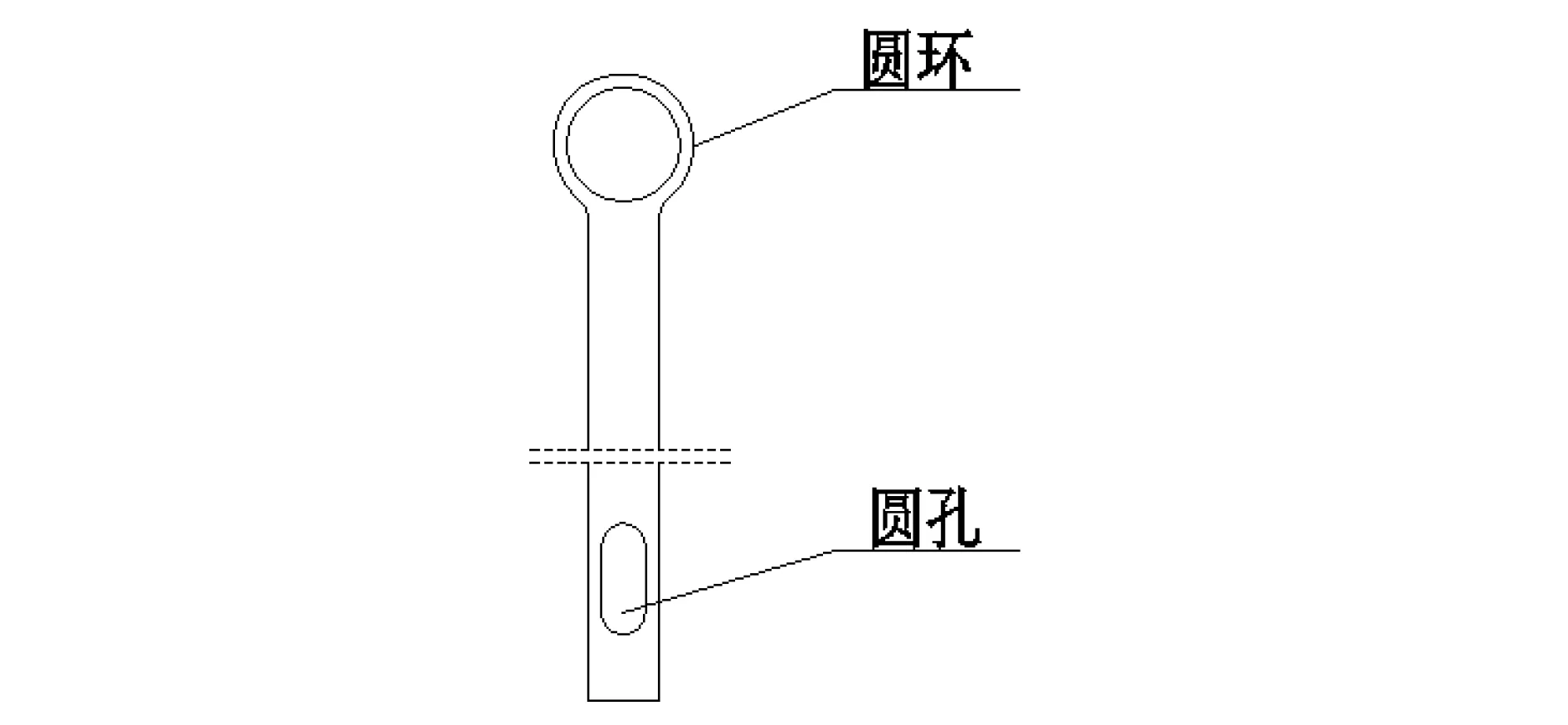
图1 受力杆结构

3 受力杆的静力学分析

扭矩扳手检定装置设计所能检定的最大扭矩为1000N·m，其扭矩方程为：

M0=F·L

(1)

由于最大扭矩M0=1000N·m，力臂L=714mm，则受力杆侧面承受局部压力F=1400N。

建立受力杆的有限元分析模型，定义材料属性：弹性模量为2.09×105MPa，泊松比为0.269，密度7.89×103kg/m3。其结构动力学方程[4]：

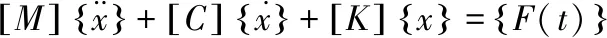
(2)

式中，[M]为质量矩阵；{x}为位移矢量；[C]为阻尼矩阵；[K]为刚度系数矩阵；{F}为力矢量。

受力杆结构为连续体，且结构在载荷下的应力、应变及位移也是连续的，结构材料变形满足虎克定律，受力杆线性静力分析不受时间因素的影响，速度、加速度变量可以约掉[5]，方程变为：

[K]{x}={F}

(3)

根据受力杆整体尺寸及结构特点设置合适的网格尺寸精度，对受力杆进行自动网格划分。网格划分后的模型节点数为753915，网格数为171264。对完成网格划分的受力杆模型的圆环和圆孔处施加固定约束，在受力杆侧面力臂L=714mm处施加局部压力F=1400N。求解完成后，查看受力杆在载荷F作用下的等效应力、总变形和Z轴变形云图[6]，如图2-图4所示。

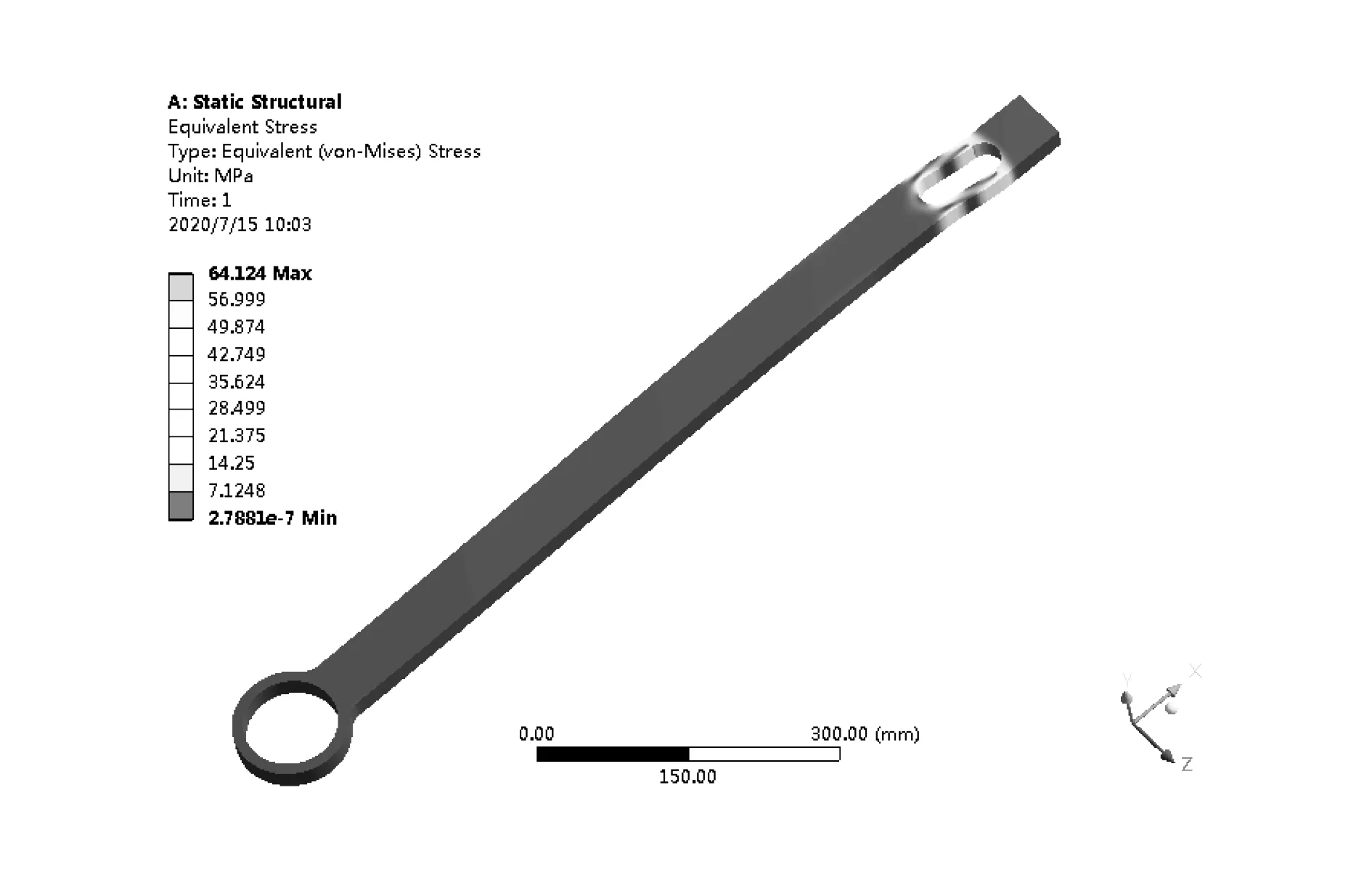
图2 受力杆的等效应力云图

图3 受力杆的位移总变形云图

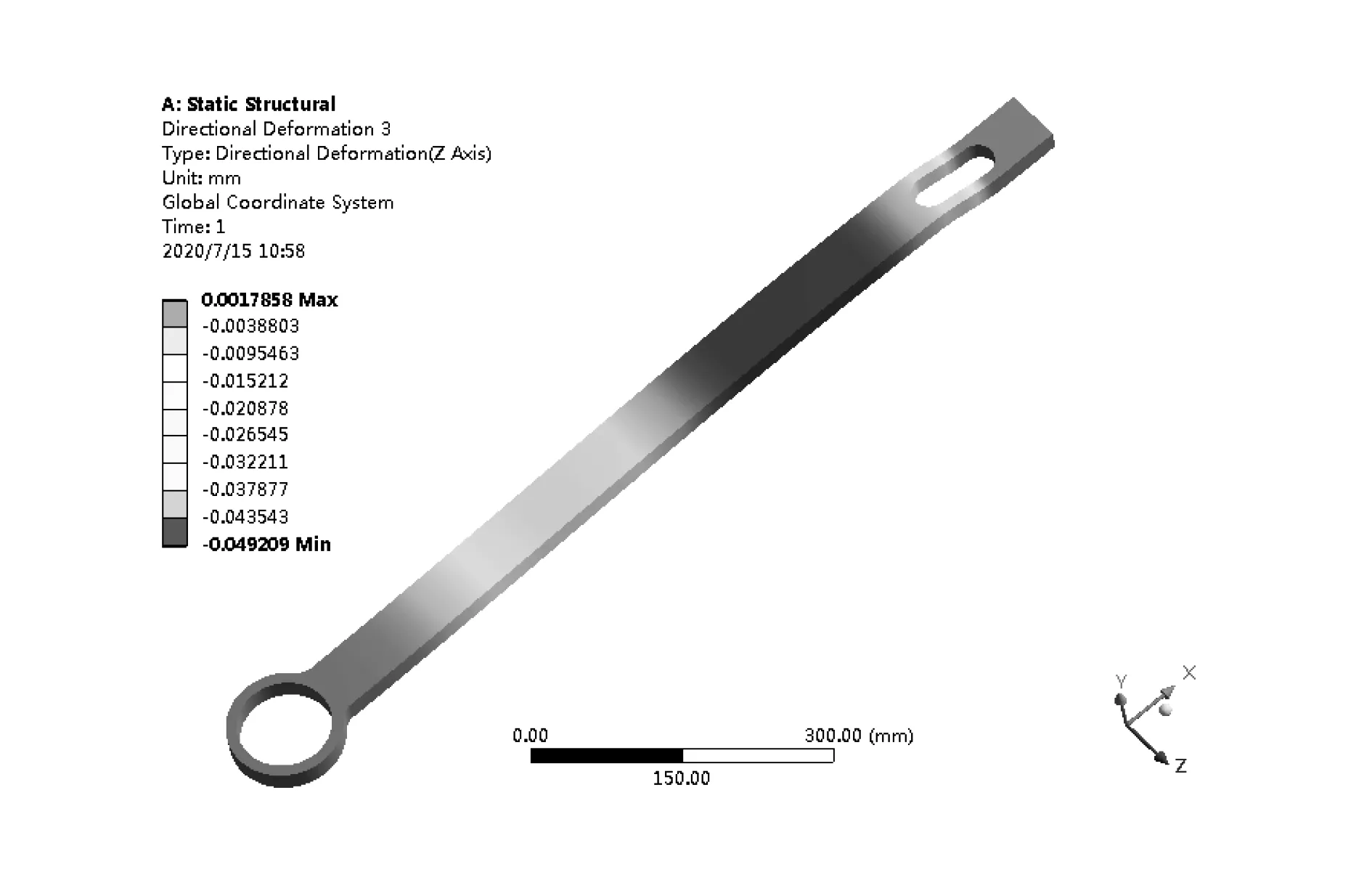
图4 受力杆的Z轴位移变形云图

从图2、图3、图4可以看出，受力杆的最大等效应力σmax=64.124MPa，最小应力σmin=7.1248MPa；最大位移总变形δmax=0.049mm，Z轴最大位移变形δzmax=0.049mm。受力杆的最大等效应力出现在应力集中的轴孔处，其最大值远小于材料的强度。受力杆Z轴方向位移变形与受力杆位移总变形的一致性表明，受力杆在侧面局部压力F的作用下产生Z轴方向的弹性变形，且最大变形量0.049mm远小于扭矩扳手在检定过程中的变形，其对检定过程中数值的影响可以忽略不计[7]。

4 受力杆的结构优化

通过对受力杆的静力学分析可以得出，受力杆的最大等效应力远小于材料的许用应力，受力杆的位移变形量也很小，可对该结构进行优化处理。由于受力杆的中间部位承受应力较小，可以采用工字形结构代替长方体实体的实心结构[8]。受力杆优化后的结构图如图5所示。

图5 优化后的受力杆结构

对优化后的结构进行相同载荷和约束下的静力学分析，结构优化后的等效应力云图、位移总变形云图如图6、图7所示。受力杆结构优化前后的质量、最大位移总变形量、最大等效应力对比如表1所示。

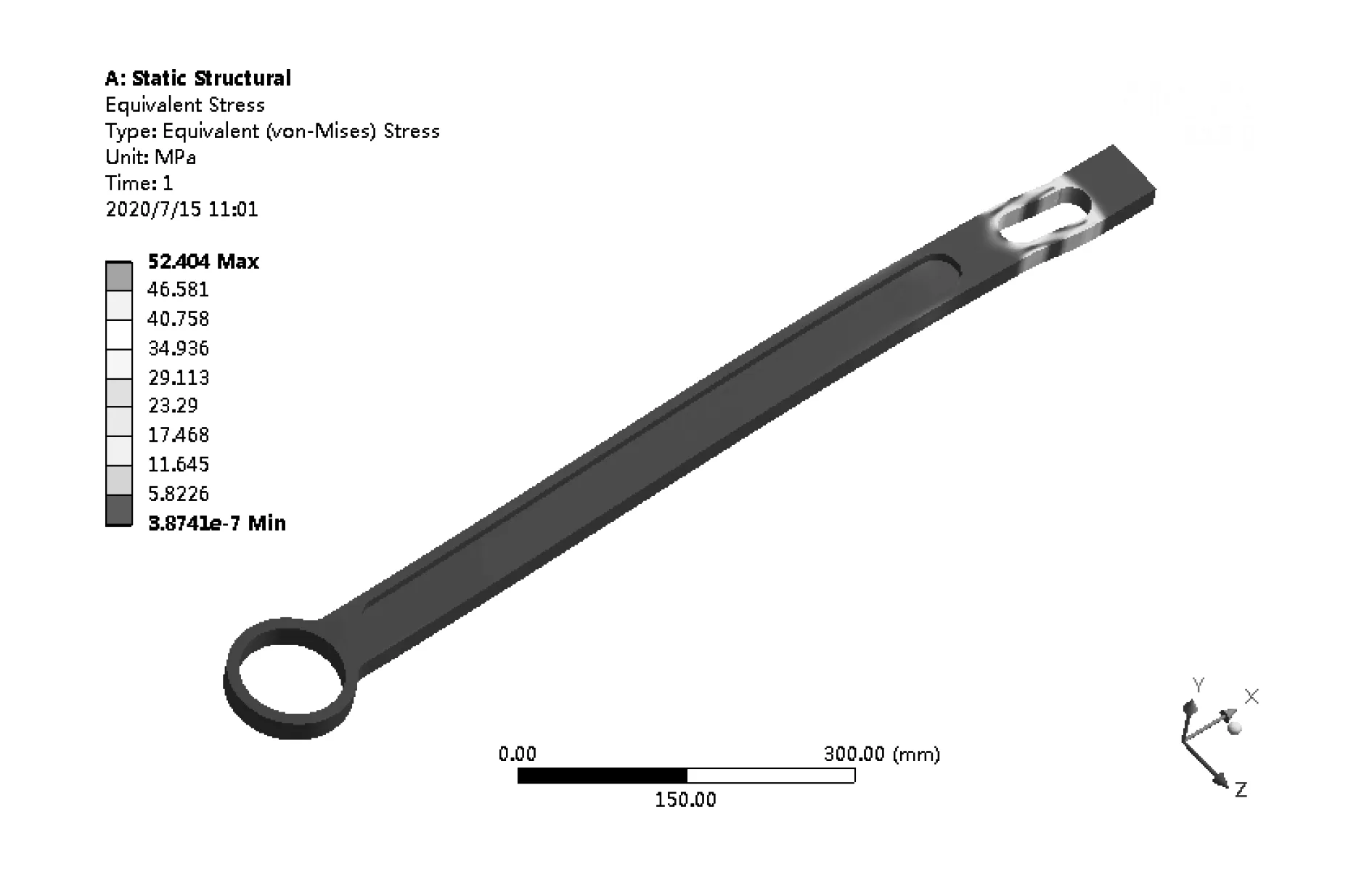
图6 受力杆优化后的等效应力云图

图7 受力杆优化后的位移总变形云图

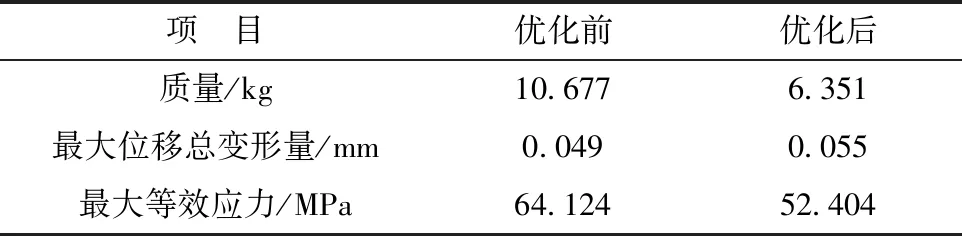
表1 受力杆优化前后对比

通过受力杆优化前后对比可知，受力杆的质量减小40.5%，最大等效应力减小15.6%，其原因为采用工字形结构减小了中间支撑的刚性，对圆孔处的应力集中起到的了一定的缓和作用。最大位移总变形量增加了0.006mm，可以忽略。优化后的最大位移变形量和最大等效应力都在许用范围之内。从对受力杆的优化结果分析中可以看出，采用工字形结构的优化方案可以在满足结构强度和变形量的前提下，实现结构的轻量化设计。

5 结 语

通过对扭矩扳手检定装置受力杆结构的分析与优化可以看出，优化后的受力杆质量减小40.5%，并且可保证最大等效应力和最大位移变形都控制在许用范围内，达到了节约材料、减轻质量的目的，为今后相关产品的设计提供了改进的方向。