散乱数据拟合的自适应分片逆尺度空间算法

钟轶君， 李崇君

(1. 浙江理工大学理学院数学科学系，浙江 杭州 310018；2. 大连理工大学数学与科学学院，辽宁 大连 116024)

散乱数据拟合(函数拟合/逼近)是一个在信号处理、计算机图形学中被广泛研究的问题。其通过给定的散乱的、带噪音的点集来拟合一个较好的曲线或曲面，需要解决2个基本问题：①如何选择一个简单的函数空间作为描述对象函数的逼近空间；②其空间要有很好的逼近度。为此，随着散乱点曲面拟合工具多样性的不断探索，有学者开始利用探索多层结构性质来改进逼近方法，如LEE等[1]提出的基于B样条的多层逼近方法；CASTANO等[2]提出了基于小波的多层正则化方法等。JOHNSON等[3]进一步探讨了在平移不变空间(principal shift invariant，PSI)中基于 B样条和小波的散乱点曲面拟合问题。以上方法均力求在所构建的函数类中与研究对象函数本身误差最小。对于第②个问题，学者们希望在其空间中得到散乱数据的稀疏表示解，因此推动了稀疏逼近和优化方法在函数拟合领域的广泛应用。随着深层挖掘曲面中的稀疏性，几何建模中很多的启发式方法得到了进一步发展和推广。近些年，信号的稀疏性研究也取得了丰硕的成果，其中细化研究信号的稀疏分布(非零元素的分布)成为了热点，如HUANG[4]提出了结构化稀疏的概念，即一类非零元具有一定结构性的稀疏向量，如广泛研究的非零元是成块出现的块稀疏[5-9]，在统计中也称为Group Lasso[10-17]，除此之外还有树稀疏[18]、图稀疏[19]。刘翼鹏[19]讨论了向量服从全局稀疏、局部分布不同的凸优化模型，讨论了全局稀疏局部稠密，即非零元素呈簇状分布的稀疏向量。提取出了可以描述整个信号的结构性信息，有利于使用更少的样本和运算量来恢复信号，且能够决定信号是否可以有效地得到恢复。对于不同的实际场景，信号的稀疏表示向量具有不同的结构，更好地研究这些结构有利于理解和解决实际问题。随着对稀疏性的细化探索，学者们尝试在曲面重构，尤其是在PSI空间中的曲面重构问题所具有的结构型稀疏表示进行研究。HAO 等[20]提出了利用凸优化模型来考虑PSI空间中基于B样条的散乱点曲面拟合问题，利用多块LASSO (MLASSO)得到散乱点曲面拟合问题的稀疏解；文献[21]得到了曲面在PSI空间中每一层 B样条上的稀疏表示解。基于MLASSO的散乱点曲面拟合问题不仅可以得到稀疏解(稀疏表示系数)而且拟合效果较好，但其多个正则化参数的选取是一个待解决的问题。OSHER等[22]提出 Bregman逆尺度空间算法(inverse scale space，ISS)，即

此方法是贪婪算法和凸优化算法的一种结合，不仅规避了凸优化算法中参数的选取问题而且运行速率较快。之后LI和ZHONG[23]提出了一种带有删除机制的分片逆尺度空间算法，核心是将分片稀疏性引入到ISS算法中。在稀疏恢复问题上，相较于ISS算法，该算法能够更好地保护信号的小尺度非零元素，在应用于散乱数据拟合问题中得到了较好的拟合效果。分片稀疏性是一类描述向量中非零元素散乱分布现象的稀疏性。DONOHO和HUO[24]针对片稀疏信号对应观测矩阵具有的分块结构，引入分块矩阵互相干(mutual coherence)条件，可将分块正交矩阵的精确恢复信号的稀疏度理论上界推广到一般分块矩阵之中, 改进了稀疏信号可精确恢复的充分性条件。其结果不仅给出了分片稀疏恢复的理论保证，也提升了L0模型和压缩感知恢复整体稀疏信号的可信度。向量的分片稀疏结构所对应的观测矩阵A的分块结构恰好符合PSI空间基于 B样条所生成基函数的层数，因此引入分片稀疏性到稀疏优化算法(模型)中，并分析散乱点曲面拟合问题是有意义的。

然而分片ISS算法(P_ISS)[23]也有其缺陷，算法中的删除机制增加了新的参数选取问题。目前考虑基于散乱点的曲面拟合的稀疏表示的文献较少。基于此，本文提出一种自适应的分片逆尺度空间算法(adaptive piecewise ISS，aP_ISS)，由此得到散乱点曲面拟合问题的稀疏表示。此算法不仅规避了带有删除机制的分片逆尺度算法中需要人工选取参数的问题，而且通过对“分片符号一致性”的分析，使得算法具有自适应性，可更好地应用到散乱点曲面逼近问题中。

本文主要贡献如下：

(1) 通过将分片稀疏的理念引入到散乱数据拟合问题中，拓广了稀疏技术在函数逼近中的应用。

(2) 改进了文献[22]中的分片逆尺度空间算法，规避了算法中的删除机制。利用“分片符号一致性”使得算法更具自适应性。

(3) 稀疏算法作为高效算法已经成功地应用到了曲面拟合问题中，本文建立了一个稀疏表示系数的先验信息，从而可以更好拟合曲面的细节信息，达到更好地逼近效果。与已有的稀疏重建算法相比，不仅有更松弛的理论保证并且拟合效果更好。

1 预备知识

1.1 散乱数据曲面拟合问题

典型的散乱点曲面拟合问题是指：存在一个散乱点集合X={x,x,… ,x} ⊂Ω⊂Rd和相对应的函数值f|X= {f1,f2, …,fn}，且需要找到一个属于空间H的函数g能够拟合给定的数据 { (xk,fk) }nk=1。经典的光滑样条散乱点重构模型为

由于g属于Beppo-Levi空间，所以当数据点规模变大时计算量也会变大。为了解决该问题，文献[3]考虑在一个由紧致支撑函数移位扩张生成的空间(称为 PSI空间)中求解以上正则化问题。利用PSI空间不仅避免了计算量增大的问题，也由于其和小波、B样条的联系使得稀疏逼近数据函数成为可能。

利用分块矩阵A= [A1, … ,AN]表示由定义的观测矩阵

向量bσ表示被噪音污染的数据{fi}，则曲面拟合问题g(xi) ≈fi可以记为bσ=Ax+e，其中x为曲面表示系数；e为噪音。

1.2 符号说明

定义1[24].观测矩阵A的列互相干为

其中，ai为矩阵A的第i列。

定义 2[23].设矩阵A= [A1, … ,AN]是N个矩阵的拼接，定义第i块的子阵互相干为

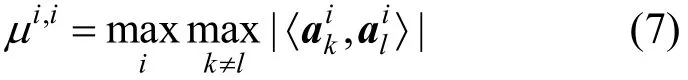
命题1[23].第i块的子阵互相干μi,i满足

其中，αi∈[0,1]为衡量第i个子矩阵块内互相干与矩阵整体互相干比例关系的参数。

Oracle估计[21]是最小二乘解在真实支撑集S上的部分，oracle的非零元素可表达为

分片oracle估计[22]是oracle估计限制在子空间Si上的部分

1.3 逆尺度空间算法

文献[25]中提出了一个自适应的逆尺度空间算法(adaptive inverse scale space，aISS)，实现算法步骤如下：

输入：A，bσ,threshold ≥ 0 。

输出：x(tk)。

步骤1.初始化

步骤2. 计算x(tk)为问题

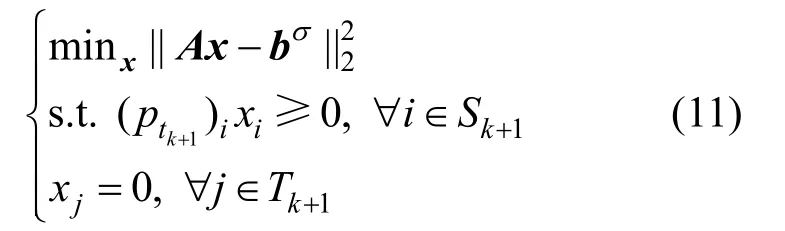
在Sk=Ik上的解。

步骤3.更新时间变量为

步骤4.更新次梯度为

其中，t=tk+1，ejn∈R为第j个分量为1其余分量为0的向量。

步骤5.更新指标集为

文献[21]中给出了如下ISS系统(1)的理论保证条件。

假设 1[21].限制强凸性(restricted strong convexity)：存在γ∈ ( 0,1]，使得

假设 2[21].不可表示条件或精确恢复条件(irre-presentable condition or exact recovery condition)：存 在η∈ ( 0,1)， 使 得其中

定理1[21]. 设假设1和2均成立，那么存在一个时刻τ使得Bregman ISS路径(1)在时刻τ之前没有错误选择，即∀t≤τ，supp(x(t)) ⊆ supp(x)以大于的概率成立。若

的概率有sign(x(τ))=sign(x)，即Bregman ISS求解的最优解达到了符号一致性。

1.4 分片稀疏

对于给定的向量

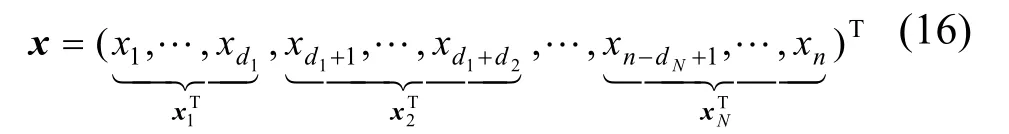
(1) 全局稀疏。x称为s-稀疏的若x至多含有个非零元素；

(2) 块稀疏[4-9]。x称为块s-稀疏的若x至多含有s个含有非零元素的块，即块l0范数2,0||x||=不超过s；

(3) 分片稀疏[23]。向量可以分成N个部分，且每部分xiT∈Rni都是一个稀疏向量，若已知si=||xi||0(i=1,…,N)，则称x是分片(s1,… ,sN)-稀疏向量。

1.5 分片逆尺度空间算法(P_ISS)

分片逆尺度空间系统(piecewise inverse scale space，P_ISS)[22]旨在恢复分片稀疏向量中每一个子向量∈Rni的支集，即P_ISS方法分别且同时求解xi，再由所有的xi共同构成x，即

算法1[22].分片逆尺度空间算法

输入：观测矩阵A= [A1, … ,AN]，观测向量bσ，噪音程度参数σ。

输出：分片稀疏向量x=(x1T, … ,xTN)T∈Rn。

步骤1.初始化。

步骤2.最小二乘。更新为

的解。其中I为指标集；IP为在指标集I上的投影算子。

步骤3.并行时间路径更新。

步骤4.并行的次梯度向量更新。

步骤5.并行的指标集更新。

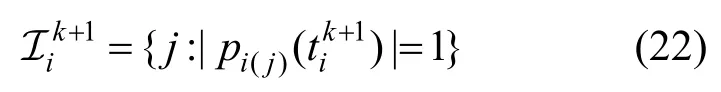
步骤6.删除机制。设置向量

满足不等式

的分量为0。引入分片稀疏性后提出的带删除机制的分片Bregman逆尺度空间(P_ISS)算法。因该算法结构类似于正交匹配算法，所以其运行速率较快，又因求解的是分片凸优化问题，故其收敛到l1稀疏解。数值实验表明相比于 ISS算法，分片Bregman逆尺度空间算法能够更好地保护小尺度元素不被噪音混淆。

2 自适应分片逆尺度空间算法(aP_ISS)

2.1 P_ISS算法中删除机制的缺陷

在改良的贪婪算法中，比如压缩采样匹配追踪算法 (compressive sampling MP，CoSaMP)[26]，利用删除机制对算法当前恢复的解进行自适应的修正是较为常用且有效的方法。CoSaMP在算法最后一步保留最大的s(s=||x||0)个非零元素，其余的元素均设置为0以克服类似StOMP算法[27]在支集添加冗余元素的缺陷。在算法P_ISS迭代过程中，由于分片稀疏向量x整体到达符号一致性[22]的时刻其中iτ为第i片到达符号一致性的时刻。即所有的“片”到达了符号一致性算法才会停止更新支集。在所有的N个子向量都到达符号一致性之前，早到达符号一致性的“片”会由于不断的迭代产生错误或冗余的非零元素，所以在P_ISS算法中设置删除机制可以有效地避免冗余元素的产生。但是，删除机制中引入的参数C使得算法增加了选取问题，即参数C与数据密切相关，需要经验性选取，消耗大量时间。

2.2 分片符号一致性

本文考虑对算法进行分片符号一致性的改进，即当某一“片”到达符号一致性时, 停止此“片”的支集更新。从而保证在最小二乘计算中，该“片”不会随着晚到达符号一致性的“片”的更新而增加冗余的元素。该算法自行地对每一“片”实行分片符号一致性的“监督”，使得算法自适应性更强。

2.3 自适应分片逆尺度空间算法(aP_ISS)

算法2.自适应分片逆尺度空间算法

输入：观测矩阵A= [A1, … ,AN],观测向量bσ，噪音程度参数σ。

输出：

步骤1.初始化。

步骤2.最小二乘。更新为

的解。其中，I为指标集；PI为在指标集I上的投影算子。

步骤3.并行时间路径更新。

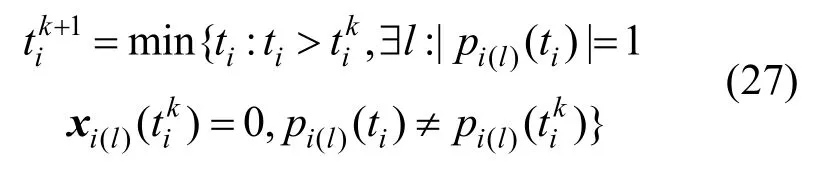
步骤4.并行的次梯度向量更新。

步骤5.并行的自适应的指标集更新。若第i片未达到符号一致性，则

实际算法操作中，通过算法当前迭代向量和oracle向量的符号一致性，即考虑第i片的向量xi和分片oracle估计向量是否达到了符号一致性

并衡量是否更新指标集。下面给出 aP_ISS的性能保证定理。首先给出一些相关的引理。

引理1.矩阵AS= [AS1,…,ASN]的奇异值Λ满足

其中，

证明：在每个子矩阵Ai中，选择指标集为Si的列向量组成的子矩阵ASi。考虑Grassmannian矩阵

其中，Φij为ΦS中的元素，且ΦS中对角线元素满足非对角线元素满足|Φij| ≤μ。因此

证毕

引理 2.设矩阵A= [A1, … ,AN]的每一个子矩阵Ai的互相干参数是αi，假设1成立，则

其中，

定理2.设假设条件1和2均成立，若分片稀疏信号满足

其中，smax为si=|Si|的最大值；

3 数值实验

3.1 实验设计

本文的散乱数据曲面拟合问题，对应于分片稀疏模型，矩阵A= [A1, … ,AN]是由定义的观测矩阵带噪音的观测数据{fi}是用向量bσ表示。此部分通过给定的散乱点集{xk,yk}和其相对应的观测数据{f(xk,yk)}拟合曲面并得到其稀疏表示g(x,y)。其逼近函数是由张量积 B样条基函数(x,y)(i= 1 ,…,N;j= 1,…,ni)表示，其中N为多层B样条的层数，基函数的总数为n=n1+…+nN，于是待拟合曲面为

考虑到N层B样条基函数之间是相关的，于是此问题转变为了一个求解分片稀疏向量(曲面的系数向量)，即

的分片稀疏逼近问题。

本文通过对一个函数f添加高斯噪音来人工生成一个带噪音的数据集{((xk,yk) ,f(xk,yk)):k=1,… ,9 00}，即

对比以下算法求解散乱数据曲面拟合问题的稀疏表示的数值效果：

(1) 逆尺度空间算法(aISS)。

(2) 带有删除机制的分片逆尺度空间算法(P_ISS)，其中删除机制中参数C=0.3。

(3) 多块LASSO (MLASSO)利用Jacobi型的逼近交替方向乘子算法(alternating direction method of multipilers，ADMM)[28]求解MLASSO，其中正则化参数的值取为γ1=0.3，γ2= 0 .15，γ3=0.2，γ4=0.3。

(4) 本文提出的自适应分片逆尺度空间算法(aP_ISS)。通过均方根误差(root-mean-square，RMS)、分片稀疏度及算法运行时间(CPU)进行4种算法比较，RMS为

其中，

3个噪音分别取值为σ1= 0 .25,σ2= 0 .1,σ3= 0 .01。

3.2 实验结果分析

从表1～3的数值结果和图1～3的拟合效果可以发现，若不考虑分片稀疏性的a_ISS算法，本文算法(aP_ISS)较其他 2种算法在近似散乱点集上优势较明显，同时在保护分片稀疏度上效果更好，即每一层支集均不为空集且稀疏。相较于分片稀疏性的MLASSO算法，aP_ISS算法在运行效率上有明显的优势，MLASSO模型存在事先人工输入和调节多个正则化参数的缺陷，本文算法的自适应性保证了算法可以更快地运行，且 MLASSO算法近似的曲面效果远不如本文算法。P_ISS算法的主要缺陷在于删除机制中参数C的选取依赖数据、噪音等因素，需要花费大量时间，而本文算法不仅避免了参数的选取而且能够得到和 P_ISS算法同等的近似效果。

另从表1～3的结果还可以观察到，分片稀疏逼近的目的是为了在每一层上都有非零元素表示，且是稀疏表示，本文算法除了近一步改进已有的分片算法 P_ISS，更重要的是为了通过“分片符号一致性”来体现分片稀疏的思想。实验结果表明本文的算法不仅在拟合效果上更好，并且达到了分片稀疏表示的效果。

表1 观测函数f1对应曲面拟合的数值结果

表2 观测函数f2对应曲面拟合的数值结果

表3 观测函数f3对应曲面拟合的数值结果

图1 观测函数f1对应4种算法拟合出的近似曲面的对比图

图2 观测函数f2对应4种算法拟合出的近似曲面对比图

图3 观测函数f3对应4种算法拟合出的近似曲面对比图

4 结 束 语

本文利用 aP_ISS处理散乱点曲面拟合问题,通过引入分片稀疏性，可以有效地保护在PSI空间中多层支集的分片稀疏性；进一步通过对分片逆尺度空间系统的分片符号一致性的考虑，避免了分片算法中参数的选取问题。实验结果表明，该算法近似散乱点曲面效果较好，验证了利用稀疏优化算法处理散乱点曲面拟合问题的优势。

分片稀疏思想应用到散乱数据拟合等问题仍然欠缺较为完善的研究，通过对稀疏优化算法的自适应分片处理来求解曲面拟合问题，将是未来研究的重点。