正方形中的那些事*

广东省深圳实验学校初中部()

1 正方形中的垂直结构

例1 如图1，已知正方形ABCD中，点E,F,G,H分别在边AB,CD,AD,BC上，若EF ⊥ GH，判 断EF与GH的数量关系.

图1

教学片段

教师：正方形给我们的第一印象是“方正”，这种感觉是由正方形中的“垂直结构”所保证的.正方形的对角线不仅有“互相垂直”的位置关系，还有“相等”的数量关系，那么对于一般的垂直结构，有类似的结论吗?

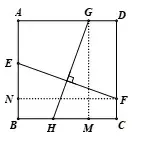
图2

生1：可以过点G作GM ⊥BC，过点F作FN ⊥ AB，证明ΔGMH∽= ΔFNE.(图2)

教师：很好，还有别的证法吗？

生2：还可以过点D作DP//GH，过点C作CQ//FE，证明ΔDCP=∽ ΔCBQ.(图3)

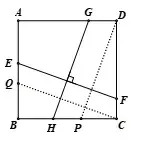
图3

教师：通过“作垂直”或“作平行”的方法，构造全等三角形，得到结论：两条互相垂直的直线被正方形对边截得的线段长相等.

例2如图4，将边长为12的正方形ABCD折叠，使得B点落在边AD上的P点，若折痕_EF的长为13，求线段PD的长.

图4

解析识别折叠问题中的垂直结构：PB ⊥EF，得到PB=EF=13,则AP=5,故PD=7.

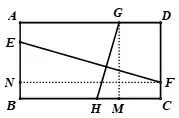
图5

方法提炼还可以将正方形中的垂直结构推广到矩形(图5)中，由ΔGMH∽ΔFNE，得：

2 正方形中的45°

例3如图6，正方形ABCD边长为2，点E,F,G,H分别是在边AB,CD,AD,BC上，且EF与GH的夹角为45°，若EF=求GH的长.

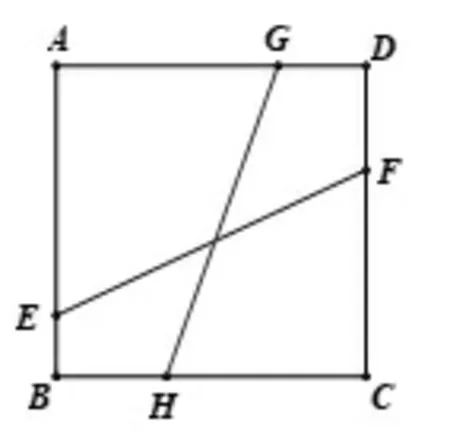
图6

教学片段

教师：除了90°角，正方形常常还与45°角相结合，如：对角线平分一组对角、半角模型等.

生3：仿照例1的作法，将线段EF和GH平移到点B处(即过点B作BM//EF,BN//HG)，则：∠MBN=45°,可构造半角模型.(图7)

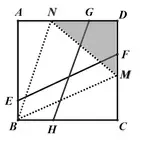
图7

例4(例2 变式)如图4，将边长为12的正方形ABCD折叠，使得B点落在边AD上的P点.

教学片段

教师：我们回到前面的折叠问题，在这个例题中，存在45°角吗？提出你的猜想.

生4：连接BH,猜想：∠PBH=45°.(图8)

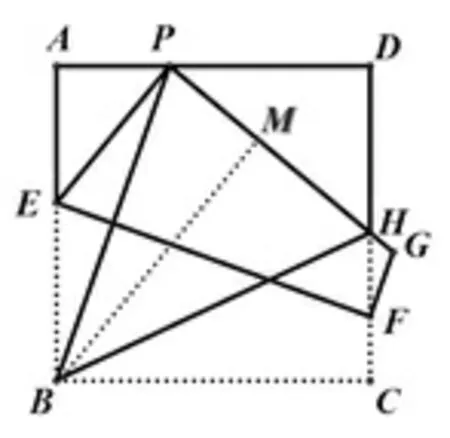
图8

教师：如何证明呢？小组成员互相讨论.

生5：小组讨论得：先证PB平分∠APH,再作BM ⊥PH,证明：ΔBAP∽= ΔBMP,ΔBCH∽= ΔBMH.

解析因为∠EPB=∠EBP,AD//BC.所以∠BPH=∠PBC=∠APB.易证：ΔBAP∽= ΔBMP(AAS)，ΔBCH∽= ΔBMH(HL).所以45°.

教师：除了∠PBH为定值外，题目中还有“变化中的不变量”吗？

生6：ΔPDH的周长始终为定值24.

方法提炼(半角模型)在正方形ABCD中，若∠EBF=45°，则有：1○EF=AE+CF； 2○EB平分∠AEF； 3○FB平分∠EFC等结论.(图9)

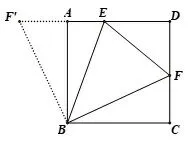
图9

3 正方形中的√

例5 如图10，正方形ABCD中，点E是BA延长线上一点，连接DE，点F在DE上且DF=DC，DG ⊥CF,DH平分∠ADE交CF于点H，连接BH.(1)若DG=2,求DH的长；(2)求证：

图10

教学片段

生7：有！∠GDH=∠GDF-45°,故：DH=

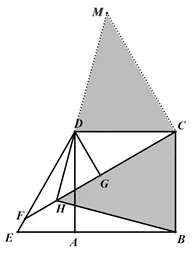
图11

生8：利用隐藏的45°角∠DHG,将CH作为直角边构造等腰直角三角形.

解析作CM ⊥ CH交HD延 长 线于M，证明：ΔCHB∽= ΔCMD.所以由：MD+DH=MH,即：

图12

方法提炼涉及正方形中的问题，往往通过其中隐藏的45°角，构造等腰直角三角形，结合“旋转变换、一线三等角”等策略解决问题.(图12)

4 正方形中的旋转变换

例6如图13，正方形ABCD中，对角线AC,BD相交于点E，以点E为顶点作正方形EFGH，使点A,D分别在EH和EF上，连接BH,AF.(1)判断并说明BH和AF的数量关系；(2) 如图14，将正方形EFGH 绕点E顺时针方向旋转θ(0° ≤θ ≤360°)，设AB=a,EH=b,且a ＜2b.连接AG，设AG=x，直接写出x的取值范围；若四边形ABDH是平行四边形，补全图形，并求a与b的数量关系.

图13

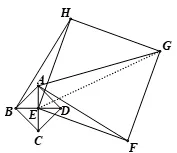
图14

图15

教学片段

生9：对于 (1)利用正方形的性质，证明ΔEBH∽= ΔEAF，即可得到：BH=AF.

生10：连接EG，则EG的长度始终不变.

生11：如图15，补全图形，由四边形ABDH是平行四边形，则AH始终等于BD.

解析(2)：在ΔAEG中，利用三角形的三边关系，得：：由AH=BD，即得：

方法提炼正方形有天然的“等线段，共顶点”，为构造旋转创造了条件，对于这样的动态类问题，往往抓住“变化中的不变量”，以不变应万变.

5 正方形中的特殊四边形

例7如图16，正方形ABCD中，E是CF上一点，四边形BEFD是菱形，求∠BEF的度数.

教学片段

教师：小组合作，充分挖掘正方形与菱形的性质，提供多样性的解法.

生12：(法1) 如图16，连接AC交BD于点O，作EG ⊥BD.则：2EG=2CO=AC=BD=BE，而EG ⊥BD,即：∠EBG=30°,故：∠BEF=150°.

图16

生13：(法2) 如图17，延长DC使得CM=CD，连接BM,EM，延长BC交EM于点N.易证：∠ECB=∠ECM=135°,则ΔECB∽= ΔECM.则EB=EM=BD=BM,即 ΔEBM为 等 边 三 角 形，故：∠BEC=30°，故：∠BEF=150°.

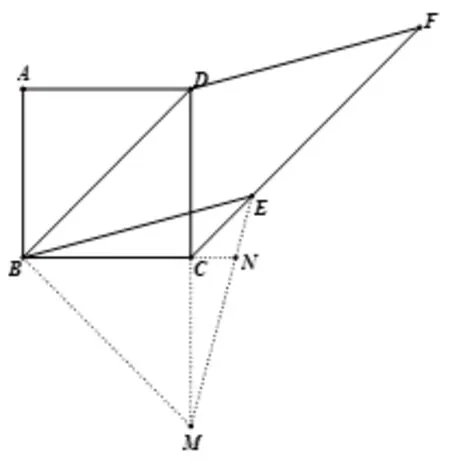
图17

生14：(法3)如图18，以BC为斜边构造等腰直角三角形ΔBPC，取BE中点Q,连接PQ.因为∠PCF=45°+90°+45°=180°,所以P,C,F三点共线，则BE=2PQ，又 因为BD=所以BE=BD=2BP,故：BQ=PQ=BP,即ΔBPQ为等边三角形，故：∠BEF=60°+90°=150°.

图18

……还有更多解法，进一步延续到了课外.

数学教学应以理解、探究、问题解决为价值取向，追求数学素养的达成，并促进学生核心素养的发展.四边形的复习课一直是初中数学教学的难点，而既有一般平行四边形的性质，又兼具菱形、矩形性质的“正方形”，更是中考的重中之重，尤其需要教师站在系统的高度，追根溯源，引发学生主动体验、探索、思考、提炼，真正提高学生的思维水平和问题解决能力.