基于预测原理的回声状态网络在线盲均衡算法

杨凌，韩琴，程丽，赵傲男，杜娟

（兰州大学信息科学与工程学院，甘肃 兰州 730000）

1 引言

通信系统中，由于信道的非理想特性，接收机接收到的信号会产生严重的畸变，通常采用均衡技术尽可能地恢复失真信号。传统的自适应均衡需要发送训练序列以提供均衡器所需的监督信号，对于时变信道，需要频繁发送训练序列以达到实时跟踪信道的目的，不仅降低了通信系统的信息传输速率，而且加大了信息传输成本。1975 年，Sato[1]首次提出了盲均衡的概念。盲均衡技术不需要发送训练序列，仅仅利用接收序列本身的先验信息，便可自适应地调整均衡器参数，跟踪信道特性，完成对信号的最佳估计[2-3]。

Bussgang 类盲均衡算法应用较广泛，它将构造的代价函数的极小值对应于理想系统，并通过自适应算法得到相应的极小值，继而得到系统参数[4-7]。该类算法稳定性强，但存在收敛后剩余误差较大、易陷于局部最小等缺点。考虑到传输序列由独立随机变量组成，文献[8]提出了基于预测原理的盲均衡思想，利用二阶统计量调整线性预测误差滤波器结构的参数，并以此消除失真信号中存在的冗余，但有限长的线性预测误差滤波器存在自身结构的局限性，很难获得理想的均衡效果。由于非线性系统能产生高阶统计量信息，文献[9]用非线性的模糊滤波器代替传统的线性结构，降低了均衡误码率。文献[10]首次提出将神经网络作为非线性预测误差滤波器实现盲均衡的方法，随后，前馈神经网络如径向基函数（RBF,radial basis function）[11]网络、多层感知器（MLP,muti-layer percetron）[12]、极限学习机（ELM,extreme learning machine）[13]，以及递归神经网络如回声状态网络（ESN,echo state network）[14-15]相继用于构造非线性预测误差滤波器。其中，前馈神经网络各层神经元之间无反馈，非线性映射能力弱于递归神经网络，对非线性信道的均衡效果较差。文献[14-15]选用只需要训练输出权值的新型递归神经网络ESN[16-17]作为非线性预测误差滤波器，在非线性信道下获得了较理想的均衡性能。然而，文献[14-15]中的实验仅针对BPSK 调制信号的盲均衡，没有涉及抗噪声能力强且可充分利用通信带宽的正交幅度调制（QAM,quadrature amplitude modulation）信号，此外，文献[14-15]的算法均采用数据批处理方式进行盲均衡，对于时变信道，不能有效地实时跟踪信道变化。

本文针对非线性信道的QAM 信号，采用复数型回声状态网络[18]作为非线性预测误差滤波器，用递归最小二乘算法计算网络的输出权值，实时跟踪信道变化，并通过自动增益控制（AGC,automatic gain control）和旋转因子分别调整信号的幅值和相位旋转，提出了基于预测原理的回声状态网络在线盲均衡算法（ESN-PEF,echo state network-prediction error fitter）。

2 问题描述

2.1 基于预测原理的盲均衡方法

基于预测原理的盲均衡框架如图1 所示。其中s(n)是发送序列，h 是发送序列通过的信道，是信道输出序列，v(n)是高斯白噪声序列，x(n)是加噪信道输出序列，Z-1是单位延迟，P 是预测误差滤波器，y(n)是加噪信道输出序列的预测值，e(n)是预测误差，g 是AGC 装置，是恢复的发送序列。

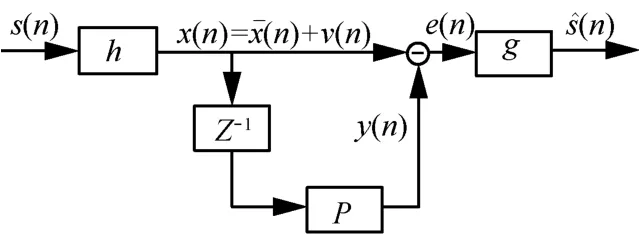
图1 基于预测原理的盲均衡框架

设发送序列 s(n)通过式(1)所示的信道，即

其中，Lh是信道阶数，hi是信道系数。

则加噪信道输出序列可以表示为

由图1 可知，预测误差为

其中，X(n-1)=[x(n-1),x(n-2),…]T，P(·)表示预测误差滤波器。

设预测误差滤波器为

其中，Lw是滤波器阶数。

则预测误差可以扩展为

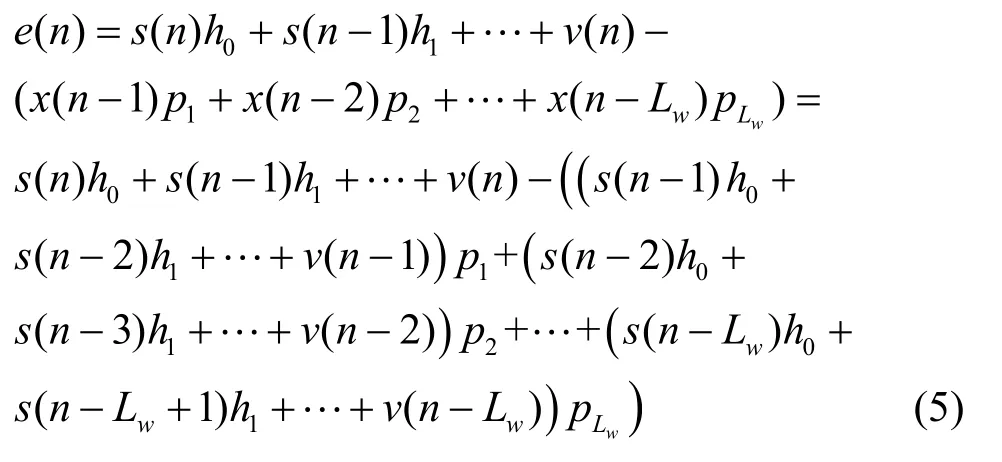
整理式(5)，可得

理想的均衡结果是只保留s(n)h0，消除其他冗余项，然后通过AGC 调整幅值得到原始发送序列的估计。

由于有限长的线性滤波器不可能在保留s(n)h0的同时使其他冗余项的系数为0，因此很难获得理想的均衡效果。为尽可能地消除冗余项的影响，一般的做法是增加线性预测误差滤波器的阶数Lw，但Lw的增加会带来较大的计算量，且性能的提升也非常有限。考虑到非线性结构能产生高阶统计量信息且具有强大的非线性映射能力，文献[9]提出用非线性结构代替线性预测误差滤波器。

2.2 回声状态网络

回声状态网络是一种由输入层、动态储备池（隐含层）、输出层三部分组成的递归神经网络，其拓扑结构如图2 所示，其中L 是网络的输入节点数，M 是输出层节点数。

图2 回声状态网络的拓扑结构

储备池的状态更新和网络的输出计算式分别为

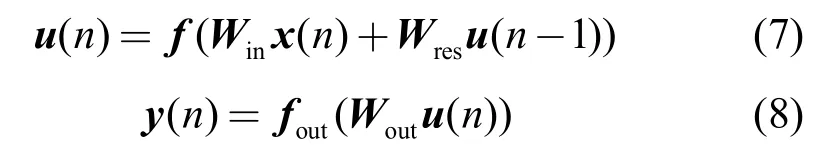
其中，x(n)=[x1(n),…,xL(n)]T是n 时刻网络的输入信号；u(n)=[u1(n),…,uN(n)]T是n 时刻的储备池状态；y(n)=[y1(n),…,yM(n)]T是n 时刻网络的输出信号；Win∈RN×L是输入权值矩阵；Wres∈RN×N是储备池内部连接权值矩阵；Wout∈RM×N是输出权值矩阵；f(·)=(f1(·),…,fN(·))是储备池内部神经元的激活函数，通常为非线性函数，其中N 是储备池神经元的节点数；fout(·)=(f1(·),…,fM(·))是网络输出层的读出函数，可采用线性读出和非线性读出2种形式。

ESN 的输入权值矩阵Win和储备池内部连接矩阵Wres随机生成且固定不变，不需要反复训练，唯一需要训练的是输出权值矩阵Wout，通常通过如式(9)所示的伪逆求解方式得到。

其中，T=[d(1),…,d(n)]T是目标向量，d(n)是n时刻网络的期望输出，H∈RN×n是储备池矩阵，H†表示矩阵的伪逆。

由上述分析可知，ESN 极大地简化了神经网络的学习过程，而且避免了梯度下降算法引起的局部最小问题，与传统的递归神经网络相比，其在利用大规模、稀疏连接的递归隐层提高映射能力的同时，仍保留了前馈网络的简单性原则，使网络具有较少的训练参数和较小的计算量。

3 ESN-PEF 算法描述

针对盲均衡问题，将ESN 作为图1 所示框架中的预测误差滤波器P，设置其输入节点和输出节点的个数均为1。对于QAM 信号而言，若选用实数型ESN，需分别处理信号的实部和虚部，这样忽略了信号实部与虚部之间的相互依赖性，无法得到最优的均衡性能，故本文选用激活函数、相关权值均为复数值的复数型ESN。考虑到实际通信中信道特性会随着工作条件的变化而变化，为达到实时跟踪信道变化的目的，本文采用递归最小二乘（RLS,recursive least square）法迭代计算ESN 的输出权值矩阵Wout，代替传统ESN 中通过求伪逆计算Wout的方式，构造了将ESN 作为预测误差滤波器的在线盲均衡算法，算法具体推导如下。

在图1 所示的盲均衡框架下，加噪信道的输出序列 x(n)为接收机的输入信号。本文将 x(n)设置为ESN 的期望输出，并将其单位时间延迟 x(n-1)作为ESN 的输入，网络迭代的目的是依据预测原理使ESN 的实际输出 y(n)无限逼近其期望输出 x(n)，即

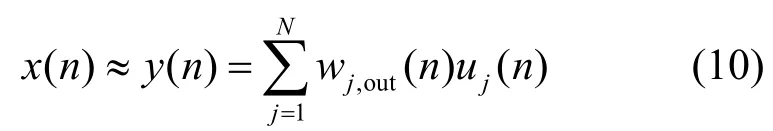
其中，wj,out(n)是ESN 输出权值矩阵Wout(n)的元素。为使网络的均方误差最小，需求解

式(11)是一个线性回归问题，可以等价为

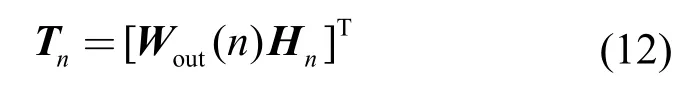
其中，Tn=[x(1),…,x(n)]T是n 时刻的目标向量，Hn∈RN×n是n 时刻的储备池矩阵。

式(12)可以看成一个有n 个等式的方程组，从中可以得到最小二乘解为

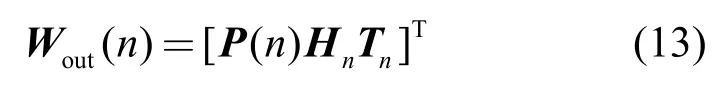
其中，有

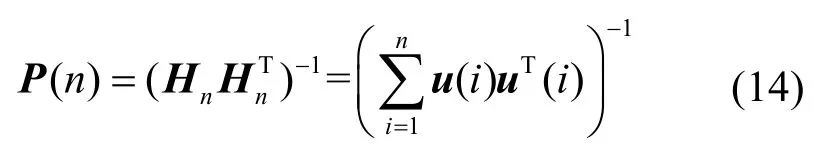
将式(13)展开可以得到

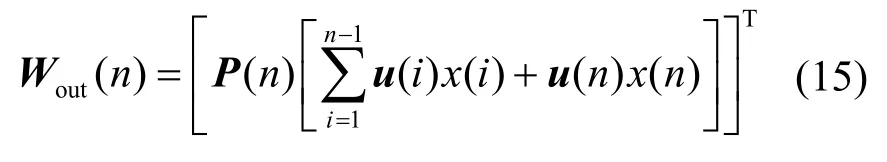
同理可得

由式(14)可得

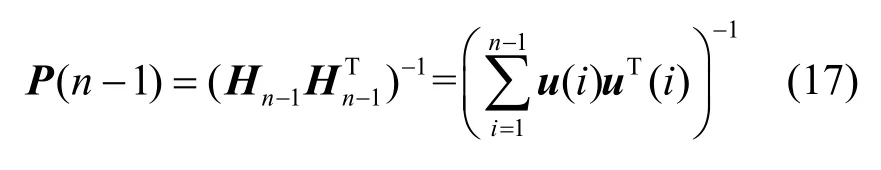
将式(16)和式(17)代入式(15)得

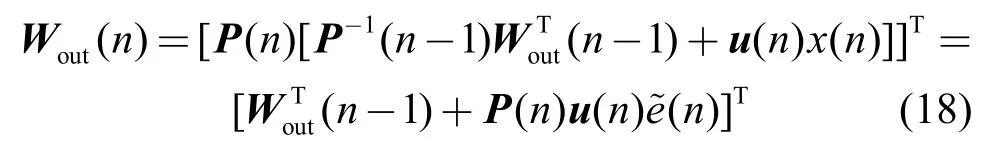
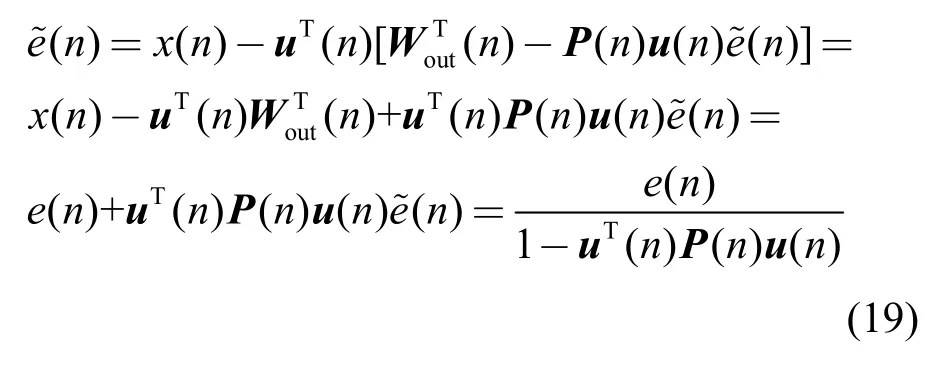
将式(19)代入式(18)得

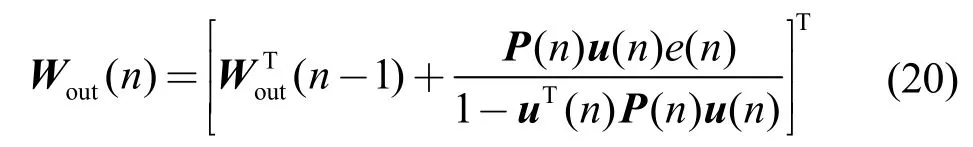
式(20)中的 P(n)可以根据式(14)和式(17)得到

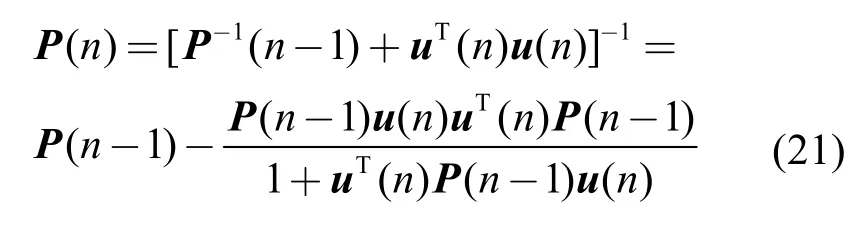
当Wout(0)和 P(0)已知时，可以通过式(20)在线更新ESN 的Wout(n)，进而计算ESN 的实际输出y(n)，使其逼近ESN 的期望输出 x(n)。然而，由于 x(n-1)中未包含n 时刻的发送序列信号 s(n)，因此 y(n)只能无限接近 x(n)中除s(n)h0项之外的冗余项，即 e(n)=x(n)-y(n)无限接近s(n)h0。

由于s(n)h0中仍存在未知的信道系数 h0，因此将 e(n)作为AGC 的输入序列，通过式(22)和式(23)调整信号的幅值

其中，b(n)是AGC 的输出序列；c(n)是AGC 的控制信号，其初始值设置为1；R 是用户自定义的电平；α＜1 是幅值加权因子。

由于AGC 只能解决幅值失真问题，而信道的非理想特性引起的QAM 信号的相位旋转问题无法解决，因此本文在图1 所示的AGC 装置后进行了相位调整，将AGC 的输出序列 b(n)与旋转因子exp(j a(n))相乘，最终得到发送信号 s(n)的估计。

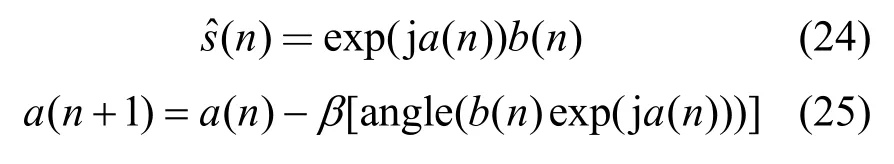
其中，a(n)表示相位，其初始值设为0；β＜1 表示相位加权因子；angle(·) 表示相位。

由以上推导可知，针对非线性信道，本文将复数型ESN 作为非线性预测误差滤波器，采用递归最小二乘迭代训练方式，在不需要发送序列s(n)的情况下，仅利用均衡器接收序列 x(n)，实现了QAM 信号的盲恢复。为方便叙述，将上述在线盲均衡算法简记为ESN-PEF，具体流程如算法1 所示。

算法1ESN-PEF 算法流程

4 实验仿真

为充分验证本文提出的ESN-PEF 算法的有效性和性能优势，本节设计了3 组仿真实验，第一组实验探究不同的ESN 参数设置对算法的影响及均衡后的星座图；第二组实验在非线性信道下，从收敛速度、均方误差（MSE,mean square error）、算法复杂度三方面比较了本文算法与其他基于预测原理的盲均衡算法的均衡性能；第三组实验验证ESN-PEF 算法对信道的跟踪性能。

实验平台设置如下，CPU 为Intel(R)Core i7-7700 3.6 GHz，Windows10 64 bit，Matlab R2015b。

在3 组实验中，发送序列 s(n)均为随机生成且满足独立同分布的16QAM 信号，所加噪声均为0均值的高斯白噪声。ESN 的Win、Wres和储备池状态的初始值 u(0)随机生成，输出权值的初始值Wout(0)设置为全0 向量，AGC 的控制信号的初始值c(0)设置为1，相位的初始值 a(0)设置为0，幅值调整和相位调整的加权因子α 和β 分别设置为0.001和0.000 5。为了确保网络的稳定性，本节设置ESN储备池神经元连接权值Wres的谱半径ρ(Wres)=0.9。算法的评判标椎为均方误差，计算式为

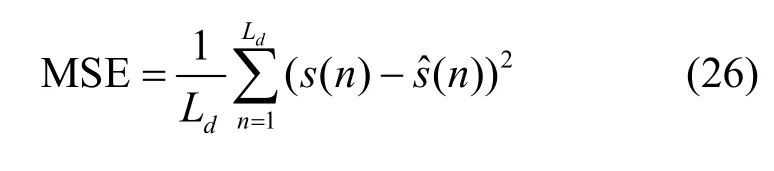
其中，Ld表示数据长度。

4.1 ESN 参数设置对算法性能的影响

本组实验通过选取不同的储备池规模N、神经元激活函数 f(·) 和读出函数 fout(·)来验证不同的ESN 参数设置对ESN-PEF 算法性能的影响。实验针对式(26)所示的非线性信道为

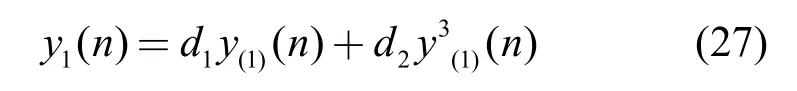
其中，y(1)(n)=0.762 5 +0.1538z-1+0.076 9z-2，系数d1、d2确定了由信道引起的非线性失真程度。

表1 给出了在不同信噪比SNR 下，储备池规模N 对算法MSE 值的影响。由表1 可以看出，在不同的信噪比下，随着储备池规模N 的增大，算法的MSE 值基本不变，当N 增大到50 时，MSE 值反而有增加的趋势，这说明N 的增大并不能达到降低MSE 值的目的。

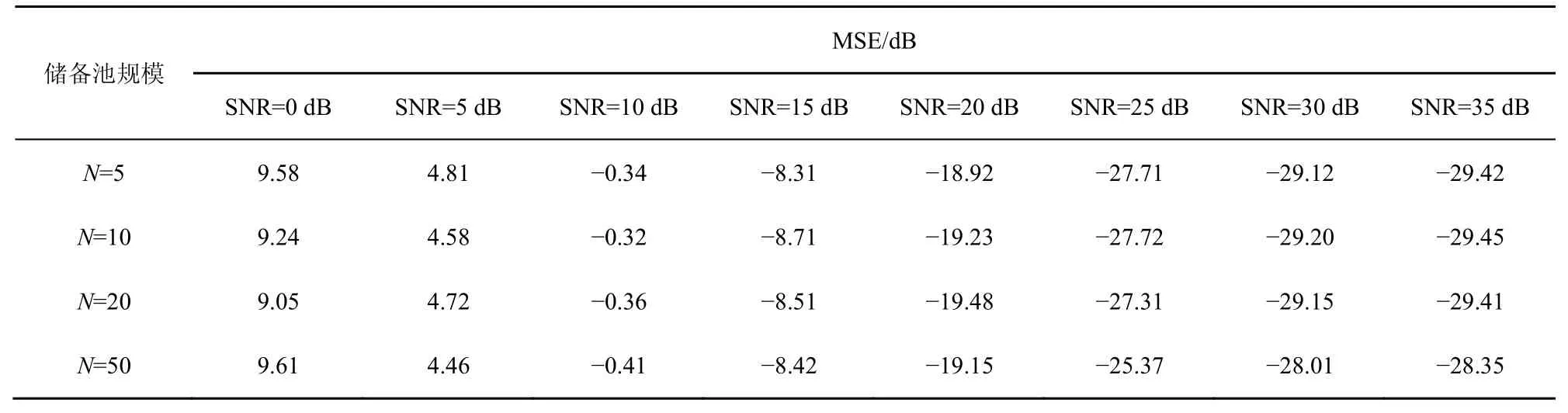
表1 不同信噪比下，不同储备池规模N 对ESN-PEF 算法MSE 值的影响

表2 给出了当SNR=30 dB 时，不同储备池规模N 对算法收敛速度的影响。当N 分别为5、10、20时，算法均在迭代2 000 次左右收敛；当N 为50时，算法在迭代5 500 次左右收敛，收敛速度明显变慢。因此，即使增大N 也不能使算法的性能提升。

表2 SNR=30 dB 时，不同储备池规模N 对ESN-PEF算法收敛速度的影响

考虑到较大的N 值会增大算法的计算复杂度，且并不能有效地提升算法的均衡性能，故在以下的实验中，均设置储备池规模N=5。

表3 给出了储备池规模N=5 时，不同信噪比下，不同激活函数 f(·) 对算法MSE 值的影响。由表3可以看出，在不同的信噪比下，使用tanh(·) 和sinh(·)作为激活函数时，两者的MSE 值相差不大，但使用tribas(·) 作为激活函数时，其MSE 值在信噪比大于15 dB 之后明显高于其他2 种激活函数。

表3 N=5 时，不同信噪比下，不同激活函数 f(·) 对ESN-PEF 算法MSE 值的影响

表4 给出了储备池规模N=5，SNR=30 dB 时，不同激活函数 f(·) 对算法收敛速度的影响。由表4可以看出，使用tanh(·) 和sinh(·) 作为激活函数时，算法均在2 000 次左右收敛，而选取tribas(·) 作为激活函数时，算法收敛速度变慢，大约迭代5 000次后收敛，所以为保证算法的性能优势，应选择合适的激活函数。

表4 N=5，SNR=30 dB 时，不同激活函数f(·)对ESN-PEF 算法收敛速度的影响

表5 和表6 给出了当N=5，激活函数为tanh(·)时，不同的输出层读出函数 fout(·) 对算法性能的影响。实验中 fout(·) 分别取线性和非线性的读出函数，其中，线性读出函数 fout(·)=1，非线性读出函数fout(·)=g(y)+jg(y)，g(y)=y+φsin(πy)，φ=0.4。

表5 N=5，激活函数为tanh(·) 时，不同信噪比下，读出层函数对ESN-PEF 算法MSE 值的影响

表6 N=5，激活函数为tanh(·)，SNR=30 dB 时，读出层函数对ESN-PEF 算法收敛速度的影响

表5 给出了不同信噪比下，读出层函数对算法MSE 值的影响。由表5 可以看出，选择非线性读出函数可以得到更小的MSE 值，当SNR=30 dB 时，选择非线性读出函数均衡的MSE 值比选择线性读出函数均衡的MSE 值降低了15 dB 左右，所以读出层函数的选取对算法的MSE 值有较大的影响。表6 分析了当SNR=30 dB 时，读出层函数的选择对算法收敛速度的影响。由表6 可以看出，无论选取线性读出函数还是非线性读出函数，算法均在2 000 次左右收敛，因此读出层函数的选择对算法的收敛速度无影响。

图3 给出了当N=5，激活函数 f(·) 为tanh(·)，SNR=30 dB 时，16QAM 信号均衡前后的星座图。图3(a)是发送信号的星座图，图3(b)是均衡前的星座图，可以看出均衡器接收端的信号存在着严重畸变。首先选择线性读出函数，图3(c)给出了算法进行相位调整之前的均衡星座图，可以看出此时幅值已经被调整，星座图较清晰，但存在相位旋转问题。图3(d)是经过相位调整后的均衡星座图，可以看出，因信道引起的相位旋转问题已基本解决。图3(e)是非线性读出函数的均衡星座图，与使用线性读出函数的图3(d)相比，图3(e)星座图更加清晰紧凑，较好地恢复出了图3(a)所示的发送信号。

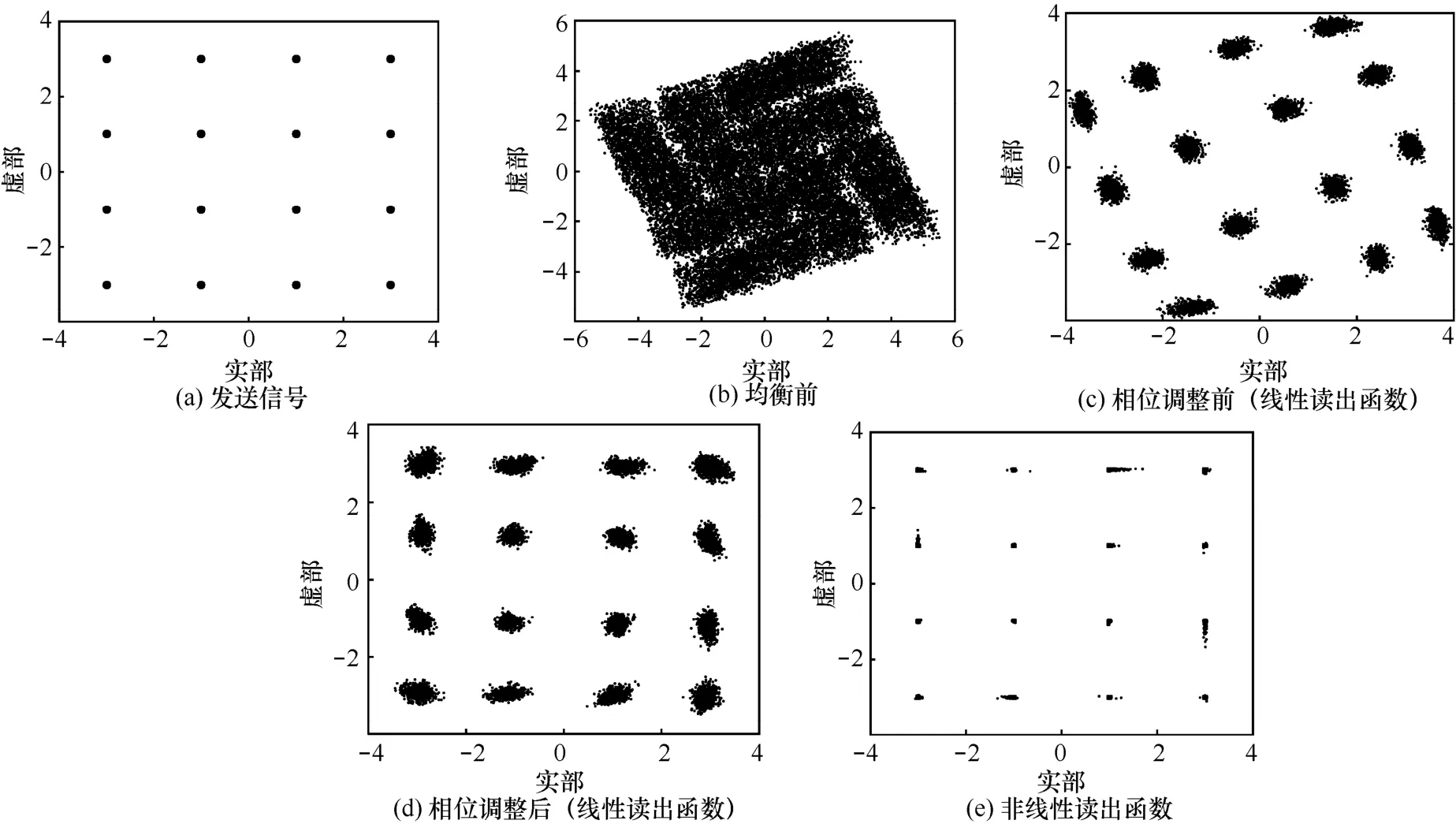
图3 16QAM 信号均衡前后的星座图

4.2 与其他基于预测原理盲均衡算法的性能对比

本组实验分别在2 种不同的非线性信道下，将本文提出的ESN-PEF 算法与线性预测误差滤波器（Linear-PEF）以及 MLP 作为预测误差滤波器（MLP-PEF）的盲均衡算法进行性能比较。实验所用非线性信道1 如式(27)所示，非线性信道2 如式(28)所示。

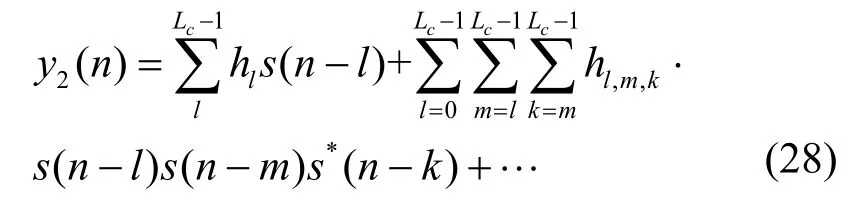
式(28)是用Volterra 级数构建的非线性记忆卫星信道，其中，hl,hl,m,k表示Volterra 级数的系数，第二项有一个共轭输入信号和2 个非共轭输入信号，Lc表示记忆深度。

实验中，设置均衡器接收机的SNR=30 dB，ESN-PEF 算法中，ESN 的储备池规模N=5，内部神经元的激活函数为tanh(·)，输出层的读出函数为fout(·)=g(y)+j g(y)，g(y)=y+φsin(πy)，φ=0.4，均衡器初始化设置与4.1 节相同。Linear-PEF 算法中，滤波器的阶数Lw=20，MLP-PEF 算法中，网络的输入层节点数为1，隐层节点数NMLP=20，输出层节点数为1，MLP 网络输出层同样采用上述非线性读出函数。

图4 和图5 分别在非线性信道1 和非线性信道2下，比较了Linear-PEF、MLP-PEF 和ESN-PEF 这3 种算法的性能。图4(a)和图5(a)描述了在不同的信噪比下，3 种算法的MSE 值曲线，可以看出，ESN-PEF 算法均衡后的 MSE 值明显小于Linear-PEF 算法和MLP-PEF 算法的MSE 值，当SNR=30 dB 时，ESN-PEF 算法均衡后的MSE 值比Linear-PEF 算法降低了20 dB 左右，比MLP-PEF算法降低了8 dB 左右，这说明与Linear-PEF 算法和MLP-PEF 算法相比，本文提出的ESN-PEF 算法在降低MSE 值方面具有较大的优势。图4(b)和图5(b)描述了3 种算法的收敛曲线，其中，Linear-PEF算法在2种信道下均在14 000次左右收敛，MLP-PEF 算法分别在4 000 次和5 000 次左右收敛，ESN-PEF 算法均在2 000 次左右收敛，这说明ESN-PEF 算法具有最快的收敛速度。

在非线性信道下，本文提出的具有良好非线性映射能力的ESN-PEF 算法仅需要5 个储备池神经元，便可获得更低的MSE 值和更快的收敛速度。相较于采用线性结构和前馈神经网络，MLP 作为预测误差滤波器的盲均衡算法，具有更强的去冗余项能力和更快的学习速率。

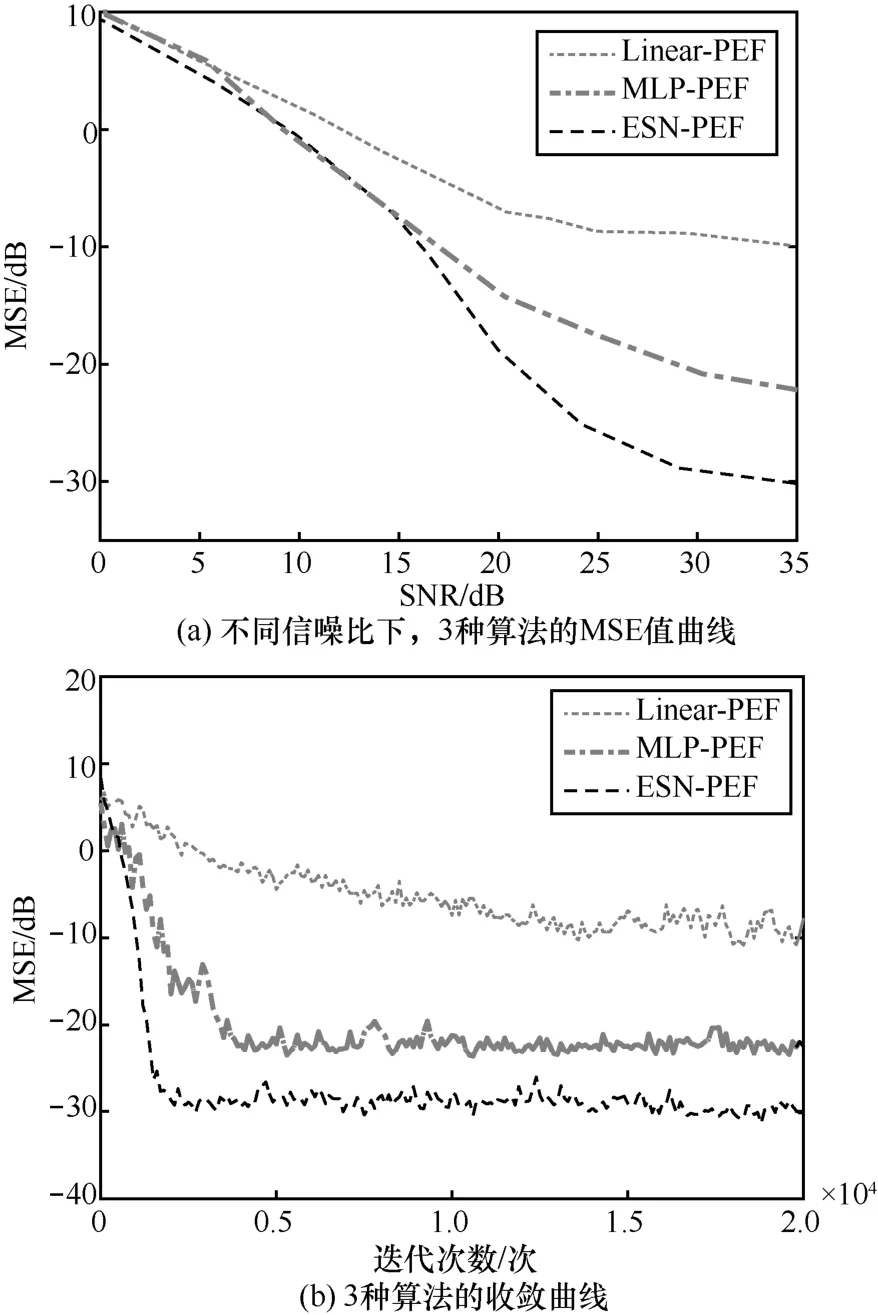
图4 非线性信道1 下的性能对较

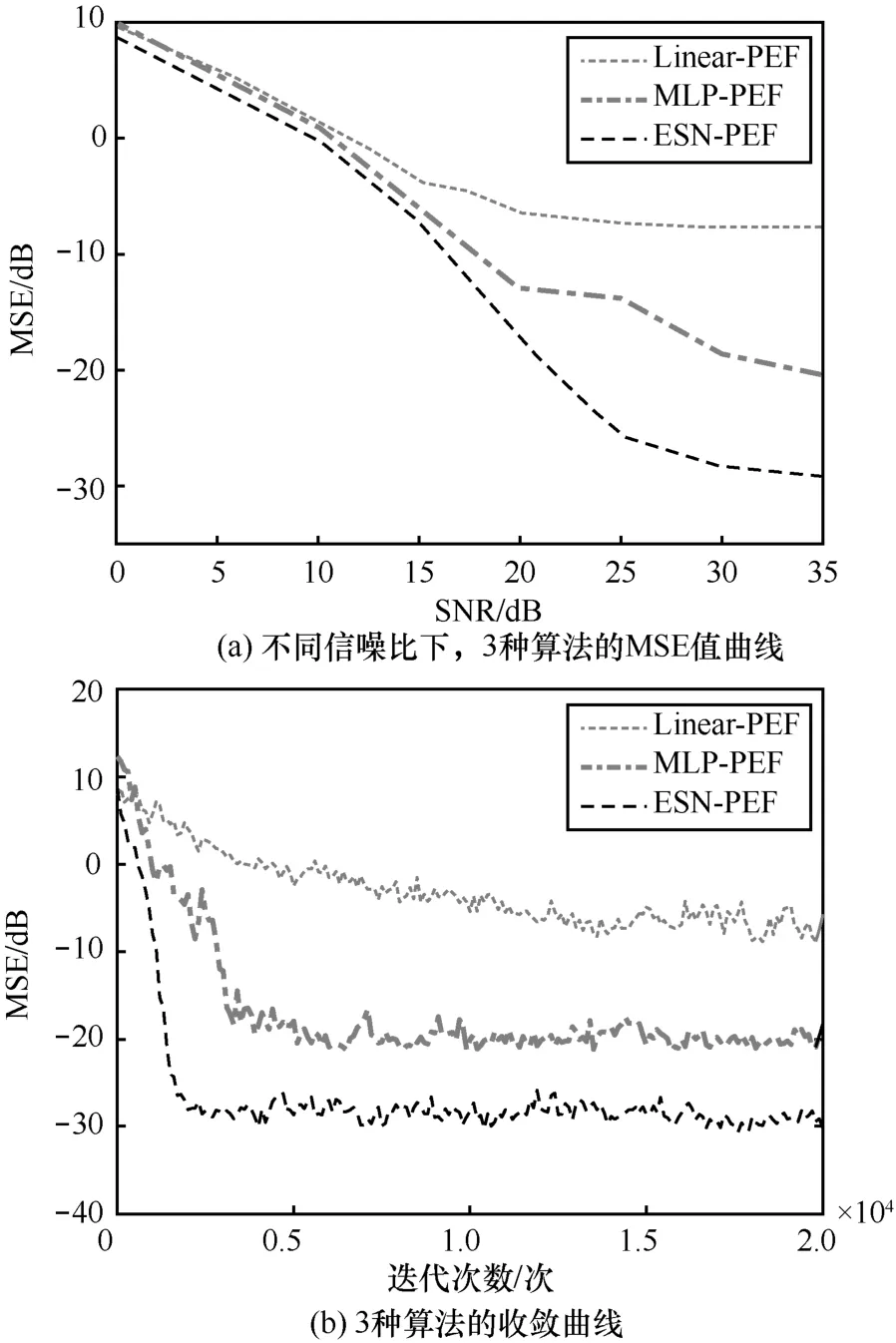
图5 非线性信道2 下的性能比较

表7给出了3种算法一次输出所需的计算复杂度[19]。其中，ESN-PEF 算法一次输出的计算复杂度可从算法1 中得到。算法1 的步骤3)～步骤6)运用了较多的矩阵乘法，其计算复杂度分别为O(N2+6 N)、O(N)、O(N3+3N2+2 N)、O(2N2+2 N)；步骤7)～步骤9)涉及的计算复杂度均为常数，每次计算记为O(1)，因此得到ESN-PEF 算法的计算复杂度为O(N3+6N2+11N +5)。从表7 中可得，ESN-PEF算法与Linear-PEF 算法相比，运用了较多的矩阵乘法，所以在降低MSE 值、加快收敛速度的同时，不可避免地增加了计算复杂度。ESN-PEF 算法与MLP-PEF 算法相比，虽然前者复杂度的最高阶大于后者，但由于MLP 所需隐含层节点数目NMLP大于ESN 的储备池规模N，因此，ESN-PEF 算法的计算复杂度低于MLP-PEF 算法的计算复杂度。

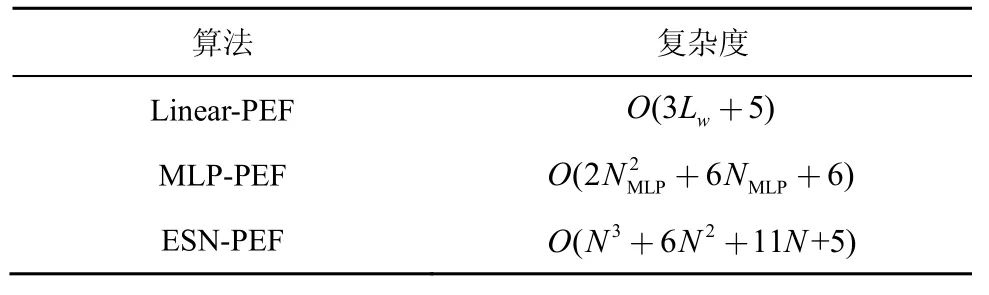
表7 Linear-PEF 算法、MLP-PEF 算法与ESN-PEF算法的复杂度比较

4.3 信道跟踪性能

文献[14-15]将ESN 作为预测误差滤波器进行盲均衡时需要批量处理数据，不能实时跟踪信道变化。本文提出的ESN-PEF 算法用递归最小二乘法训练获得最小预测误差，可以有效弥补上述不足。为验证ESN-PEF 算法的信道跟踪性能，本节采用非线性信道2 设置如下两组实验：1)使用三阶Volterra 级数构造卫星信道，当迭代次数达到10 000 次后更换Volterra级数的系数hl,hl,m,k，实现信道的切换；2)首先使用三阶Volterra 级数构造信道，当迭代次数达到10 000次后，切换到五阶Volterra 级数构造的信道。

图6 是ESN-PEF 算法的信道跟踪曲线。从图6(a)中可以看出，ESN-PEF 算法在迭代2 000 次左右后第一次收敛，当三阶Volterra 级数建模信道的系数改变后，算法迭代大约1 000 次后再次收敛，这说明ESN-PEF 算法具有迅速跟踪信道变化的性能，可适用于时变信道。从图6(b)中可以看出，由三阶Volterra 级数建模信道切换为五阶Volterra 级数建模信道后，算法迭代1 500 次后再次收敛，进一步说明即使信道发生较大的改变，ESN-PEF 算法仍具有良好的跟踪性能。

图6 ESN-PEF 算法的信道跟踪曲线

5 结束语

本文针对非线性信道下的QAM 信号，采用复数型回声状态网络作为非线性预测误差滤波器，用递归最小二乘算法迭代计算网络的输出权值，实时跟踪信道变化，并通过自动增益控制和旋转因子分别调整信号的幅值和相位旋转，提出了基于预测原理的回声状态网络在线盲均衡算法。仿真实验表明，与线性预测误差滤波器结构以及MLP 作为预测误差滤波器的盲均衡算法相比，本文提出的算法无论是在MSE 值，还是在收敛速度上均具有一定的性能优势，且能够快速跟踪信道变化。