自由半群和斜积映射下的拓扑压*

王威 李渊

(南通理工学院基础教学学院，南通，226002；南京师范大学数学科学学院，南京，210023)

1 引言

拓扑压是热力学公式系统中一个非常重要的概念，Ruelle[1]首先提出该概念并证明了拓扑压的变分原理，其考虑的是紧致不变集合相对于一个同胚的势函数的拓扑压.Walters[2]将此概念进行推广，系统地介绍了关于熵和拓扑压的一些概念和性质.

1999年，Bufetov[3]给出了自由半群作用下的拓扑熵的定义，并得到了在斜积映射下的乘积定理.2011年, Ma[4]研究了半群作用下的拓扑熵和拓扑压.2019年王威[5]利用紧致化的方法构造了任意拓扑空间的拓扑压.近年来，各种集合上的拓扑压文献很多，比如[6-8], 经典的拓扑压介绍可以查看[9].本文将[3]中拓扑熵推广至拓扑压，获得压工作的新进展，并在斜积映射下获得新的乘积定理.

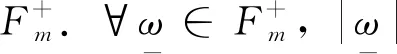
记∑m是由符号0,1,…,m-1构成的双边无限序列的全体，即

∑m={ω=(…,ω-1,ω0,ω1,…):∀i∈Z+,ωi=0,1,…,m-1}.

∀ω1,ω2∈∑m, 记d(ω1,ω2)=2-k, 其中k=inf{|n|:ω1≠ω2}.

设一个有m个生成子的自由半群作用在X上, 这m个自由生成子映射记为f0,f1,…,fm-1.假设这些映射都是连续的.

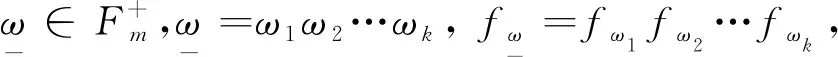
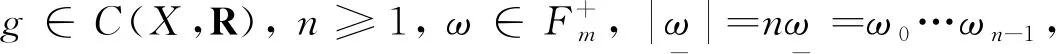
2 相关定义和性质

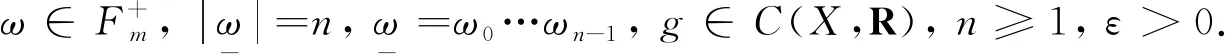
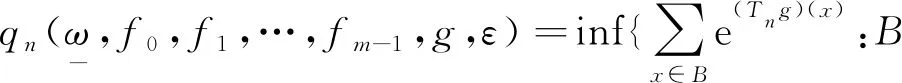
我们有如下性质：

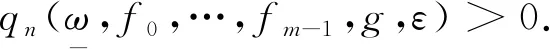
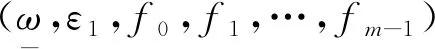
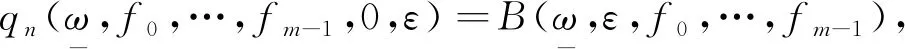
定义2设g∈C(X,R),ε>0, 定义

我们有下述性质：

(4)Qn(f0,…,fm-1,0,ε)=B(n,ε,f0,…,fm-1).

(5) 若ε1>ε2, 则Qn(f0,…,fm-1,g,ε1)≤Qn(f0,…,fm-1,g,ε2).

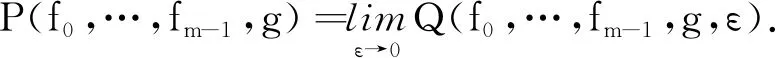
映射P(f0,…,fm-1,·)：C(X,R)→R∪{∞}称为自由半群作用下的拓扑压. 它与自由半群作用下的拓扑熵h(f0,…,fm-1,g,ε)有下列关系：

(6)P(f0,…,fm-1,0)=h(f0,…,fm-1,g,ε).

下面从分离集角度给出一个等价定义.

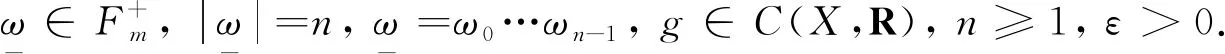
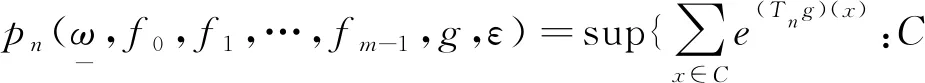
性质：

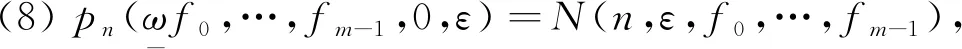
定义4设g∈C(X,R)，ε>0. 定义

性质：

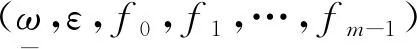
3 主要定理及证明

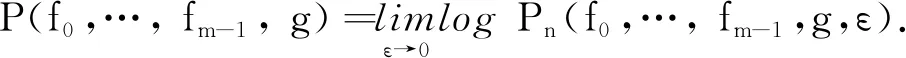
证明由性质(11)知上述极限存在. 由性质(9), 有

由引理1, 对任意δ>0有

因此

证毕.

我们称P(f0,…,fm-1,g)为自由半群作用下的拓扑压.

下面将斜积映射与自由半群的作用结合起来.

映射F:∑m×X→∑m×X定义为:F(ω,x)=(δω,fω0(x)). 当ω0=0时,fω0=f0；当ω0=1时,fω0=f1; 依此类推.

设g1和g2分别为∑m和X上的连续函数. 则g=g1×g2是∑m×X上的连续函数. 令g(ω,x)=g1(ω)+g2(x),∀(ω,x)∈∑m×X.

定理2映射F的拓扑压满足:

P(F,g)=P(δ,g1)+Pn(f0,…,fm-1,g2).

+g(fωn-2…ω0(x))),

因此

从而

即

P(F,g)≥P(δ,g1)+Pn(f0,…,fm-1,g2).

+g(fωn-2…ω0(x))),

因此

从而

进而

P(F,g)≤P(δ,g1)+Pn(f0,…,fm-1,g2).

证毕.