部分变换半群与全变换半群之间的同态*
林双 杨秀良
(1.江苏省新沂市瓦窑中学高中部,新沂,221400;2.杭州师范大学理学院,杭州,310036)
1 引言
集合X上的所有部分变换的集合称作是X的部分变换半群,记作PTX;集合X上的所有全变换的集合称作X的全变换半群, 记作TX;集合X上的所有部分单变换的集合称作是X的对称逆半群, 记作ISX. 它们上的运算都是映射的合成(本文规定合成运算从右到左). 本文讨论X是有限的情况,即X是基为自然数的集合. 不妨设X=N= {1,2,…,n}.这时PTX,TX和ISX分别记作PTn,Tn和ISn.
1997年,Schein 和Teclezghi[1]研究了ISn的所有自同态. 随后在 1998 年,他们在[2,3]中又分别讨论了Tn和PTn的自同态. 2009年, Ganyushkin 和Mazorchuk 在 [4]中讨论自同态时提出了一个公开问题:描述从S到T的所有同态(单同态,满同态),其中S,T∈{PTn,Tn,ISn}. 本文描述了PTn与Tn之间的所有同态.
2 主要结果
设半群S代表PTn或Tn.半群S的所有自同构的集合记作Aut(S),集合N上的置换群记作Sn,群Sn的所有自同构的集合记作Aut(Sn).当n≠4时,S4除了有正规子群S4,A4和E4外,还有一个正规子群K,称作Klein四元群.
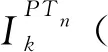
对任意的x∈N,ax={(x,x)}表示PTn中秩为1的幂等元,即
其中ax(i)=Ø表示i不属于ax的定义域,即i∉dom(ax),i=1,2,…,x-1,x,x+1,…,n.
0x表示PTn或Tn的常量变换,即
0表示PTn的空变换,即
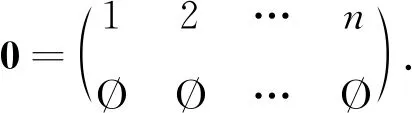
本文的主要结论如下:
定理1设n≠4.选取ε,δ∈Tn使得ε3=ε且εδ=δε=δ2=δ.定义Θε,δ:PTn→Tn如下:
则Θε,δ是PTn到Tn的一个同态.若ε2=ε=δ,则Θε,δ是一个常量同态,即Θε,δ把PTn映到Tn的一个幂等元δ.若ε2=ε≠δ,则Θε,δ是一个秩为2的同态,即Θε,δ把PTn映到Tn的一个半格{ε,δ},满足δ<ε.若ε≠ε2≠δ,则Θε,δ是一个秩为3的同态,即Θε,δ把PTn映到Tn的一个半群{ε,ε2,δ},其中δ是零元,{ε,ε2}是Tn的一个子群.
反之,当n≠4时,PTn到Tn的每个同态都具有以上形式.对于n=4,PT4到T4除了有以上的同态外,还具有同态σπ,π∈S4,其定义如下:
K4在S4中的每个陪集恰包含H4中的一个元素.若α∈S4,设σ(α)∈K4α∩H4是这个元素;若α∈PT4S4,设σ(α)=04,则σπ定义为:对任意的α∈IS4,σπ(α)=πσ(α)π-1.
定理2设n≠4.
(i)设π∈Sn.对任意的α∈Tn,定义Λπ(α)=παπ-1,则Λπ是Tn到PTn的一个同态.
(ii)选取ψ∈Aut(Sn).定义Ωψ:Tn→PTn如下:
则Ωψ是Tn到PTn的一个同态.
(iii)选取ε,δ∈PTn使得ε3=ε且εδ=δε=δ2=δ.定义Θε,δ:Tn→PTn如下:
则Θε,δ是Tn到PTn的一个同态.若ε2=ε=δ,则Θε,δ是一个常量同态.若ε2=ε≠δ,则Θε,δ把Tn映到PTn的一个半格{ε,δ},满足δ<ε.若ε≠ε2≠δ,则Θε,δ把Tn映到PTn的一个半群{ε,ε2,δ},其中δ是零元,{ε,ε2}是PTn的一个子群.
(iv)选取π∈Sn,i,j,z∈Xn.定义Ψπ:Tn→PTn如下:
则Ψπ是Tn到PTn的一个同态.
反之,对于n≠4,Tn到PTn的每个同态都具有形式(i)-(iv).对于n=4,T4到PT4除了有以上的同态外,还具有同态Υπ,π∈S4, 其定义如下:
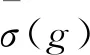
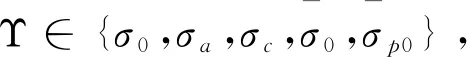
3 定理的证明
定理1的证明需要用到以下引理.
引理1([4])n≥1,Tn中不包含任何元素α使得对任意γ∈Sn满足γα=α.
定理1的证明设φ是PTn到Tn的同态. 若n=1,则φ(PTn)={(1)}=T1,其中元素(1)表示恒等变换,因此φ是常量同态.
以下设n>1. 考虑三种情况:φ在Sn上是单的;φ在Sn上是非单的且n≠4;φ在Sn上是非单的且n=4.
若φ在Sn上是单的,则Sn≃φ(Sn),进而|φ(Sn)|=n!.由于φ(Sn)是N的某个子集Y的置换群,其中Y=im(ε),ε是φ(Sn)的单位元,因此n!=|φ(Sn)|≤|Y|!,进而Y=N,φ(Sn)=Sn.
对任意γ∈Sn,存在η∈Sn使得φ(η)=γ.由于η0=0η=0,因此,
γφ(0)=φ(0)η=φ(0).
由引理1知,φ(0)不可能是Tn中元素,故φ在Sn上不可能是单的.
若φ在Sn上非单且n≠4,则φ具有形式Θε,δ.若φ在Sn上非单的且n=4时,则φ具有形式σπ.再按[2]同样的讨论即可证定理1成立.
下面来证明定理2. 为此,先给出下面几个引理.
引理2([4]) 设S表示Tn,ISnTn,ISn或PTn之一.设ε是S的一个幂等元.则
(i)S的包含ε的一个极大子群Gε为
Gε={α∈S:im(α)=im(ε),ρα=ρε}.
(ii) 若rank(ε)=k,则Gε≌Sk.
证明(i)略.
(ii) 设幂等元
显然对任意的i有ti∈Bi.设Sk是集合{t1, …,tk}上的置换群.Gε中任意一个元素g都具有下面的形式
其中ti1,…,tikti1,…,ti2是t1,…,tk的一个排列.定义映射
显然φ是一个双射. 经验算可知φ保持运算, 故φ是同构.
引理3设S,T∈{Tn,ISn,PTn},且设φ是S到T的同态,φ在Sn上是单的,则φ(Sn)=Sn且φ|Sn∈Aut(Sn).
证明由于φ在Sn是单的,因此φ(Sn)≅Sn,且φ(Sn)是T的一个子群,进而φ(Sn)包含在T的某个极大子群中.由引理2知T的所有极大子群都同构于Sk,k≤n,而且同构于Sn的极大子群只有Sn本身,因此φ(Sn)=Sn,且φ|Sn∈Aut(Sn).
引理4设Xn={1,2,…,n},k是一个正整数且1≤k≤n,则下列结论成立:
(i) 若k>n/2,则Xn中任意两个k-子集的交非空.
(ii) 若k≤n/2,令E是满足下列条件的Xn的若干个k-子集组成的集合:
A=B或A∩B=Ø(A,B∈E),
则|E|≤n/k.
证明(i) 显然.

引理5设n,k为正整数.
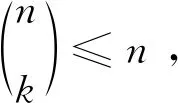

证明(i) 由于
即
(n-1)(n-2)…(n-k+1)≤k!=k(k-1)…2·1,
故k=n-1.

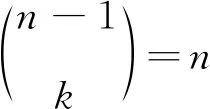
定理2的证明容易验证(i)-(iii)及(v)成立.下面验证Ψπ是同态.设φ=π-1Ψπ(α)π.则
因此只需证明φ是同态.

其中{x1,…,xn}={y1,…,yn}={z1,…,zn}=Xn,则
由于
因此φ是同态.
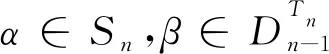
其中{x1,…,xn}={y1,…,yn}={z1,…,zn}=Xn.易验算φ是同态.
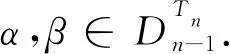
dom(φ(α))∩im(φ(β))=Ø,
进而φ(α)φ(β)=0,因此φ保持运算.
若rank(αβ)=n-1,则α在im(β)上是单的. 设
则x1和x2只有一个在im(β)中.不妨设x1∈im(β).设
经验算知φ保持运算.
反之,设φ是Tn到PTn的同态.若n=1,则φ(T1)={1n},或φ(T1)={0},因此φ是形式(ii)中的常量同态.
下面讨论n>1.考虑三种情形:φ在Sn上是单的;φ在Sn上是非单的且n≠4;φ在Sn上是非单的且n=4.
情形1若φ在Sn上是单的,则由引理3知φ(Sn)=Sn.对任意γ∈Sn,存在η∈Sn使得φ(η)=γ.对任意的a∈Xn, 0aη=0a,进而φ(0a)φ(η)=φ(0a),因此φ(0a)γ=φ(0a),故φ(0a)=0或φ(0a)=0ta,ta∈Xn.
情形1.1设φ(0a)=0ta,ta∈Xn,映射π:Xn→Xn为π(a)=ta.则φ(0a)=0ta=0π(a).对任意的α∈Tn,α0a=0α(a),进而有
0π(α(a))=φ(0α(a))=φ(α0a)=φ(α)φ(0a)=φ(α)0π(a)=0φ(α)(π(a)),
因此π(α(a))=φ(α)(π(a)),故π(α)=φ(α)(π).
下面证明π是单的.对任意x,y∈Xn,对任意γ∈Sn,γ(x),γ(y)都可取遍Xn.若π(x)=π(y),则
π(γ(x))=φ(γ)(π(x))=φ(γ)(π(y))=π(γ(y)).
因此或者x=y,进而π是单的;或者π是常量映射,进而存在b∈Xn使得π=0b.由于对任意α∈Tn有π(α)=φ(α)(π),因此0bα=φ(α)0b,进而0b=φ(α)0b,由此得φ(α)(b)=b.而φ(α)可取遍Sn,因此Xn={b},这与n>1矛盾.
由于π是有限集合上的单射,因此π是双射,进而π,π-1∈Sn.由于π(α)=φ(α)(π),因此φ(α)=παπ-1=Λπ,故φ∈Aut(Tn).

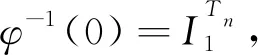
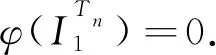
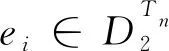
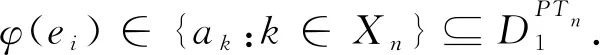
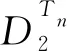

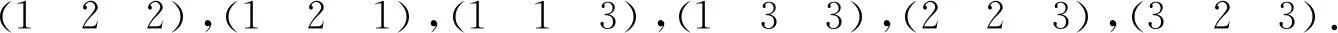
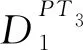
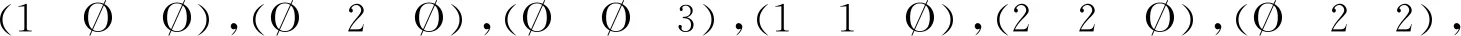
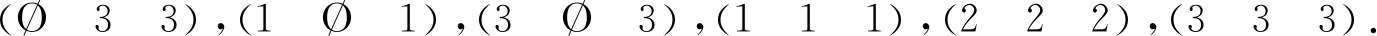
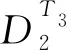
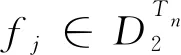

e2,e3,…,en和f1,f3,…,fn.
由于{φ(ei):i∈I}和{φ(fj):j∈J}都有n-1个元素,因此存在ki∈I,kj∈J使得φ(eki)=φ(fkj).而eki,fkj的值域不同,因此eki,fkj不在≡S2的同一个同余类中,矛盾.故φ不存在.
情形1.2.2若m=n,则φ-1(0)=Tn,这与φ在Sn上是单的矛盾.
情形1.2.3若m=n-1,则φ|Sn是Sn的自同构且φ(TnSn)=0.故φ具有形式(ii).

(1)
对任意不同的i,j∈J,记Yij=im(ei)∩im(ej),则im(ej)Yij⊆Xnim(ei).由于ei,ej在Yij上的限制都是恒等变换,因此它们的积eiej在Yij上的限制也是恒等变换,进而有
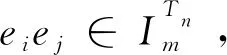
φ(eiej)=φ(ei)φ(ej)=0,
于是
dom(φ(ei))∩im(φ(ej))=Ø.
(2)
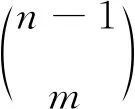
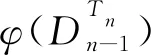
|im(φ(e1))|=…=|im(φ(en-1))|=l,

由(2)式可得
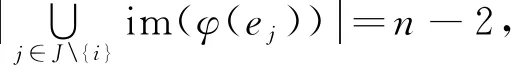
下面分两种情况进行讨论.
情况A对任意的i∈J,设|dom(φ(ei))|=1.则φ(ei)∈{a1,a2,…,an}.从En中选取具有形式(1)的幂等元en,由x的任意性可得φ(en)∈{a1,a2,…,an},故
{φ(e1),φ(e2),…,φ(en)}={a1,a2,…,an}.
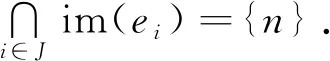
从En中选取幂等元
则有


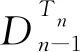
(3)
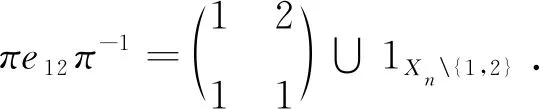
下面讨论i0,j0的情况.

φ′(πe12π-1)=φ′(e12).
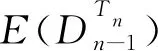
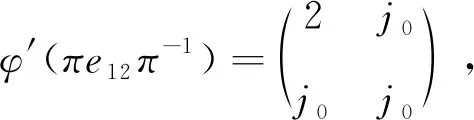
这显然不成立,矛盾.

这显然不成立,矛盾.

其中x1,…,xn,z1,z3,…,zn∈Xn.
设Sn中置换
则α=π2e12π1-1.因此
设
则
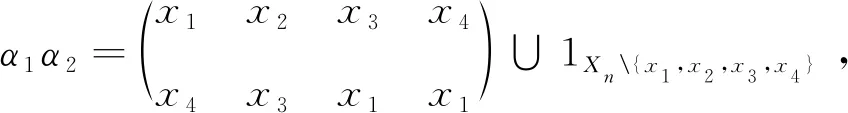
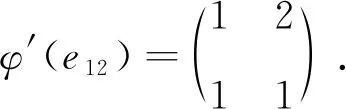
因此φ=πφ′π-1=Ψπ.
若n=6,则S6的自同构中有6!个内自同构. 若φ在S6上的限制是S6的内自同构,则同前面证明一样可证φ=Ψπ.下设φ在S6上的限制是S6的外自同构.S6有6!个外自同构[5],[6].S6可由生成元(12),(13),(14),(15),(16)生成.定义映射
φ:(12)→(12)(36)(45), (13)→(16)(24)(35), (14)→(13)(25)(46),
(15)→(15)(26)(34), (16)→(14)(23)(56),
则φ是S6的一个外自同构.S6的外自同构集合为{φΛπ:Λπ∈Inn(S6),π∈S6}.设φ′=φΛπ-1在S6上的限制为φ,φ′(e12)=e0.
对于α∈Tn,定义α的中心化子为集合CSn(α)={π∈Sn:απ=πα}.则
{π∈Sn:π(1)=1,π(2)=2}⊆CSn(e12).
取{π∈Sn:π(1)=1,π(2)=2}中的任意对换(ij),设φ′((ij))=(i1i2)(i3i4)(i5i6),其中i,j∈{3,4,5,6}, {i1,i2,i3,i4,i5,i6}=X6.由于(ij)e12=e12(ij),两边作用φ′得
(i1i2)(i3i4)(i5i6)e0=e0(i1i2)(i3i4)(i5i6).
(4)
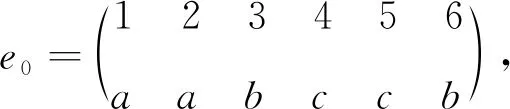
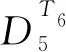
设rank(e0)=1.若a=1,b,c∈{Ø},则(4)式无解,矛盾. 同理讨论其他情况可知都是不成立的.
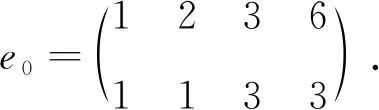
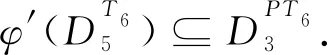
情形2φ在Sn上不是单的且n≠4.此时φ具有形式(iii),同[7]中定理证明的情况2讨论即可.
情形3φ在Sn上不是单的且n=4.此时φ具有形式(iv),同[7]中定理证明的情况3讨论即可.
定理2得证.
从定理2易得
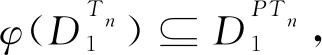
——卡文迪什测定万有引力常量

