2019年高考全国卷Ⅱ文科数学第21题的五种解法
甘志国
(北京市丰台二中 100071)
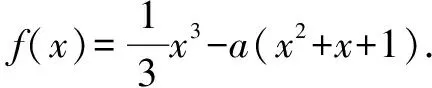
(1)若a=3,求f(x)的单调区间;
(2)证明:f(x)只有一个零点.

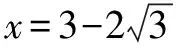
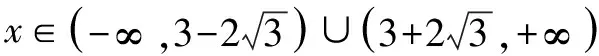

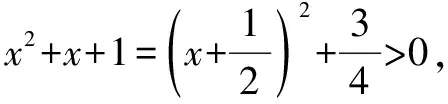
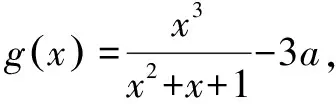
因而g(x)至多有一个零点,即f(x)至多有一个零点.
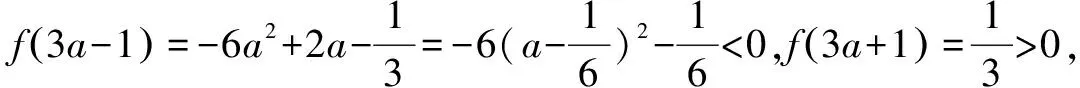
解法2 可得f′(x)=x2-2ax-a,其判别式Δ=4a(a+1).
可得3f(x)=x2(x-3a)-3ax-3a.
当x-3a≥1即x≥3a+1时,由x2≥0,可得
3f(x)≥x2-3ax-3a=x(x-3a)-3a.
又当x≥0,即x≥max{0,3a+1}时,可得
3f(x)≥x-3a≥1,
f(x)>0.
设x=-t,可得-3f(x)=t2(t+3a)-3at+3a.
当t+3a≥1即t≥1-3a也即x≤3a-1时,由t2≥0,可得
-3f(x)≥t2-3at+3a=t(t-3a)+3a.
又当t≥max{0,3a+1}即x≤min{0,-3|a|-1}时,可得-3f(x)≥t+3a≥1,
f(x)<0.
因而f(x)存在零点.
①当Δ≤0即-1≤a≤0时,f(x)是增函数,进而可得函数f(x)有且只有一个零点.
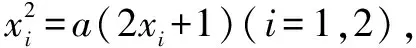
得三次函数f(x)的极大值与极小值同号,因而f(x)有且只有一个零点.得欲证结论成立.
解法3 可得f′(x)=x2-2ax-a,其判别式Δ=4a(a+1).
当x>max{1,9|a|}时,可得
0 a(x2+x+1)≤|a|(x2+x+1)≤3|a|x2, -a(x2+x+1)≥-3|a|x2. 当x 所以0 a[t2+(1-t)]≥-|a|[t2+(1-t)]≥-|a|t2. -a[t2+(1-t)]≤|a|t2. 因而f(x)存在零点. 又因为“题(2)的解法2”中已证得三次函数f(x)的极大值与极小值同号,所以f(x)有且只有一个零点.得欲证结论成立. 所以g(3a-1)<0 解法5 可得 3(x-1)f(x)=x3(x-3a-1)+3a①. 在①中设x=-t,可得-3(t+1)f(-t)=t3(t+3a+1)+3a -3(t+1)f(-t)=t3(t+3a+1)+3a>t3+3a>0,f(-t)<0,所以f(x)有零点. 由“题(2)的解法1”中证得的g(x)在(-∞,+∞)上单调递增,可知f(x)至多有一个零点. 综上所述,可得f(x)有唯一零点.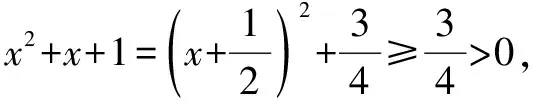
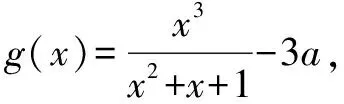

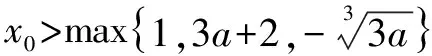

——2018年全国高考Ⅲ理科数学21题别解

