非晶合金电机振动噪声特性分析与实验研究

陈 健，吴胜男

(沈阳工业大学 国家稀土永磁电机工程技术研究中心，沈阳 110870)

0 引 言

非晶合金作为一种新型的导磁材料，具有高磁导率、低矫顽力、高饱和磁密、低损耗等特点。国内外一些科研机构和公司已经采用非晶合金取代传统的硅钢片制作电机的铁心，使铁心损耗和温升大幅降低。但非晶合金材料存在磁致伸缩效应，极易引起定子铁心的振动和噪声[1-2]。

目前，永磁电机振动噪声的研究主要针对硅钢片电机。文献[3]基于ANSYS与SYSNOISE软件对电机的噪声联合仿真。文献[4]对高功率密度永磁电机的振动和噪声进行研究。文献[5]对分数槽永磁同步电机电磁振动进行分析。文献[6]利用模态叠加法分析电机振动和噪声。文献[7]采用开辅助槽的方法对汽车爪极发电机电磁振动进行削弱。文献[8]对大型电机铁心振动特性仿真分析。

非晶合金材料对振动噪声影响的研究正处于起步阶段，国外已有少量研究。2000年，比利时Koen Delaere等对磁致伸缩导致电气装置的振动噪声进行研究，利用磁力耦合有限元方法获得磁致伸缩材料特性[9]。2006年英国帝国理工大学博士Anouar Belahcen基于虚功原理结合有限元方法建立磁弹性耦合方程，推导磁致伸缩力与磁场的关系[10]。2008年波兰的Jerzy Podhajecki等学者通过基于有限元算法的二维数值程序的编写，对无刷直流电机空载时由麦克斯韦力和磁致伸缩引起的振动进行了计算[11]。2011年韩国首尔国立大学Shin Pan Seok基于虚功原理结合磁弹性有限元方法推导了关于形变和磁场的关系，对3kW无刷直流电机的磁致伸缩力和振动模态进行模拟计算[12]。相对国外，非晶合金电机振动噪声的研究在国内仍是一个较新的课题，河北工业大学祝丽花博士与沈阳工业大学吴胜男博士进行了相关研究工作，并取得了一定的成果[13-14]。

综上所述，国内外尚未有文献将非晶合金电机与硅钢片电机的振动噪声进行对比分析。本文以2台结构和参数完全相同，定子铁心选用不同材料的永磁电机作为研究对象。采用解析计算和有限元仿真两种方法，得到了振动噪声的数值及其分布，并与测试结果进行了对比，验证了本文所提方法的有效性和仿真结果的正确性。同时总结了定子铁心材料对永磁电机振动噪声的影响规律，为低振动噪声永磁电机的设计提供了理论依据。

1 振动噪声解析法分析

永磁同步电动机内部，定转子磁场相互作用产生电磁力fe，定子铁心磁化时产生磁致伸缩力fm。这两个力共同作用，使定子铁心和机座随时间周期性变形，即定子发生振动，是电机电磁振动噪声的主要来源。

1.1 电磁力的计算与分析

根据麦克斯韦定律，定子铁心内表面单位面积上的法向电磁力为

(1)

式中,μ0为真空磁导率，μ0=4π×10-7H/m；b(θ,t)为电机气隙磁密。

永磁电机的气隙磁场，不考虑铁心磁阻与饱和的影响，气隙磁密的表达式为

b(θ,t)=f(θ,t)λ(θ,t)

(2)

式中,f(θ,t)为气隙磁动势；λ(θ,t)为气隙比磁导。

永磁同步电动机气隙磁动势由气隙基波磁动势、定子绕组谐波磁动势和转子永磁体谐波磁动势三部分组成，其表达式为

式中,v为定子磁场谐波次数，每极每相槽数为整数槽时，v=(6k1+1)p，k1=±1，±2，±3…；μ为转子磁场谐波次数，μ=(2k2+1)p，k2=0，1，2，3…。

永磁同步电动机定子有齿槽而转子为表面式永磁体结构时，气隙比磁导分为不变部分与周期分量两部分，其表达式为

(4)

式中,z为定子槽数；Λ0为气隙平均磁导幅值；Λk为k次谐波磁导幅值，k=1，2，3…。

将式(2)～(4)代入式(1)中，去掉那些振动阶数高、振动幅值小的电磁力波，同时去掉基波分量，因为它们不会产生振动和噪声，故电磁力为

(5)

1.2 磁致伸缩力的计算与分析

磁致伸缩引起的应变与磁场强度之间的关系通常用线性压磁方程来描述，其数学模型可以表示为

(6)

式中,ε为应变；E为杨氏模量；σ为应力；d为压磁系数；H为磁场强度。

对于定子铁心，式(6)中的应力σ即为磁致伸缩力fm，应变ε通常用磁滞伸缩系数λ表示，则式(6)可改写为

fm=Eλ-Edh

(7)

式中，E、d为常数，λ和H为变量。λ和H之间没有直接的关系，但可以通过中间变量B建立二者之间的联系，即绘制磁化曲线与磁滞伸缩曲线。

磁化曲线与磁致伸缩曲线均选择实验测试的方法。磁化曲线常用的测试方法为爱泼斯坦方圈和伏安法，由于伏安法的测试结果更接近电机的实际工况，本文采用伏安法进行测试。磁滞伸缩曲线参照国际电工委员会公布的IEC/TR 62581-2010标准进行测试，实验仪器选用德国进口的单片磁致伸缩特性测量装置。实验得到的曲线如图1和2所示。

图1 定子铁心磁化曲线

图2 定子铁心磁致伸缩曲线

1.3 振动噪声的计算与分析

将式(5)电磁力fe及式(7)磁致伸缩力fm的表达式代入，作用在定子铁心内表面的集中力为

Pre=2πRil1(fe+fm)

(8)

式中,l1为定子铁心长度；Ri为定子铁心内半径。

对于封闭式永磁电机，设定子铁心和机壳无相对切向位移，机壳和铁心一起振动且振幅相等，两者振动类似同一个刚体圆环，其刚度和质量分别等于机壳和铁心的刚度之和与质量之和，则根据机械阻抗理论，振动位移为[15]

(9)

式中,ω为振动角频率；K1、K2为铁心和机壳的刚度；m1、m2为铁心和机壳的等效质量。

将永磁电机视为有限长圆柱形辐射来计算电机产生的噪声，则永磁电机辐射的声功率为

(10)

式中,ρ为空气的密度；c为声波在空气中的传播速度；Sf为电机声辐射模型的表面积。

根据噪声理论，声功率级为

(11)

式中,W0为基准声功率，W0=10-12，单位为瓦。

由式(9)、式(11)及以上推导过程可知：永磁电机电磁振动噪声主要是由电磁力fe与磁致伸缩力fm共同引起的。电磁力fe的大小主要与电机的极槽配合有关，虽然非晶合金与硅钢片材料的磁化曲线有差异，但对电磁力的影响不大。磁致伸缩力fm受定子铁心磁密影响较大，当定子铁心磁密B=0.8～1.6T时，非晶合金磁致伸缩量是硅钢片的2倍。此外用作定子铁心的非晶合金材料比较薄，厚度仅为0.03mm，定子铁心叠压系数小，比硅钢片更容易发生振动。即使相同的力作用在定子铁心上，非晶合金比硅钢片定子铁心产生的振动噪声更大。

2 有限元验证与分析

本文以两台7kW永磁同步电动机作为研究对象，制作两台定转子尺寸完全相同，定子铁心分别采用硅钢片与非晶合金材料的样机。两台样机参数如表1所示。

表1 样机参数

振动噪声的有限元计算使用多物理场耦合分析软件COMSOL。在计算电磁场时，选用旋转机械-磁模块，旋转部分和定子接触处的边界设为连续。在计算机械振动时，选用固体力学模块，定子与机壳接触处的边界设为连续。仿真通过间接耦合的方式，使用旋转机械-磁模块计算得到定子磁密分布，调用磁致伸缩曲线，将这个形变设为初始应变，即可在固体力学模块计算时考虑磁致伸缩效应。电机振动位移与瞬态声压级云图分别如图3和4所示。

图3 电机振动位移云图

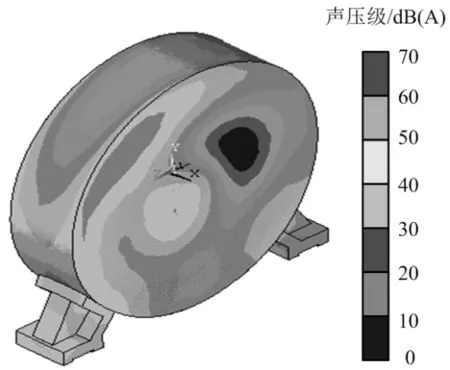
图4 电机声压级云图

为了研究电磁力和磁致伸缩力对电机振动噪声的贡献，分别将电磁力fe、磁致伸缩力fm、电磁力与磁致伸缩力之和fe+fm作为载荷，施加到7kW电机的3D有限元模型中，计算不同铁心材料引起振动加速度、振动速度、振动位移、噪声值的区别，如表2所示。

表2 振动和噪声有限元计算值

对比表2中的各数值可以得到，非晶合金电机电磁力产生的振动噪声比硅钢片电机大5%左右。非晶合金电机与硅钢片电机极槽配合相同，电磁力相等，5%的差别是由非晶合金材料容易振动导致的。非晶合金电机磁致伸缩力产生的振动噪声比硅钢片电机大20%左右。这是因为非晶合金材料的磁致伸缩作用明显，电机铁心磁密相同时，非晶合金磁致伸缩效应产生的形变比硅钢片大。

3 实验验证与分析

采用丹麦B&K公司的PULSE系统进行2台7kW样机的实验。振动测试选择4371型电荷加速度振动传感器。噪声测试选择2239型积分声级计。实验在消声室里进行，如图5所示，消声室的本底噪声为16dB(A)。

图5 振动和噪声测试现场

图6、图7分别为非晶合金电机与硅钢片电机振动加速度实测波形。

图6 非晶合金电机振动加速度

图7 硅钢片电机振动加速度

对比图6与图7，在每个时间周期内，硅钢片电机振动加速度接近正弦波，而非晶合金电机出现了一系列大小不同的峰值。这是因为硅钢片电机受磁致伸缩影响不大，振动加速度的波形与气隙磁密及电磁力近似；非晶合金电机磁致伸缩现象明显，在电磁力与磁致伸缩力共同作用下，振动时域信号中叠加了一系列不同幅值，不同频率的谐波成分。噪声与振动具有较强的相关性，波形与振动基本一致，本文不做详细分析。

非晶合金电机与硅钢片电机振动噪声有限元计算与测试值的对比如表3所示。通过表3中计算和测试值的比较说明，考虑电磁力和磁致伸缩力共同作用振动噪声的计算值与实际的大小基本相等，误差在5%以内，能够满足工程设计的要求。

表3 振动和噪声计算与测试结果对比

4 结 论

本文对定子铁心采用非晶合金与硅钢片材料的电机对比研究，推导了振动噪声的解析表达式，采用三维有限元软件分析了电机周围振动噪声的分布，并进行了相关实验，得出了以下结论：

(1)通过对振动噪声解析表达式的分析表明：电机极槽配合主要影响电磁力，定子铁心磁密主要影响磁致伸缩力，在电机设计时要综合考虑两种因素的影响才能设计出低振动噪声的非晶合金电机。

(2)对电机振动与周围声场进行了有限元分析，得出非晶合金电机电磁力产生的振动噪声比硅钢片电机大5%左右；磁致伸缩力产生的振动噪声比硅钢片电机大20%左右。振动噪声分析值与测试值相符，证明了该分析方法的可行性。

(3)测试了振动噪声的时域波形，非晶合金电机磁致伸缩效应明显，谐波含量比较丰富，导致振动噪声比硅钢片电机大。

综上，本文对设计阶段分析非晶合金电机振动噪声大小和分布规律具有重要的指导意义，为验证降低振动噪声的方案提供理论分析方法和依据。