缺失数据下MGINAR(p)模型的参数估计
杨艳秋, 王德辉
(1.吉林大学 数学学院, 长春 130012; 2.吉林师范大学 数学学院, 吉林 四平 136000)
在实际应用中, 一些随机事件会以一定的概率在一个观察周期内滞留或消失, 但又会在另一段时间内变得非常活跃, 可能引发更多的随机事件.例如: 某些犯罪案件, 通常具有衍生新的随机案件的可能, 其特征是能立即引起一个或多个其他案件的能力相对较小, 但相同情况一段时间后则会较明显.为了解决此类问题, 许多统计学者进行了相关研究[1-3].文献[1]提出了p阶混合整值自回归模型, 将两种主流算子二项稀疏算子和负二项稀疏算子以一定概率混合, 相比单一算子可以更好地拟合具有上述特征的数据.此外, 研究时间序列模型下缺失数据的参数估计方法有一定的应用价值.文献[4]给出了3种数据缺失机制, 分别为完全随机缺失、随机缺失和非随机缺失.本文在完全随机缺失机制下, 给出p阶混合整值自回归模型缺失数据的4种处理方法, 并给出每种方法下参数的条件最小二乘估计.
1 模型简介
文献[1]提出了二项稀疏算子与负二项稀疏算子以一定概率混合的p阶混合整值自回归模型(MGINAR(p)):



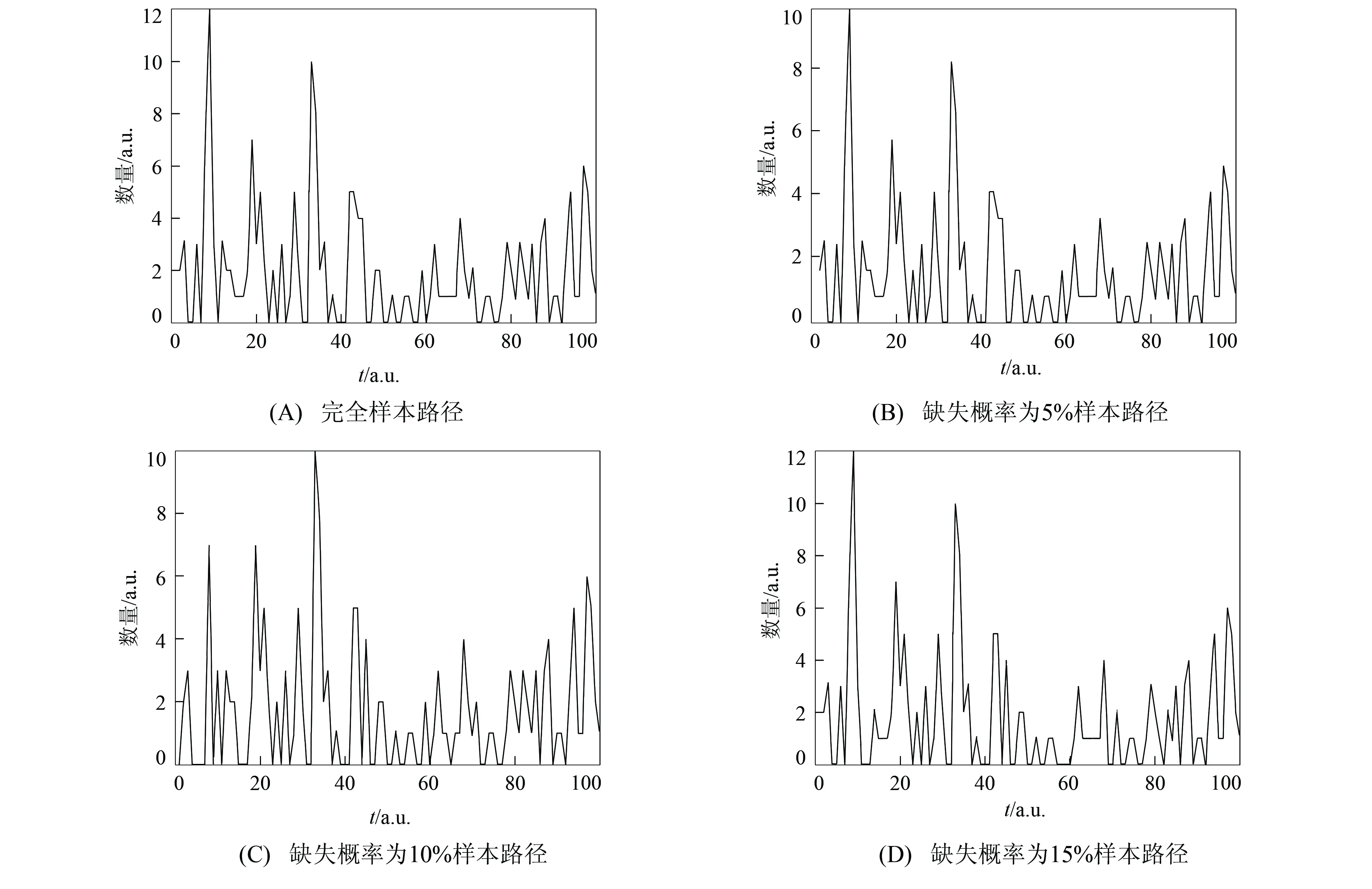
其中a 考虑来自MGINAR(p)模型的样本X1,X2,…,Xn, 其完全样本容量为n.该样本中观测到的数据为{Xs}, 其中s∈S⊂; 未搜集到的数据为{Xg},g∈G⊂(-S), 即为缺失数据.其中Xk1为第一个非缺失数据,Xkm为最后一个非缺失数据,Xk1与Xk2之间存在j个缺失数据, 共有m个非缺失数据, 共有(n-m)个缺失数据. 关于缺失数据的研究目前已得到广泛关注[5-7], 其中最简单直接处理缺失数据的方法是个案剔除法, 即将含有缺失数据的变量直接从数据中剔除.该方法是常用统计软件SAS(statistical analysis system)和SPSS(statistical product and service solutions)默认的处理方法, 本文基于p阶混合整值自回归模型研究该方法的可行性.采用个案剔除法, 将缺失数据剔除.但将个案剔除时, 会导致样本量的减少, 从而丢失部分数据信息, 进而在推断时会导致偏差较大, 使研究者忽略缺失数据前后数据间的相关结构. 考虑具有缺失数据时间序列模型的处理, 可通过最小二乘估计的思想求解缺失数据下时间序列模型的参数估计问题, 即可通过非插补条件最小二乘估计法, 最小化如下的完全平方和Q(θ)得到参数估计, 其中 (1) 基于MGINAR(p)模型, 有 且 通过迭代可求出式(1)中的E(Xki|Xki-1). 非插补条件最小二乘估计法与个案剔除法的差别在于非插补条件最小二乘法考虑非缺失数据间的缺失数据个数, 因为这里用的是非缺失数据间的条件期望, 而个案剔除法则不考虑非缺失数据间的缺失数据个数, 直接将非缺失数据放在一起视为完整数据. 若需要剔除的个案比例庞大, 则统计结果会有偏离, 此时需用均值插补法.该方法建立在完全随机缺失(指目标变量X的缺失概率与任何变量的取值均无关)的假设下, 用所有非缺失数据值的期望值对缺失单元进行填补.实际应用中这类缺失数据集很常见, 如对某地区环境质量的某个指标进行检测, 由于检测仪器的随机不工作, 可能会产生不完整的监测数据, 是一种完全随机缺失数据集, 适用于该方法进行缺失数据的填补.该方法不改变变量的均值估计, 是一种简便处理缺失数据的方法.本文在完全随机缺失机制下, 给出MGINAR(p)模型缺失数据的均值插补方法, 将其与完全数据统计推断方法相结合得到参数估计.算法步骤如下: 1) 观察数据的缺失情况, 将观测到的非缺失数据Xk1,Xk2,…,Xkm作为研究对象, 求数据期望; 2) 若所求期望为非整数值, 则将所求期望值四舍五入, 得到整数值, 并将其作为缺失数据的插补值; 3) 将插补后的数据作为完全数据X1,X2,…,Xn, 利用标准统计推断方法进行模型的参数估计. 如果缺失数据是非数值型的, 则可采用非缺失数据中取值次数最多的值插补缺失的数据, 但可能会产生有偏估计. 桥式插补法插补原理是通过比较估计值与真实观测值是否相等选取最终插补值[8].该插补方法适应于非缺失数据Xk1与Xk2之间存在j个缺失数据, 采用迭代方法, 生成预备候选插补值.在实际应用中, 这类数据集较常见, 如某医院收集特定疾病的患者进行医疗研究, 得到的数据一般会存在缺失的情况[9-12].缺失数据的桥式插补法算法步骤如下: 1) 基于MGINAR(p)模型, 从参数空间Θ中选取初值θ0; 4) 利用步骤2)插补所有缺失数据, 生成插补后新的完整数据集; 5) 进行参数估计, 如果估计达到事先约定的收敛标准则停止, 否则重复步骤2)~步骤4). 注1参数初值的选取方法, 利用剔除法将缺失数据剔除, 将非缺失数据视为等间隔完全数据, 得到的参数估计值作为参数初值. 注2桥插补法最终生成的数据如果与真实数据相差较大, 则需要多次操作, 才能达到预期效果. 注3在实际操作中, 由于模拟过程的收敛速度较慢, 因此要得到精确度高的估计结果较难. 下面通过数值模拟考察上述4种方法在处理缺失数据情况时一阶混合自回归模型的参数估计问题.考虑基于MGINAR(1)模型, 生成来自MGINAR(1)模型的100个随机样本, 对每组数据重复实现500次(舍弃前2 000次后), 记作X1,X2,…,X100, 其中参数(μ,α,p)真值分别取(2,0.3,0.4),(6,0.7,0.6).设缺失概率分别为5%,10%和15%. 1) 个案剔除法.将(n-m)个缺失数据剔除, 剔除后的样本视为完全样本, 可得到参数的条件最小二乘估计, 结果列于表1. 2) 非插补条件最小二乘估计法.基于MGINAR(1)模型, 可知 E(Xt+k|Xt)=αkXt+μ(1-αk)(k=1,2,…), Q(θ)的表达式为 3) 均值插补法.以均值插补法为例, 下面给出参数(μ,α,p)真值取(2,0.3,0.4)时完全随机样本的样本路径图.缺失概率分别为5%,10%和15%的样本路径和均值插补法插补后的样本路径, 分别如图1和图2所示.通过对均值四舍五入, 将缺失数据填补完整, 并得到参数的最小二乘估计, 模拟结果列于表1. 图1 完全样本路径和缺失样本路径Fig.1 Complete sample path and missing sample path 表1 不同缺失概率下参数估计的偏差和均方误差 Table 1 Bias and MSE of parameter estimation with different missing probabilities 条件参数估计个案剔除法非插补条件最小二乘估计法均值插补法桥式插补法A^μ(0.227 0, 0.095 9)(0.265 3, 0.149 4)(-0.220 8, 0.003 4)(0.343 6, 0.078 5)^α(0.096 7, 0.009 0)(-0.111 9, 0.027 8)(0.047 3, 0.001 2)(0.047 0, 0.006 4)^p(0.176 3, 0.062 6)(-0.035 3, 0.110 7)(-0.024 4, 0.005 1)(-0.209 7, 0.034 2)B^μ(0.790 0, 0.741 2)(-0.485 7, 0.569 3)(0.760 4, 0.003 2)(-0.432 9, 0.029 7)^α(0.012 0, 0.118 0)(-0.083 4, 0.228 1)(0.210 1, 0.020 6)(0.045 7, 0.011 2)^p(0.167 9, 0.067 4)(0.153 4, 0.031 2)(0.362 2, 0.001 9)(0.032 0, 0.003 3)C^μ(0.787 1, 0.296 2)(0.507 7, 0.291 5)(0.067 2, 0.001 5)(0.242 4, 0.061 4)^α(0.024 1, 0.013 9)(-0.044 6, 0.006 2)(0.010 4, 0.022 5)(0.043 0, 0.002 2)^p(-0.331 0, 0.038 0)(-0.173 4, 0.024 6)(0.001 7, 0.002 5)(0.021 5, 0.010 2)D^μ(-0.301 2, 0.806 2)(0.109 5, 0.022 1)(0.485 8, 0.004 2)(-0.090 3, 0.443 1)^α(0.072 2, 0.013 3)(-0.114 1, 0.007 9)(0.025 6, 0.009 8)(-0.007 0, 0.012 5)^p(-0.044 4, 0.020 2)(-0.005 4, 0.016 8)(0.019 1, 0.011 9)(0.154 6, 0.013 8)E^μ(-0.101 0, 0.055 2)(0.580 7, 0.286 6)(0.206 6, 0.055 2)(-0.148 9, 0.216 1)^α(-0.042 1, 0.005 9)(0.094 4, 0.011 4)(0.102 6, 0.002 9)(-0.066 0, 0.004 3)^p(-0.223 8, 0.028 2)(-0.086 4, 0.019 3)(0.021 1, 0.003 1)(-0.045 6, 0.013 1)F^μ(-0.786 4, 0.632 7)(-0.478 7, 0.034 4)(0.411 5, 0.013 5)(-0.245 3, 0.062 1)^α(0.049 9, 0.138 8)(0.234 2, 0.015 2)(0.106 5, 0.005 0)(0.095 5, 0.004 5)^p(0.135 7, 0.132 3)(0.300 9, 0.049 6)(0.221 4, 0.007 9)(0.108 3, 0.007 4) 注: A.(μ,α,p)=(2,0.3,0.4), 缺失概率为5%; B.(μ,α,p)=(6,0.7,0.6), 缺失概率为5%; C.(μ,α,p)=(2,0.3,0.4), 缺失概率为10%; D.(μ,α,p)=(6,0.7,0.6), 缺失概率为10%; E.(μ,α,p)=(2,0.3,0.4), 缺失概率为15%; F.(μ,α,p)=(6,0.7,0.6), 缺失概率为15%. 4) 桥式插补法.通过将非缺失数据集作为完全数据进行MGINAR(1)模型的参数估计, 得到参数(μ,α,p)的初值.若Xki与Xki+1为相邻两个非缺失数据,Xki与Xki+1之间有j个数据缺失, 则在参数初值和已知Xki的情况下, 通过模型的迭代可得到插补值.以缺失概率5%为例, 在模拟过程中可知X49,X54,X56,X93,X97为缺失的数据, 其中X53=2,X55=0, 通过参数初值和X53=2, 迭代出X54=2, 使得通过其迭代出的X55=0, 此时可将X54=2作为桥插补值.以此类推, 全部缺失值可插补完毕, 从而得出参数的最小二乘估计. 由表1可见, 当缺失概率较大时, 插补法效果优于非插补法.只有在缺失概率较小时, 非插补方法的偏差(Bias)和均方误差(MSE)与插补法差不多, 但随着缺失概率增大, 非插补方法的偏差和均方误差均有所增大.因此, 当缺失概率较大时, 建议不要直接删除缺失数据, 这样会导致样本量减少, 偏差增大, 估计效率也会降低.当缺失概率较小时, 均值插补法与桥插补法的偏差和均方误差没有太大差别.但当缺失概率增大时, 桥插补法的偏差和均方误差小于均值插补法, 也是因为桥插补法在插补要求上更精于均值插补法.当缺失概率较小时, 可使用简便的个案剔除法, 也可以使用均值四舍五入进行插补, 当缺失概率较大时, 建议使用桥插补法, 降低估计偏差.2 缺失数据处理方法
2.1 个案剔除法
2.2 非插补条件最小二乘估计法
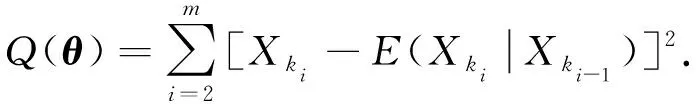
2.3 均值插补法
2.4 桥式插补法
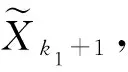
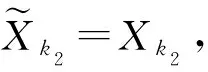
3 数值模拟