姐妹花齐上阵,英雄怎过美人关?
——基于指对数混合的函数不等式的一点思考
厦门大学附属实验中学 (363123) 吴赛瑛
指数函数y=ex与对数函数y=lnx堪称基本初等函数的一对迷人的姐妹花,以此为背景的函数导数压轴题一直是高考的重点、热点、难点,将两个函数在同一道题交汇考查,更是增加了试题难度,引得无数学子英雄竞折腰.本文旨在梳理基于指对数混合的函数导数不等式证明的解题策略,为高中师生提供一些解题方向,尽一丝绵薄之力.
一、花开堪折直须折,莫待无花空折枝
经全国中小学教材审定委员会2005年初审通过的人教A版高中数学教材第32页习题1.3B组第1题:利用函数单调性,证明下列不等式,并通过函数图象直观验证.以第3小题的不等式ex>1+x(x≠0)的证明为例,我们可以直接构造函数h(x)=ex-1-x,进而利用函数单调性可知h(x)>h(0)=0,从而得证.
例1 已知函数f(x)=lnx-ax2+bx,g(x)=xex-b,且f(x)在点(1,f(1))处的切线方程为y=2x-1.
(1)求a,b的值;
(2)求证:f(x)≤g(x).
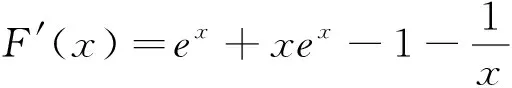
解答:(1)易得a=0,b=1.


点评:像这样可以直接构造函数求解,或是将不等式变形后可以直接构造函数求解的,算是相对简单的题,特别是适合高二的学生进行训练,而在高三总复习时,可能后续还有一问略难的.是否直接构造函数求解,显然取决于函数导数的特点.
二、能分人之兵,能按人之兵,则锱(铢)而有余
指对数混合的函数导数题之所以难,是因为对其直接构造函数,得到的导函数往往比较复杂(同时含有ex与lnx),二阶导更加复杂,让人无从下手,甚至根本无法判断导函数的正负及其零点的个数.如果能将lnx与ex分开,则可以有效的避免复杂导函数的出现.

(1)求y=f(x)在x=1处的切线方程;
(2)求证:f(x)>1.

解答:(1)易得y=e(x-1)+2.

因为p(x)和q(x)不同时取得最值,所以p(x)>q(x),即f(x)>1.
点评:为了让我们能尽快顺利用此法进行解题,就要求我们熟悉以下和指对数相关的经典函数:

三、好风凭借力,送我上青云
(一)借助试题前一步结论
为了让试题能有更好的区分度,让试题的结构浑然天成,在同一道题各个设问之间保持着一定的逻辑联系,同时也为了让考生面对较难的试题时有所解题方向(适当降低难度),命题者在前一步的设问常常是为做好下一步的铺垫,让考生能借助于前一步的结论来解决后续问题.从解题者的角度,必须注意观察题目的各问之间是否有联系,从而寻求解题突破口.
例3 已知函数f(x)=ex-1-x-ax2.
(1)当a=0时,求证:f(x)≥0;
(2)当x≥0时,若不等式f(x)≥0恒成立,求实数a的取值范围;
(3)若x>0,证明:(ex-1)ln(x+1)>x2.


(-1,+∞)上单调递增,当x>0时,有p(x)>p(0)=0,从而原不等式成立.
点评:面对试题无从下手之时,不妨看看前一问的结论是否对后续的解题有帮助.从本题可以看出,借助第(2)问的结论,较有效的降低了第(3)问的难度.若前一问含有参数,则常常将参数特殊化,而参数的特殊化取值测常取临界值.
(二)借助曲线的切线方程
曲线的切线具有很多的美妙性质,“以直代曲”[1]证明不等式更显示切线的魅力.有此问题需通过利用切线方程,将一个复杂的不等式,转化为两个相对简单的不等式,从而进行证明.

(1)求a,b的值;
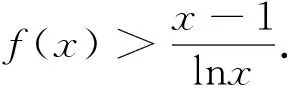

解答:(1)易得a=1,b=1;

点评:本例借助线切方程进行解题,确实有效的化解了直接构造函数的难度.但要找到一条满足条件的切线方程并不易,一般如果题设中给出了切线方程或是前一问求解的切线往往可以利用,或是尝试利用x=1处的切线方程.值得强调的是,这种解法利用的是充分不必要条件进行解题,所以若不能成功,要及时转换解题思路.
(三)借助常见不等式
不等式优美结论众多,而和指对数有关的不等式也是精彩纷呈,特别是以“lnx≤x-1,ex≥x+1,xlnx≥x-1”等经典不等式为代表.借助经典不等式,对指对数函数进行放缩的一个重要方向,也是有效降低不等式证明难度的一个策略.
例5 已知函数f(x)=xlnx.
(2)证明:f(x)+1 解题策略:观察(2)问不等式,发现(1)问的结论较难直接借用,且题中也未给出相关的切线方程可以借助.这时我们考虑对不等式的一边进行放缩,而那些经典不等式则为放缩提供了方向.由经典不等式lnx≤x-1,从而有xlnx≤x2-x,则要证原不等式只需证x2-x+1≤ex-x2(x>0);也可以考虑经典不等式ex≥x+1,则要证原不等式只需证f(x)+1 当x∈(0,x1)时,h′(x)>0,故h(x)在(0,x1)上单调递增,从而h(x)>h(0)=0①; 当x∈(x1,x2)时,h′(x)<0,故h(x)在(x1,x2)上单调递减,当x∈(x2,+∞)时,h′(x)>0,故h(x)在(x2,+∞)上单调递增. 都言教无定法,实则解题一样也无定法,如本文例5可以借助经典不等式lnx≤x-1进行证明,而借助ex≥x+1却未能成功,可以转化为证明“小边的最大值”小于“大边的最小值”,同时也要注意保证“小边有最大值”“大边有最小值”是前提.在解题时,只有根据题目题意,进行适当的尝试才能选择最优的解题方向. 要在高考考场上短时间内寻找适合的解法应对压轴题,对学生的要求是较高的,首先要有良好的考试心态,方能以自信的面对试题;其次,要掌握热点、重点题型相应的解题策略和思想方法,胸有成竹方能势如破竹;最后,要有较广的学科知识视野,比如本文例2点评提及的经典函数,例5提及的经典不等式,当然还有更多学科知识本文未能一一提及,见多识广,也能为解题提供重要的方向. 如果对各类试题、解题策略、解题方向都了然于胸,有良好的逻辑思维、发散思维、逆向思维,显然更有助于解题者能更好的、更快的选择适合方法.因此,在教育教学中,我们要有意识的培养学生的思维习惯.