基于近似梯度算法的Fisher线性判别分析问题的求解研究

梁露方，胡恩良

(云南师范大学 数学学院，云南 昆明 650500)

特征提取是模式识别中最基本的研究内容之一，它可以有效地缓解模式识别领域中经常出现的“维数灾难(curse of dimensionality)”问题，并对后续识别性能起着重要的作用[1].“维数灾难”问题，最早是由Richard E. Bellman[2]在思考问题的优化时所提出来的，而如何处理“维数灾难”成为了我们关心的话题.在高维的大数据中，并不是所有的信息都是重要信息，把信息处理后再利用会避免许多麻烦，例如：计算存储量的问题、信噪比的问题、鲁棒性的问题等，甚至还能避免影响后续的一些结果.

在众多的特征提取方法中，Fisher线性判别分析(Fisher linear discriminant analysis，FLDA)是一种经典的有监督的特征提取方法，它为多种线性判别分析奠定了基础.FLDA最早出现在1936年Fisher的经典论文[3]中，其基本思想是通过最大化Fisher准则，找到最优投影方向，使投影后的数据的类内距离尽可能小且类间距离尽可能大，并以此达到抽取分类信息和压缩特征空间维数的目的.目前，FLDA及其推广已广泛应用于市场定位、产品管理、人脸识别及机器学习等领域.

直到现在，我们对FLDA的拓展研究都没有停止.例如，2017年由Forough等[4]所写的文章就是对Fisher线性判别分析做出的进一步研究，其文章的核心是多类判别分析的迹比优化，而Li等[5]也在自己的文章中提出过相似的理论.Liu等[6]的文章提出通过最大化多目标函数的调和平均值来研究加权迹比，而为了进一步提高性能，就将L2，L1范数强加到目标函数上.此外，他们还提出了一个迭代算法来优化目标函数，Wei和Yang等[7-8]也提出过相似的理论.Liao等[9]提出的最坏判别特征选择也是基于FLDA的拓展研究.

设X=[x1,…,xn]∈Rd×n为c类样本矩阵，W=[w1,…wr]∈Rd×r为待求解的投影矩阵，Y=WTX为样本集X投影后的表示(即Y=[y1,…,yn]∈Rr×n，yi=WTxi).根据Fisher准则可知，求解投影矩阵W，等价于求解投影后的数据Y的类间散度与类内散度比值的最大化，即

(1)

其中，类间散度矩阵Sb、类内散度矩阵St的关系如下：

(2)

求解目标问题(1)等价于求解如下(3)的广义特征值问题：

SbW=λStW.

(3)

然而，问题(3)的求解时间复杂度至少为Ο(d3).为了提高求解效率，我们将引入近似梯度下降(PGD, proximal gradient descent)法[10-11]来求解FLDA问题.

1 近似梯度算法

1.1 混合凸目标函数的PGD算法

在凸优化问题中，对于目标函数是可微的时候，我们可以利用梯度下降法(GD，gradient descent)迭代求解出最优解，而对于目标函数是不可微的时候，则通过引入次梯度也可以迭代求解出最优解，但是比起梯度下降法，次梯度法的速度比较缓慢.因此，针对于一些整体不可微但却可以分解的混合目标函数来说，我们可以使用一种更快的算法—近似梯度法(PGD).

PGD是一种更广泛的梯度下降方法，该方法可用于求解一些目标函数是不可微的问题，其基本思想是使用临近算子得到目标函数的近似梯度.

考虑目标函数可以分解为如下形式的2个函数：

J(x)=f(x)+g(x).

(4)

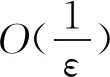
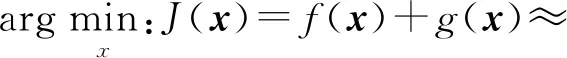
结合近似函数，我们可以定义一个迭代过程，叫做近似梯度下降(即PGD)，其过程如下：

(5)

PGD是一种传统算法的推广，易知：①当f(x)=0时，PGD退化为近似点算法；②当g(x)=0时，PGD退化为梯度下降法；③当g(x)=δX(x)是凸集的指示函数时，PGD退化为投影梯度下降法.

1.2 比值形式的PGD算法

对于如下的比值优化问题：

(6)

Radu等[12]在2016年提出过类似的近似梯度算法，其中g(x)≥0是凸函数，f(x)>0是凸函数或者凹函数.在f(x)是凸函数的情形下，分式PGD算法的迭代格式为：

(7)

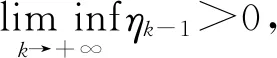
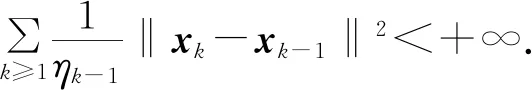
2 PGD算法求解FLDA问题

根据前文可知，笔者的目的是求出经过投影后的投影矩阵W中的各个投影方向，即W=[w1,w2,…,wr].由前面(1)式可知原目标函数可转化为：

(8)

(9)

2.1 子问题(9)的求解

记

(10)

对h(w)式关于w求导后令其为0，得：

2.2 WTW=I的正交约束处理

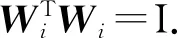
证明：利用数学归纳法进行证明

当i=1时，Wi=[w1]，结论显然成立；

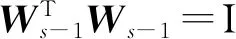
当i=s时，

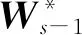
综上2.1和2.2所述，利用PGD求解FLDA问题(1)可整理为如下算法1：

算法1：利用PGD求解FLDA

输入：i=1，w0，Xi=X;输出：近似最优解W*.

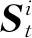
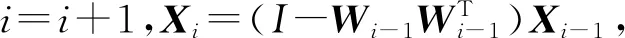
3 实验结果与分析

3.1 数据描述与实验设置

本节将选取12个数据集(具体信息如下表1)进行实验.其中数据集Chessboard、Glass、Heart、Iris、Protein、Sonar、Soybean和Spiral来自于UCI-9datasets[19]；数据集Diabetes、Air、Dnatest和Normal来自于UCI8.实验过程中对比的方法共4种，分别是：PCA[20]、FLDA_EigDcom[3]、FLDA_DC[21]和FLDA_PGD，其中：

PCA—即PCA降维方法；

FLDA_EigDcom—即利用广义特征分解求解FLDA；

FLDA_DC—即利用凸差(DC，Difference of Convex functions)优化方法求解FLDA；

FLDA_PGD—即利用PGD算法优化求解FLDA.

表1 实验的数据集及信息

3.2 降维效果对比

分别用PCA、FLDA_EigDcom、FLDA_DC和 FLDA_PGD 4种方法在训练集上得到降维矩阵，然后再对数据集进行降维.为了测试降维效果的好坏，我们利用最近邻分类，使用降维后的测试集上的平均分类精度作为比较标准，实验结果见表2.从表2可以看出，各个方法的平均分类精度都相差较小，但FLDA_PGD的平均分类精度最优，标准差也相对较小.

从表2可以看出，在多数情形下FLDA_PGD的平均分类精度为最优，标准差也相对较小.尽管PCA、FLDA_EigDcom、FLDA_DC和FLDA_PGD的差别较小，但多以FLDA_PGD的平均分类精度略高于另外3种方法，这说明了FLDA_PGD算法的有效性.

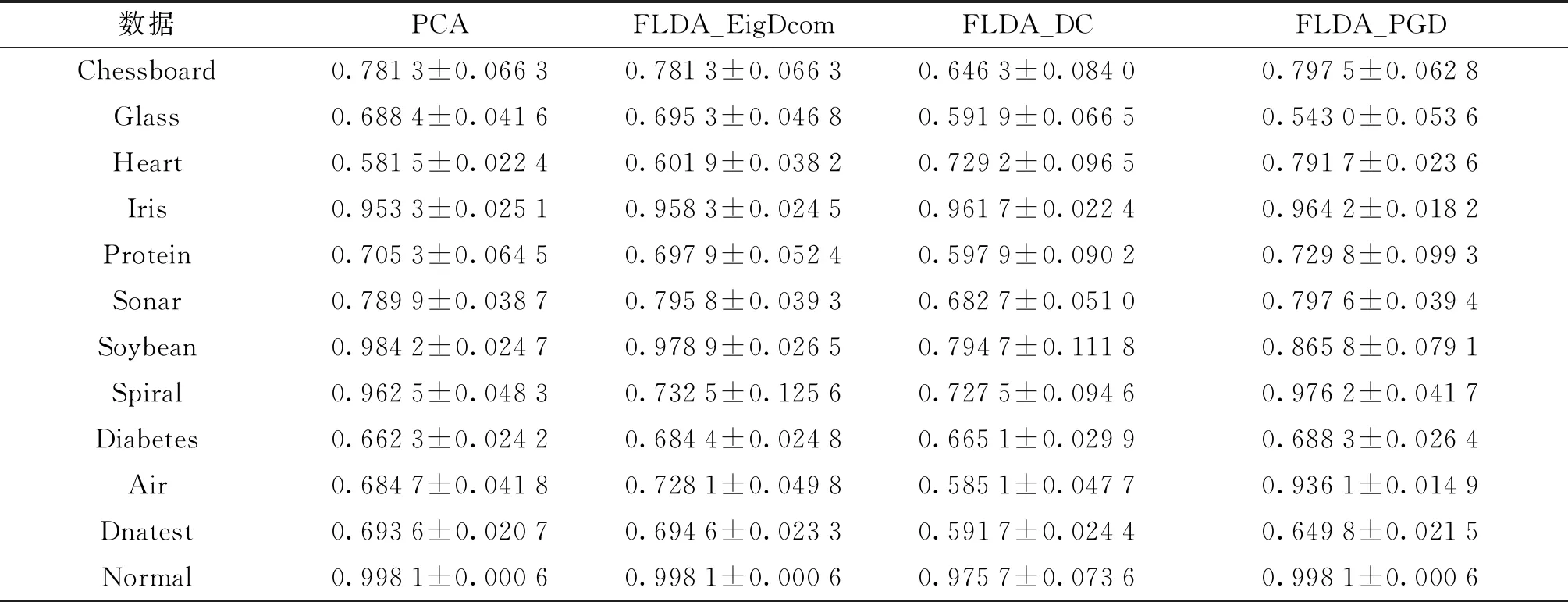
表2 4种算法在各数据集上的分类精度对比

注：表中数据为平均分类精度±标准差.

3.3 时间效率对比

从表3中可看出，FLDA_PGD算法的执行时间明显少于FLDA_EigDcom和FLDA_DC的执行时间，这表明该算法在求解FLDA问题时效率更高.

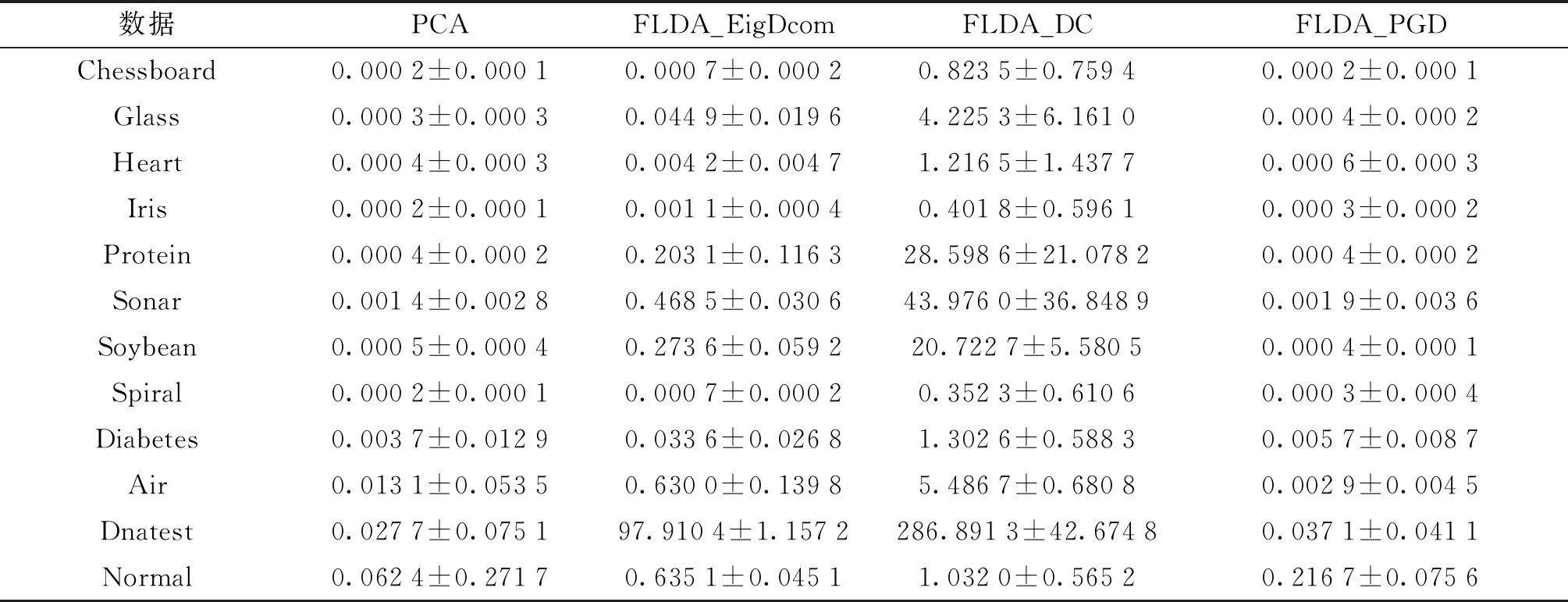
表3 4种算法在各数据集上的执行时间对比

注：表中时间为平均执行时间±标准差.

4 结语

为了更好地求解FLDA问题，引入近似梯度下降(PGD, proximal gradient descent)法来求解FLDA问题，并分析了该算法的收敛性.通过在多个数据上的实验表明，利用PGD方法进行实验大多比传统方法更好，后续的平均分类精度更高.同时，实验结果也表明，FLDA_PGD算法所耗时间较少，比一些传统方法(如FLDA_EigDcom和FLDA_DC)的效率更高.