圆弧曲线的二次有理Bézier表示方法

杨 艳，黄家珩

(吕梁学院 数学系，山西 离石 033001)

0 引言

圆弧曲线在CAGD中地位比较重要，一方面因为圆不能由Bézier曲线和B样条曲线精确表示，另一方面在旋转体的表示中，圆弧起到至关重要的作用，同时在圆弧的表示中，可以类似得到椭圆弧或椭球面的表示.

而自由曲线一般讨论Bézier曲线、B样条曲线、有理Bézier曲线和NURBS曲线.前两者的实质是多项式，可以简单得到圆的逼近，在[1]中详细叙述了3次Bézier曲线逼近圆的方法.B样条曲线逼近圆一般选用正8边形的控制顶点，选其中相邻4段轮换得到8条B样条曲线进行拼接.而有理Bézier曲线是NURBS曲线的特例，故研究用有理Bézier曲线精确表示圆.

以点pi(xi，yi)(i=0，1，…，n)为控制顶点，wi(i=0，1，…，n)为权重的一条n次有理Bézier曲线的表达式为：

(1)

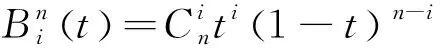
有理Bézier曲线有如下端点性质[2]：

P(0)=P0，P(1)=Pn，

即有理Bézier曲线的起点和终点过第一个和最后一个控制顶点，且在起点和终点的切线分别平行于最前两个和最后两个控制顶点的连线.这一性质用于判断二次有理Bézier曲线控制顶点的位置.

1 参数方程法

(2)

即圆的参数方程为二次有理多项式，故用二次有理Bézier曲线表示圆弧.特别地，当t∈[0，1]时，上述表达式表示的是第一象限的四分之一圆.

另一方面，由(1)式得，以P0(x0，y0)，P1(x1，y1)，P2(x2，y2)为控制顶点，w0，w1，w2为权重的一条2次有理Bézier曲线的参数形式为：

(3)

对比(2)式和(3)式，令分母相同，有

w0(1-t)2+2w1(1-t)t+w2t2=1+t2，

整理为，

(w0-2w1+w2)t2+(-2w0+2w1)t+w0=1+t2，

令左右两边对应项系数相等，可得下列方程组

解之得权重分别为：w0=1，w1=1，w2=2.

对比(2)式和(3)式，由分量x的分子相同，有

w0(1-t)2x0+2w1(1-t)tx1+w2t2x2=r(1-t2)

整理后，令左右两边对应项系数相等，可得下列方程组

解得x0=r，x1=r，x2=0.

同理，对比(2)式和(3)式，由分量y的分子相同，有

w0(1-t)2y0+2w1(1-t)ty1+w2t2y2=r·2t

整理后，令左右两边对应系数相等，列方程组，解得y0=0，y1=r，y2=r.

综合以上三个解，可得圆心为坐标原点，半径为r的第一象限四分之一圆的控制顶点坐标为p0(r，0)，p1(r，r)，p2(0，r)，对应权重分别为w0=1，w1=1，w2=2，如图1.根据Bézier曲线与B样条曲线的关系，可以将其表示为节点集为{0，0，0，1，1，1}的二次NURBS曲线.

对第一象限的四分之一圆进行对称，可得整圆，如图2，此处用四段有理二次Bézier曲线拼接生成整圆.由Bézier曲线与B样条曲线的关系，一方面可以将其理解为四条NURBS曲线拼接生成的结果.另一方面，应用B样条曲线的节点插值性，可以将整圆理解为节点集为

控制顶点为p0(r，0)，p1(r，r)，p2(0，r)，p3(-r，r)，p4(-r，0)，p5(-r，-r)，p6(0，-r)，p7(r，-r)和p8(r，0)，对应权重分别为w0=1，w1=1，w2=2，w3=1，w4=1，w5=1，w6=2，w7=1和w8=1的一条二次NURBS曲线.

图1 2次有理Bézier表示的四分之一圆图2 2次有理Bézier表示的整圆

2 几何方法

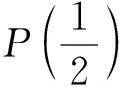
2.1 数学推导

如图3为圆心在坐标原点，半径为r，圆心角为θ的圆弧曲线P0*P2*，其中P0*位于x轴.为了写出曲线的2次有理Bézier表达式，需找出3个控制顶点P0，P1，P2和3个权重w0，w1，w2.根据其端点性质知，P0=P0*，P2=P2*，且P1为过P0，P2切线的交点，因此图中P0P1垂直于x轴.

图3 2次有理Bézier曲线表示任意大小圆心角的圆弧曲线

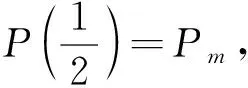
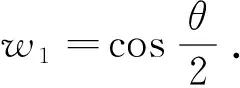
综上所述，圆心在坐标原点，半径为r，圆心角为θ的圆弧曲线P0*P2*，用2次有理Bézier曲线表示时，控制顶点为

P2(rcosθ，rsinθ)，权重为

w2=1.因此该圆弧2次有理Bézier表达式为

(4)

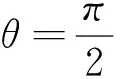
2.2 实践方法

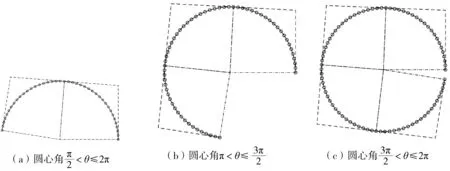
图4 拼接2次有理Bézier表示的任意大小圆心角的圆弧曲线

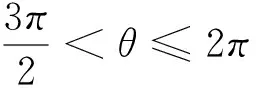
图4(b)、(c)与图3(b)、(c)对比，经分割后生成的圆弧曲线参数性和凸包性均较好.

3 小结

圆弧曲线的2次有理Bézier曲线和2次NURBS曲线是CAGD中常用的方法，研究比较透彻，但是用圆的参数方程直接有理化的结果比较容易理解.同时一般的做法都是经过分割成锐角进行的，但是在实验过程中发现不分割的结果也是精确的，为了弄清楚这个问题，做了详细的实验，发现确如文献[5]所述，分割后能够克服凸包性和参数化差的缺陷.文中重点从图形角度直观凸包性和参数化.