具有分布时滞的二阶广义中立型微分方程解的振动性

雷凤生

(吕梁学院 数学系，山西 离石 033001)

文章考虑如下带有分布时滞的二阶广义中立型微分方程

(1)

其中z(t)=x(t)+p(t)x(τ(t))，t≥t0.

在本文中，总假定下列三个条件成立.

(H1)a，b，α>0，β>0都是常数，此外，b>a；p∈C([t0，)，[0，1))；r∈C1([t0，)，[0，))，当t≥t0时r′(t)≥0；

(H2)τ∈C1([t0，)，R)，q∈C([t0，)×[a，b]，[0，))，g∈C([t0，)×[a，b]，(0，))，q(t，ξ)≠0；对任意的ξ∈[a，b]有；；对任意的ξ∈[a，b]，t≥t0有g(t，ξ)≤t，gt(t，ξ)>0，gξ(t，ξ)≥0；

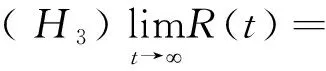
1 引理

引理1[1]设θ，A，B都为常数；θ>0，B>0，A≥0.则对任意的u>0有

(2)

2 结论

定理1假设存在函数ρ∈C1([t0，)，(0，))(其中ρ′(t)≥0)和任意的m∈(0，1]满足

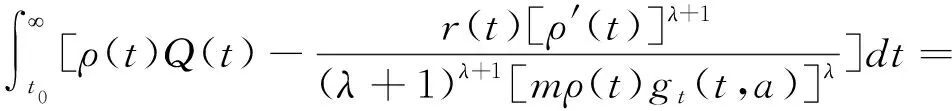
(3)

证明 假设方程(1)有一个非振动的解x(t).不失一般性，设x(t)是方程(1)的一个最终正解.所以存在T0≥t0使得当t≥T0时有x(t)>0.如果x(t)是最终负解，其证明过程是类似的[2].

由(H2)可知存在T1≥T0，使得当t≥T1时，有τ(t)≥T0以及g(t，ξ)≥T0.再结合(H1)，可得当t≥T1时有

x(g(t，ξ))>0，x(τ(t))>0，z(t)≥x(t)>0，[r(t)|z′(t)|α-1z′(t)]′≤0.

(4)

由(4)易知z′(t)是最终非负的或最终负的.假设z′(t)是最终负的，由文献[ 1]中定理1的证明过程可得一个矛盾.因此z′(t)是最终非负的.即存在T3≥T2，使得当t≥T3时，有z′(t)≥0以及z′(g(t，ξ))≥0.此时，方程(1)可变形为

(5)

由(4)可得，当t≥T3时，有

[r(t)(z′(t))α]′=r′(t)(z′(t))α+r(t)α(z′(t))α-1z″(t)≤0.

由(H1)和(4)，可得

z″(t)≤0，t≥T3.

(6)

故存在T4≥T3，使得z′(t)>0，t≥T4；或者z′(t)≡0，t≥T4[3].

事实上，如果当t≥T4有z′(t)≡0，可得当t≥T4时，有q(t，ξ)≡0，与(H2)相矛盾.故

z′(t)>0，t≥T4.

由于z(t)≥x(t)，可得当t≥T4时，有

x(t)=z(t)-p(t)x(τ(t))≥z(t)-p(t)z(τ(t))≥[1-p(t)]z(t).

故

xβ(t)≥[1-p(t)]βzβ(t)，t≥T4.

由(H1)和(H2)，可知存在T5≥T4，使得

xβ(g(t，ξ))≥[1-p(g(t，ξ))]βzβ(g(t，ξ))，t≥T5，ξ∈[a，b].

由(H2)可知，当t≥T5时，有

(7)

由(5)和(7)可得，当t≥T5时，有

因此有

(8)

令

(9)

另有

(10)

和

(11)

当t≥T5时，有

(12)

当α=β时，由(H2)、(6)、(8)、(10)和(12)可得当t≥T5时，有

(13)

当α<β时，由(10)和(12)可得当t≥T5时，有

(14)

由于z′(t)>0，t≥T4.故由(H2)可得

(15)

显然m1>0.由(6)、(8)、(14)和(15)可得，当t≥T5.时，有

(16)

当α>β时，由(11)和(12)可得，当t≥T5时，有

(17)

由(6)可得

(18)

显然m2>0.由(6)、(8)、(17)和(18)可得，当t≥T5.时，有

(19)

由(13)、(16)、(19)和引理1可知，存在m∈(0，1]，使得

(20)

对(20)左右两端从T5到t积分，可得

(21)

令t→，由(3)可得.与(9)矛盾.因此，方程(1)的解是振动的，得证[4].

注：在定理1当中令ρ(t)=1，可以得到下列结果.

推论1 如果

则方程(1)的解是振动的.