单自由度振动系统频率求解方法探讨
——以34届全国中学生物理竞赛试题为例
鲁斌 向豪 冯子江
(浙江省余姚中学 浙江 宁波 315400)
2017年由重庆大学举办的第34届全国中学生物理竞赛中,预赛、复赛、决赛试题都考察了振动系统的频率求解问题.此类问题不仅是高中竞赛考查的重点,也是大学物理课程教学的重点和难点.
1 试题概述和初步分析
【初试试题】如图1所示,两劲度系数均为k的同样的轻弹性绳的上端固定在一水平面上,下端悬挂一质量为m的小物块.平衡时,轻弹性绳与水平面的夹角为α0,弹性绳长度为l0.现将小物块向下拉一段微小的距离后从静止释放,求物块做微小振动的频率.
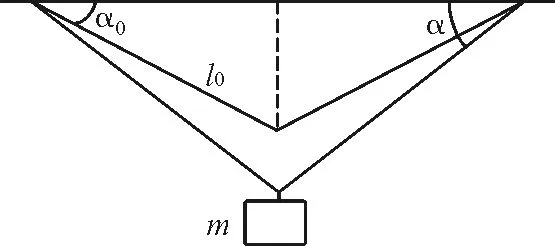
图1 初试试题图
由于物体只能在竖直方向振动,故此题考查单自由度振动系统的频率求解问题.复赛与决赛试题同样考察单自由度振动.此类问题在大学物理的练习和试题中比较常见,诸多教师对其也做过相关的探讨[1].
我们以此题为例,总结此类问题的常用解法,并谈谈几种解法的区别和联系.
2 一般解法讨论
振动频率求解方法,一般是通过受力分析、能量微分等方法,得到简谐振动的微分方程
其中y为物体离开平衡位置的微小距离.由式中的m,k即可得到圆频率.
2.1 受力分析的一般解法
对于受力分析法,我们认为α和y均在有限范围内变化,分析得到某一位置的回复力F关于离开平衡位置位移y的表达式,然后考虑y为小量,进行合理近似,保留一阶小量.只要证明F为线性回复力即可.
设原长为L,现在长度为l,与水平面所成的夹角为α,如图2所示,则此时,物体受力
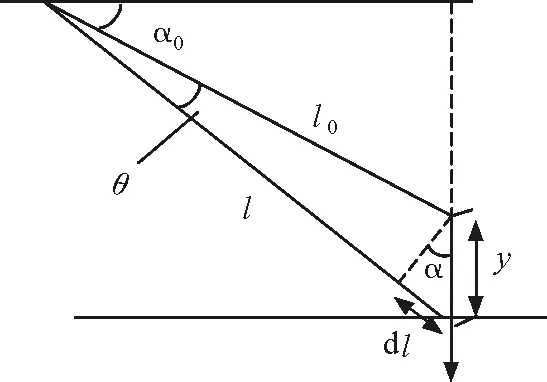
图2 各物理量之间的关系
F=mg-2k(l-L)sinα
(1)
在平衡位置满足
mg=2k(l0-L)sinα0
(2)
得到原长
(3)
根据几何关系,现有长度l可以表示为
(4)
将式(2)~(4)代入式(1),有
mg-2k(y+l0sinα0)-
(5)
此为合力关于位移的关系.其中
(6)
保留y的一阶小量,式(6)为
(7)
将式(7)代入式(5),得到
F=mg-2k(y+l0sinα0)-
化简得
(8)
根据牛顿第二定律,有
(9)
由简谐振动微分方程得
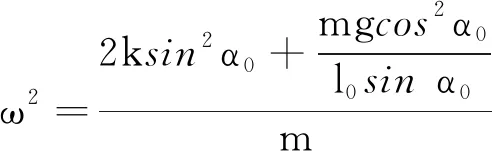
(10)
系统微小振动的圆频率为
物块微小振动的频率为
受力分析法的关键在于找到微小位移所对应的力的变化,但如果涉及的物理量较多,很容易出现小量近似舍去过多的情况.此种方法适合较明确、直接的振动系统.
2.2 能量的一般解法
能量求解的基础是保守系统的机械能守恒.振动系统中,先列出机械能守恒的表达式,接着将其各个变量对时间求导,求导结果为零.经过化简,便可得到简谐振动的微分方程.
振动系统的机械能由重力势能、弹性势能和动能组成.以平衡位置为零势能面,向下拉以微小位移y后,有
(11)
式(11)中,l是y的函数,对其进行泰勒展开.由于能量解法需要对时间求导一次,y的次方会低一阶,而我们的目标是得到线性回复力,故泰勒展开时涉及y,y2的项均应保留,故应展开到第三项.即
(12)
其中o(y2)表示y2的高阶无穷小.略去o(y2)可得
(13)
(14)
将式(14)代入式(11),有
(15)
即可求解.
3 不同角度的探讨
受力分析和能量微分是解决振动系统的常用方法.接下来,我们从不同角度讨论单自由度的振动问题.
3.1 角动量定理
将此振动系统看做转动系统,便可运用转动定律求解.在平衡位置时,弹簧与水平方向的夹角为α0,振动的某一时刻,夹角为α.角度的变化为θ(如图2所示)
θ=α-α0
(16)
由几何关系得
(17)
如图3所示,以绳子的悬挂点A为参考点,其受到的力矩有自身的重力矩和右侧弹簧的拉力矩.取垂直纸面向里为正.重力矩为
MG=mgl0cosα0
由于左侧弹力通过A点,不产生力矩,右侧弹力方向沿右侧弹簧,与左侧弹簧所成的角度为2α,如图3所示.
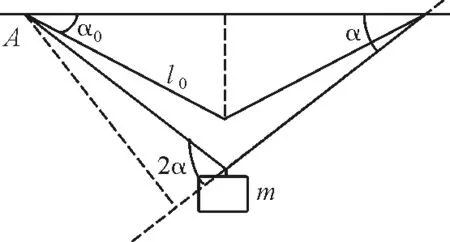
图3 角度的表示
则物体所受到的弹力矩为
MF=-κ(l-L)lsin 2α
根据小物块绕A点转动,由角动量定理
mgl0cosα0-k(l-L)lsin 2α=
(18)
其中绕A点的转动惯量为
IA=ml2
(19)
(20)
将式(17)、(19)代入式(20),有
为θ的高阶小量可以忽略,故
(21)
将式(3)、(19)、(21)代入式(18),等式两边同除以l2,有
(22)
进行求解前,先给出几个函数的近似式
cos2(α0+θ)=(cosα0cosθ-sinα0sinθ)2=
cos2α0cos2θ+sin2α0sin2θ-2cosα0cosθsinα0sinθ=
cos2α0-2cosα0sinα0θsin (2α0+2θ)=
sin 2α0cos 2θ+cos 2α0sin 2θ≈
sin 2α0+2θcos 2α0cos (α0+θ)=
cosα0cosθ-sinα0sinθ≈
cosα0-θsinα0sin (α0+θ)=
sinα0cosθ-cosα0sinθ≈sinα0-θcosα0
第一项
(23)
第二项
-ksin (2α0+2θ)≈-k(sin 2α0+2θcos 2α0)
(24)
第三项
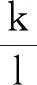
k(sin 2α0-2θsin2α0+2θcos 2α0)
(25)
第四项
(26)
将式(23)~(26)代入式(21),化简即可得到
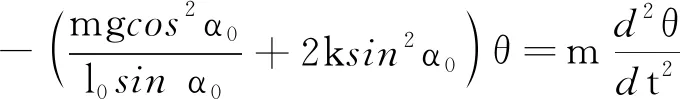
(27)
此法求解的关键在于选定参考点后,列出物体所受精确的力矩表达式,配合角动量定理求解即可.在求解过程中也应注意,代入的I应是针对环绕点的转动惯量,并且I为变量,代入的M也应是针对环绕点的合力矩.
3.2 将振动系统分解
将物块的上下振动看做不同振动方向的合振动,且各个振动方向分振动的频率必然一致,故只要得到沿着一侧的牛顿二定律即可求解.
将重力沿一侧分解,并计入弹力,得到动力学方程
-k(l-L)+mgsinα+k(l-L)cos 2α=
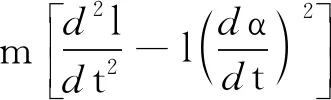
(28)
由于
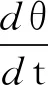
则式(28)为
(29)
第一项
mgsinα=mg(sinα0-θcosα0)
(30)
第二项
k(l-L)(cos 2α-1)=
(sinα0-θcosα0)2=
(sin2α0-2θsinα0cosα0)=
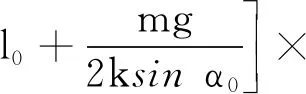
-2kl0tanα0sin2α0-mg(sinα0-2θcosα0)
(31)
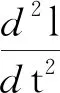
(32)
将式(30)~(32)代入式(29)可得
-(2kl0tanα0sin2α0+mgcosα0)θ=
化简整理后即可得到式(27).此解法益处在于小量只用展开到一阶,计算较为简单.
4 结束语
在振动问题的求解中,运用受力分析、能量微元是解决系统振动频率问题的一般方法,最终都要证明回复力为线性回复力.在受力分析时,应给出最精确的受力表达式,然后逐步代入,并保留一阶小量,进而求解.在能量求解中,应给出在保守场中的能量守恒表达式,求导后逐步代入参数求解.从另外的角度,将直线运动系统看做转动系统,借用角动量定理求解;根据运动的合成规律将振动系统分解等方法,也都能很好地解决此类问题.解决振动问题的分析方法多种多样,没有优劣之分,不同的问题可运用不同的方法解决.

