时间分数阶次扩散方程的多层扩充算法
陈 剑, 曾泰山
(1. 佛山科学技术学院数学与大数据学院, 佛山 528000; 2. 华南师范大学数学科学学院, 广州 510631)
分数阶导数具有非局部性,相比整数阶导数,它能更精确地描述现实世界中具有记忆和遗传性质的问题. 因此,分数阶微分方程已被广泛应用于众多领域,如半导体物理、弹性力学、生物学异速生长、金融学期权定价、信号处理和分形理论等[1-2]. 但分数阶导数的非局部性使得这类方程难以获得解析解,或者解析解需要用特殊函数来表达,这不利于实际应用. 所以,研究其数值解显得尤为重要.
本文研究如下时间分数阶次扩散方程的初边值问题:
(1)

这里Γ(·)表示Gamma函数.
时间分数阶次扩散方程是一类重要的数学模型,常被用于描述运输中的反常扩散行为,能很好地刻画长时记忆的流通过程. 已有很多学者研究了有关时间分数阶次扩散方程的数值方法[3-12],如:给出了一种隐式差分格式,讨论了格式的收敛阶,证明了该格式无条件稳定[3];研究了二维问题的一种高阶紧致差分格式[5];给出了一种有限元方法,并证明了所得全离散格式具有超收敛性[4];给出了一种时间方向具有二阶收敛阶的有限元计算格式,证明了该格式无条件稳定且空间方向具有最优收敛阶[6];利用经典有限元方法讨论了时间分数阶对流扩散方程和电报方程的数值解[7-8];给出了一种最小二乘谱方法[9];运用时空谱方法讨论了方程(1)的数值解,并获得了先验误差估计[10]. 但上述方法并未涉及全离散所得线性方程组的快速求解问题. 事实上,对于大尺度、高精度的实际问题而言,全离散格式将导出一个大规模的线性方程组,而求解该方程组需要消耗巨大的计算量.
为了高效求解全离散所得线性方程组,本文研究了方程(1)的一种多尺度快速方法. 首先,基于时间方向采用L1逼近和空间方向采用多尺度Galerkin逼近建立全离散格式,给出了全离散格式的误差估计;然后,利用矩阵分裂策略设计快速求解该全离散格式的多层扩充算法,并证明了该算法具有最优收敛阶.
1 预备知识
本节介绍一些相关记号和引理,以方便后文引用. 没有特别说明,后文中出现的字母c表示与时间和空间步长无关的常数,不同的位置可能表示不一样的常数.
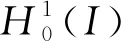


Xn=Xn-1⊕⊥Wn=X0⊕⊥W1⊕⊥W2⊕⊥…⊕⊥Wn,
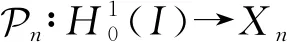
〈u-nu,v〉1=(∂x(u-nu),∂xv)=0(uXn).
引理1[5]设m,r,r≥1是正整数,u如果1≤m≤r+1,则
‖u-nu‖p≤c2-(m-p)n‖u‖m(p=0,1).
2 L1-多尺度Galerkin全离散格式
本节给出时间分数阶次扩散方程(1)的L1-多尺度Galerkin全离散格式,并推导其误差估计.
其中,aj=(j+1)1-α-j1-α(j≥0). 根据文献[2],如果uC2([0,T];L2(I)),则用逼近分数阶导数的截断误差为:

(2)

(3)
其中,fk=f(x,tk).
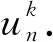

(4)



(5)
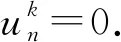
接下来论证误差估计. 由方程(1)可知,真解uk满足方程
(6)

(7)
由于1=a0>a1>a2>…>an>0,则由Cauchy-Schwarz不等式、三角不等式及引理2,有

再注意到式(7)左端第二项非负,则有
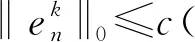
从而由三角不等式及引理2,有

证毕.

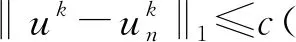
3 求解全离散格式的多层扩充算法
基底的多尺度特性使得全离散格式(3)对应的线性方程组的系数矩阵具有高低频层次结构,因此,本文利用多层扩充法进行高效求解. 为了方便叙述,先将全离散格式改写成:

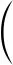
(8)
(9)
其中,En=[(w′ij,w′i′j′):(i,j),(i′,j′)Jn],Kn=[[(wij,]wi′j′):(i,j),(i′,j′)由基底的正交性可知En是单位矩阵.
为使用多层扩充算法,先将Kn进行分块. 对m0,p,p′+,记
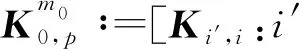
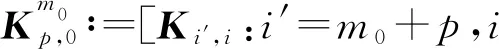
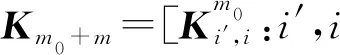
其中
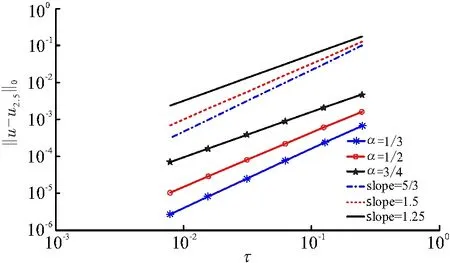
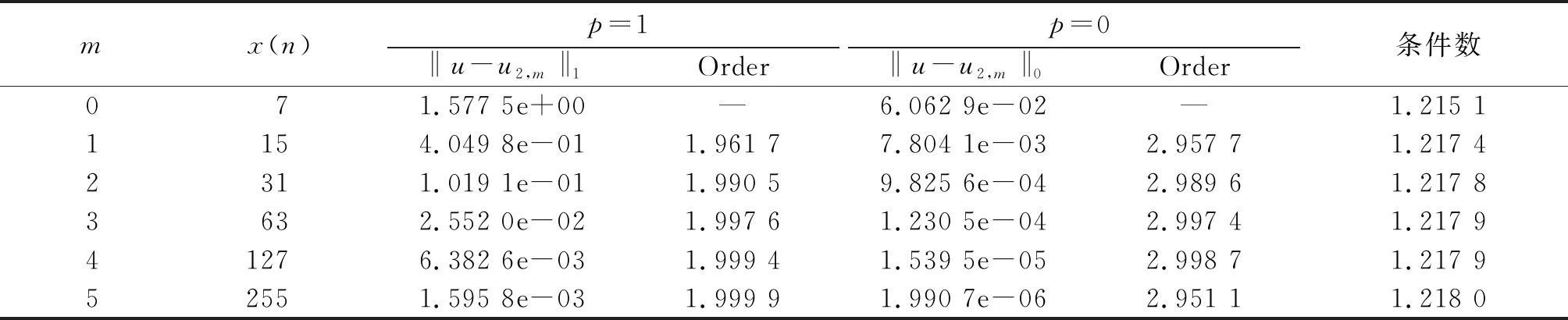
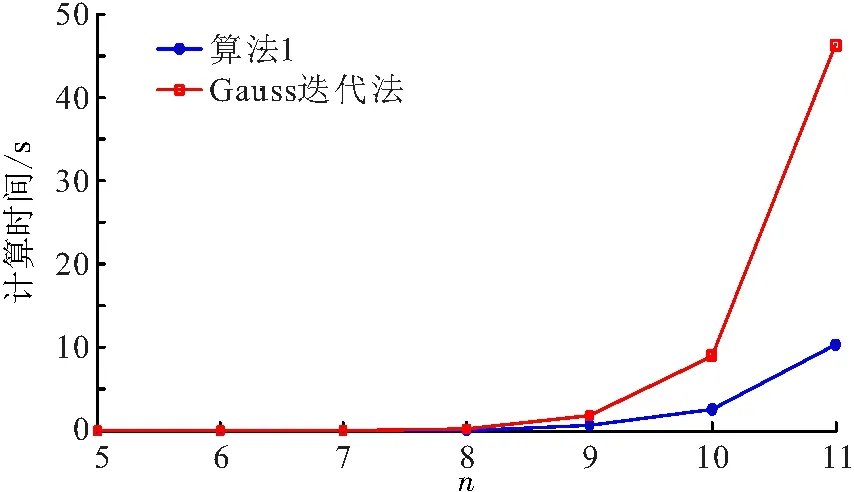
记m0和m是2个固定的正整数,m0< 算法1求解线性方程组(8)的多层扩充算法 本节以数值算例来验证本文的理论估计和算法1的计算效果. 考虑方程(1),其中 u0(x)=2sin(2πx), 其真解u=(tα+2+t+2)sin(2πx). 为验证算法1的时间收敛阶,选取二次多尺度正交基(基底具体构造可参看文献[14]),并在多层扩充求解时取(m0,m)=(2,5),时间步长分别取为1/4、1/8、1/16、1/32、1/64、1/128,对不同的α进行测试. 由所得结果(图1)可以看到:数值结果与理论的时间收敛阶2-α相吻合. 图1 u2,5(x,t)在t=1时刻的时间收敛阶 在空间方向,分别取线性基底和二次基底进行数值计算,用算法1时,初始层m0分别取为4和2,m表示扩充的层数,x(n)表示相应逼近子空间的维数,n=m0+m. 收敛阶为: 这里p可取1和0,分别对应H1和L2范数. 对于线性和二次基底,其H1范数的理论收敛阶分别为1和2;其L2范数的理论收敛阶分别为2和3. 由表1和表2可以看到:算法1所得的数值结果与理论收敛阶非常吻合. 利用Matlab中的Cond命令,计算了系数矩阵En+Kn的条件数,从表1和表2可知条件数一致有界. 表1 线性基底的数值结果Table 1 The numerical results for linear basis 表 2 二次基底的数值结果Table 2 The numerical results for quadratic basis 在计算效率方面,对比算法1与Gauss迭代法在线性基底下的数值结果. 由对比结果(图2)可知:算法1具有更高的效率,而且问题规模越大,其计算优势越明显. 图2 算法1与Gauss迭代法的计算时间对比 Figure 2 The comparison of computational time between algorithm 1 and the Gauss iteration method
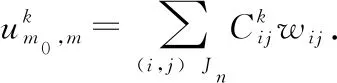
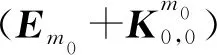
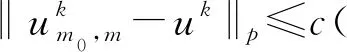
4 数值算例

5 结束语


