电能质量信号压缩采样匹配跟踪算法研究
刘传洋,孙 佐,刘景景*,方曙东,李春国,宋 康
(1.池州学院 机电工程学院,安徽 池州 247000;2.东南大学 电子科学与工程学院,江苏 南京 210096;3.青岛大学 电子信息学院,山东 青岛 266071)
电气信息化的发展及电网规模的不断扩大,提高了电力系统运行的自动化、信息化水平,但是大量的电能质量数据存储和传输给电力系统运行造成极大的负担[1]。电力设备中非线性负载和冲击负载的大量接入,电力设备电压和电流波形产生严重畸变,造成电能质量污染,使得电能质量识别在电力系统中发挥着重要作用[2-3]。CS压缩感知(Compressed Sensing)理论能够以远小于香浓理论采样标准对信号进行随机采样,在变换域对信号进行稀疏分解,利用与稀疏基不相关的观测矩阵将高维稀疏信号降维到低维空间,通过求解优化问题后重建原始信号[4]。
CS理论以重构精度高的特点引起了很多学者的关注[5]。信号重构方法有基于最小l1范数的凸松弛算法和基于最小l0范数的匹配追踪类算法。凸松弛算法通常被用来解决凸优化问题,具有较好的重构性能,但是对噪声敏感。匹配追踪类算法包含稀疏度已知和稀疏度自适应两大类。稀疏度已知算法[6-8]是在匹配追踪算法的基础上改进的一些算法,CoSaMP压缩采样匹配追踪(Compressive Sampling Matching Pursuit)算法应用最为广泛[9]。CoSaMP算法运算时间短、重构精度高且具有很好的鲁棒性,能够在噪声及干扰环境下较好地恢复压缩信号,但是需要提前预知稀疏度,在稀疏度未知的情况下,该算法的使用将受到限制[10]。稀疏度自适应算法采用稀疏度自适应匹配追踪(Sparsity Adaptive Matching Pursuit,SAMP)[11-12],该算法在信号稀疏度未知条件下恢复压缩信号,但是迭代调整稀疏度运行时间较长,重构精度与固定步长设定有关,如果设定固定步长越大,迭代次数就越少,造成原始信号的重构精度偏低;如果设定固定步长越小,相应的迭代次数越多,重构耗时就越长。
电能质量信号的稀疏度通常是未知的,为了使电能质量信号达到稀疏度自适应和重构效果好的目的,综合CoSaMP算法和SAMP算法的优点,研究提出一种稀疏度自适应的压缩采样匹配追踪算法(Sparsity Adaptive of Compressive Sampling Matching Pursuit,CoSaSAMP),引入稀疏度估计对信号的初始稀疏度进行迭代估计,利用递归和残差变化动态调整稀疏度逼近信号的真实稀疏度,通过最小二乘法重构原始信号最优估值。
1 压缩感知
1.1 压缩感知理论
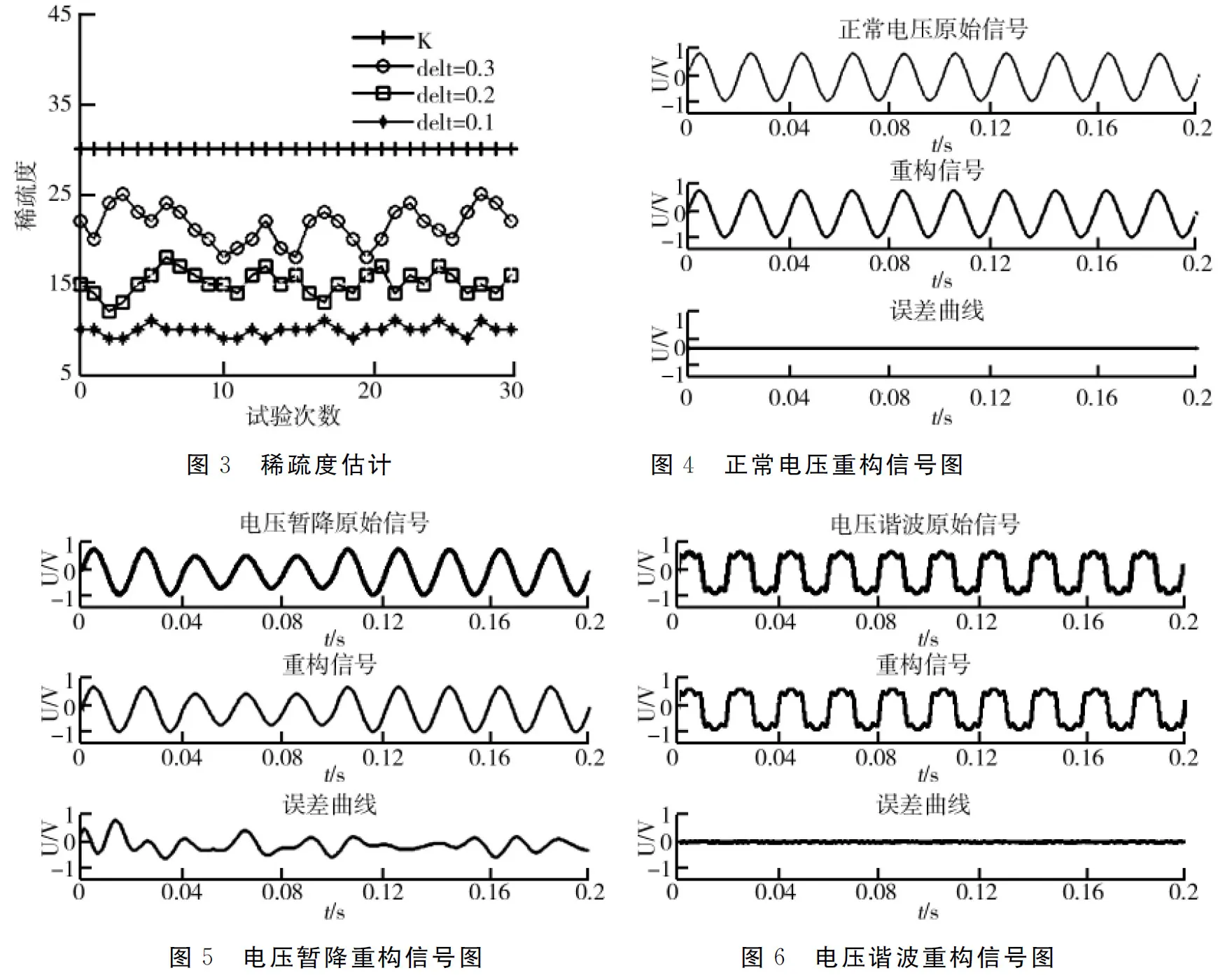
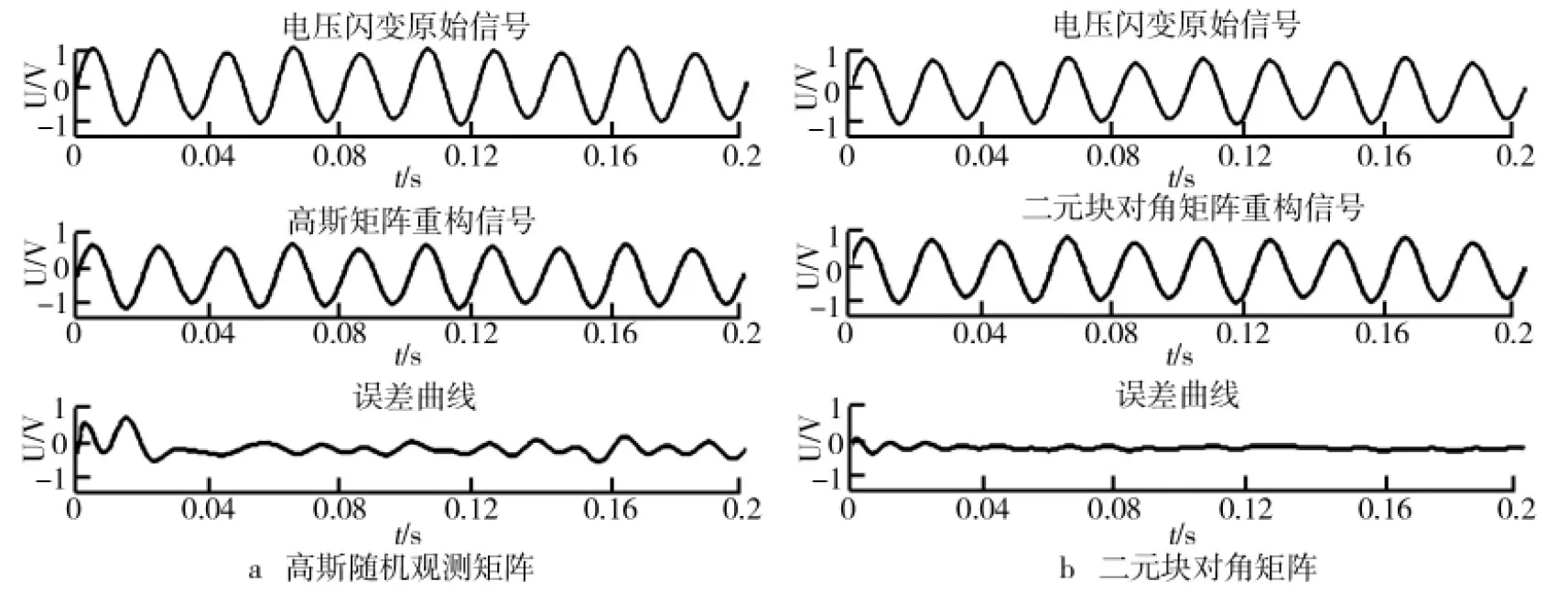
CS理论是Donoho等在2006年引入信号处理中的一种压缩技术,在电能质量识别中已经被广泛使用。文献[13]对随机降维映射稀疏表示的电能质量扰动多分类进行研究,实现电能质量扰动的准确识别;文献[14]基于压缩感知理论提出了暂态和短时电能质量扰动信号的压缩采样与重构方法;文献[15]采用一组固定正交基对电能质量扰动信号稀疏分解,对于未知复杂信号难以在变换域上足够稀疏,CS理论依赖于信号的稀疏性对其进行压缩重构。长度为N的信号x∈R具有K稀疏表示,在N维变换基Ψ∈RN下得到α∈R(x=Ψα),其中α有K个非零元素,(N-K)个接近于零。CS理论通过矩阵ΦM×N进行压缩采样(K y=Φx=ΦΨα=Aα, (1) 一个N维度信号有K个非零值时,此信号是一个K稀疏可压缩信号,在对信号进行变换的基称为稀疏基,稀疏基Ψ的选择尽可能降低稀疏度K。压缩感知中稀疏基通常采用正交变换基或基于学习算法构成的稀疏字典[17-18]。傅里叶变换基作为一种常用的正交基,在频域具有方便的稀疏性和简易性,研究中稀疏基采用离散傅里叶变换基,DFT正变换定义为: (2) 测量矩阵在CS理论中的作用是使压缩采样值能较好地保留原始信号的信息。高斯随机矩阵通用性强,常选用高斯矩阵作为测量矩阵。不论选用哪一种稀疏基Ψ,高斯矩阵Φ都要使矩阵A=ΨΦ满足RIP条件。由于RIP准则过于复杂,文献[19]计算测量矩阵Φ和稀疏基矩阵Ψ的乘积作为相关性系数,通过相关性系数大小判定测量矩阵的性能优劣。两个矩阵相干性表达式如下: (3) 由于匹配追踪类算法的测量矩阵大多采用高斯随机矩阵,二元块对角矩阵、高斯随机矩阵在相同离散傅里叶变换基下的相干性对比曲线如图2所示,其中N的维度为600。从图2中看出,M的维度从50递增到400,二元块对角矩阵与离散傅里叶变换基的相干性从4降低到2,而高斯随机矩阵与离散傅里叶变换基的相关性在4和5之间。因此,所设计的二元块对角矩阵相比于高斯随机矩阵具有更优的性能。 综合CoSaMP算法抗干扰能力强且重构精度高和SAMP算法稀疏度自适应估计的优点,利用递归思想提出了CoSaSAMP算法。该算法引入稀疏度估计方法提前对信号的初始稀疏度进行迭代估计,利用递归算法通过残差变化动态调整稀疏度逼近信号的真实稀疏度,通过最小二乘法重构出原始电能质量信号最优估值。 ΦB=[1…1]︷m[1…1]︷m⋱[1…1]︷m图1 二元块对角矩阵图2 相干性对比曲线 CoSaSAMP算法步骤如下: 输入:观测向量y,传感矩阵Φ; 步骤2:计算u={ut|ut=|〈rt-1,φj〉|,j=1,2,…,N},选取u中K0个最大值,映射在传感矩阵Φ相应列构成索引集合Λ0。 步骤4:计算委托代理v=ΦTrk-1,选取v中2KS个最大值,将2KS个最大值在Φ中映射对应的列序号加入索引集Ω。 步骤8:如果‖rk‖2<‖rk-1‖2,k=k+1,KS=KS+step,返回步骤4继续迭代;如果‖rk‖2≥‖rk-1‖2或k≥L,停止迭代,K′=KS,进入步骤9。 为了验证提出的CoSaSAMP算法在电能质量扰动处理中的可行性,研究以MATLAB 2014a作为信号处理平台,进行电压暂降、电压谐波、电压闪变等多种电能质量信号重构处理,并对得到的结果进行分析。 通过仿真验证CoSaSAMP算法稀疏度自适应估计,以电压闪变为例,电压闪变信号的稀疏度设为30,通过30次试验,自适应调节结果如图3所示。从图3中可以看出,CoSaSAMP算法稀疏度估计曲线与ζk的选取有关,ζk设置越小,稀疏度估计越大。为了减少算法迭代次数,可以选择适当的数值设定为稀疏度初始值。 使用CoSaSAMP算法对电能质量扰动信号进行重构,观测矩阵采用二元块对角矩阵,稀疏基采用傅里叶变换基,电压基波频率为50 Hz,压缩采样频率为6 400 Hz,电能质量信号长度N取2 048,观测数M取256。正常电压原始信号重构曲线如图4所示,电压暂降和电压谐波原始信号重构曲线如图5、图6所示。从图4、图5、图6中可以看出,CoSaSAMP算法可以精确重构出电能质量扰动信号。在稀疏基为傅里叶变换基,观测矩阵分别是高斯随机矩阵、二元块对角矩阵的条件下,电压闪变信号的重构图如图7所示。通过对比得出,图7b比图7a的重构误差小、重构精度高。由于二元块对角矩阵与傅里叶变换矩阵的相干性小于高斯随机矩阵与傅里叶变换矩阵,二元块对角矩阵更容易满足RIP准则,因此观测矩阵为二元块对角矩阵要比高斯随机矩阵具有更好的重构效果。 图7 基于高斯随机观测矩、二元块对角矩阵的电压闪变重构信号图 为了分析CoSaSAMP算法对电能质量信号重构的效果,引入能量恢复系数(ERP)、均方根误差百分值(MSE)、重构信噪比(SNR)重构评价指标。对各种电能质量扰动信号分别进行100次仿真重构实验,通过式(4)、式(5)、式(6)求平均值,得到电能质量信号重构性能评价指标如表1所示,研究所提出的算法对电能质量扰动重构效果较好。 (1)能量恢复系数(ERP): (4) (2)重构信噪比(SNR): (5) (3)均方根误差百分值(MSE): (6) 表1 电能质量信号重构性能评价指标 在相同的傅里叶稀疏基和二元块对角观测矩阵的情况下,将所研究算法与SAMP算法、CoSaMP算法对电能质量信号进行重构实验,进行多个方面对比分析。以电压闪变为例,分别进行100次仿真重构实验,在相同的仿真实验条件下,上述三种重构算法的ERP、SNR、MSE以及运行时间如表2所示。由表2中数据分析可知,在对电能质量信号进行重构时,研究提出的CoSaSAMP算法与SAMP算法、CoSaMP算法相比,在ERP、SNR、MSE、运行时间方面都有不同程度的优势。CoSaSAMP算法在稀疏度未知的情况下,保留了CoSaMP算法重构效率高、运行时间短的优点;与SAMP算法相比,减少了信号的迭代次数,降低了算法运行时间,提高了重构精度。 表2 三种算法重构性能对比 以电压闪变电能质量信号为例,在不同稀疏度和不同测量值条件下使用三种算法对原始信号精确重构概率曲线。稀疏度K从20递增到70,三种算法在相同条件下仿真实验100次,通过计算平均值得到精确重构概率曲线如图8所示。从图8中可以看出,CoSaSAMP算法与SAMP算法曲线相近,在相同精确重构概率下CoSaMP算法对应的稀疏度要大于其他两种算法,这是因为其他两种算法的设计思想是自适应调整稀疏度,最终得到的稀疏度要小于真实稀疏度,而CoSaMP算法是在稀疏度已知且为真实稀疏度条件下运行。稀疏度K固定值为30,测量值M从50变化到120,三种算法在相同条件下仿真实验100次,通过计算平均值得到精确重构概率曲线如图9所示。从图9中可以看出,在相同重构概率下,CoSaSAMP算法的测量值M要小于其他两种算法。因此CoSaSAMP算法相比于SAMP算法、CoSaMP算法具有较好的重构效果。 图8 不同稀疏度下精确重构概率 图9 不同测量值下精确重构概率 在CS理论的基础上,提出了一种用于电能质量信号压缩重构的CoSaSAMP算法,在稀疏度未知的情况下,通过稀疏度自适应调整和递归思想实现电能质量信号的精确重构。仿真结果表明,用所提出算法重构电能质量信号时,信噪比SNR均高于35 dB,能量恢复系数ERP达到99.6%以上,最小均方误差MSE在2%以内;在相同条件下,CoSaSAMP算法的重构信噪比、均方误差百分比和能量恢复系数优于CoSaMP算法和SAMP算法;在相同傅里叶变换稀疏基下,测量矩阵为二元块对角矩阵,与高斯随机矩阵相比,测量矩阵与稀疏基的相干性小,电能质量信号的重构效果更好。研究提出的CoSaSAMP算法在稀疏度未知的情况下,具有抗噪能力强、鲁棒性能强、重构效率高的优点,降低了算法运行时间,提高了电能质量信号的压缩重构精度。
1.2 信号稀疏表示
1.3 测量矩阵
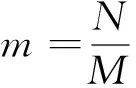
2 重构算法



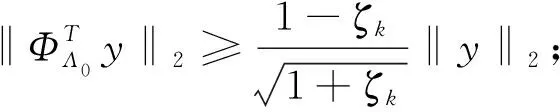
3 仿真实验
3.1 稀疏度估计
3.2 重构效果


3.3 重构性能对比


4 结论

