两阶段随机线性优化问题的等价形式

王 炜，李忠伟，王丹丹

（辽宁师范大学 数学学院，辽宁 大连 116029）

随机规划是一类含有随机因素的数学规划问题。在数学规划问题的模型中引入随机变量，能够使模型更加符合实际情况，从而使决策更加合理。极小极大随机线性优化问题是由Žáčková[1]率先提出的。求解极小极大随机优化问题的算法包括样本均值近似法[2]、基于梯度法[3]、切平面算法[4]和椭球算法[5]等。本研究在概率分布集合由一阶矩和二阶矩刻画时，将两阶段极小极大随机线性优化问题转化为为半定优化问题。

面对各项系数都含有随机变量的规划问题时，往往需要在观察到随机变量的实现之前作出决策，会导致某些决策不满足约束条件。此时，通常需要建立和引入二阶段有补偿的问题模型，既可以使决策满足约束条件，又可以使损失惩罚达到最小。本研究拟引入带有固定补偿的极小极大两阶段随机线性优化问题模型[6]解决含有随机变量的数学规划问题，如式（1）所示。

其中，

x为一阶段决策变量，二阶段决策变量w取自集合X(x) ={x ∈Rn:Ww= h - Tx,w ≥0}，W为补偿矩阵，T为影响随机变量ξ的一个参数矩阵，h为常量。P为随机参数ξ的概率分布，在实际应用中一般不能精确地求得，所以通常用概率分布集合P上第二阶段期望成本的最大值来处理概率分布的不确定性。

为了使模型更接近实际，从而得到更加可靠的数值解，通常将风险考虑到模型中。风险建模的方法是在二阶段成本中采用一个效用函数U(·)，如式（2）所示。

其中，效用函数U(Q(x,ξ))为置信水平为ε的最坏情况下的条件风险值

因此，式（2）即为本文要研究的两阶段随机线性优化问题的目标函数。

设μ ∈Rk是均值，Σ ∈Sk是协方差矩阵（Sk为k 维对称矩阵的集合），为了保证二阶期望成本EP[U(Q(x,ξ))]有定义，假设μ,Σ是有限的，且Σ ≻0，则由一阶矩和二阶矩描述的所有概率分布构成的集合可表示为

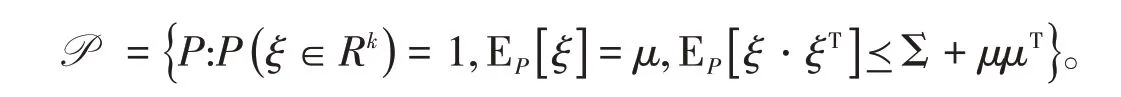
A ≻0 表示A 是正定矩阵，A-≻0 表示A 是半正定的。同理，A ≺0 表示A 是负定矩阵，A-≺0 表示A 是负半定的。

1 目标函数的内部极大化

考虑式（2）的内部极大化问题

假设该优化问题的概率分布P对应的测度为F，则式（3）就等价为

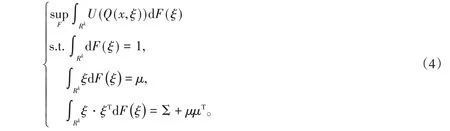
引入Lagrange乘子ζ ∈R,η ∈Rk,G ∈Sk，则式（4）的Lagrange函数为

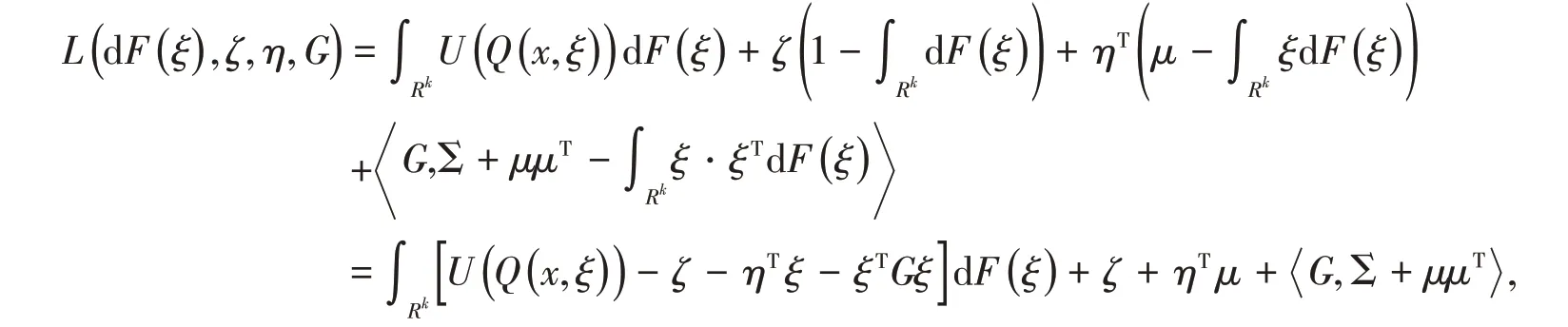
其中，矩阵A,B的内积定义为A,B = tr(ATB)，tr(· )表示矩阵的迹。由强对偶定理[7]可知

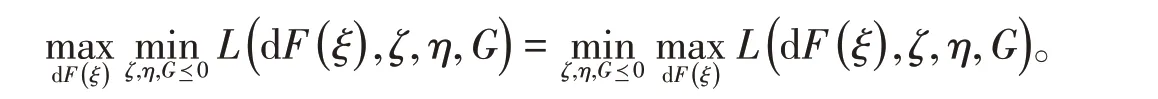
因此，式（4）的对偶问题为

2 效用函数的等价形式

由条件风险值的定义

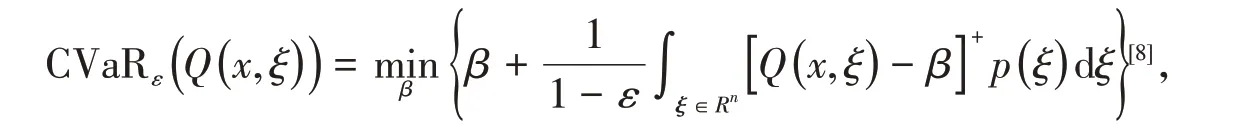
可得

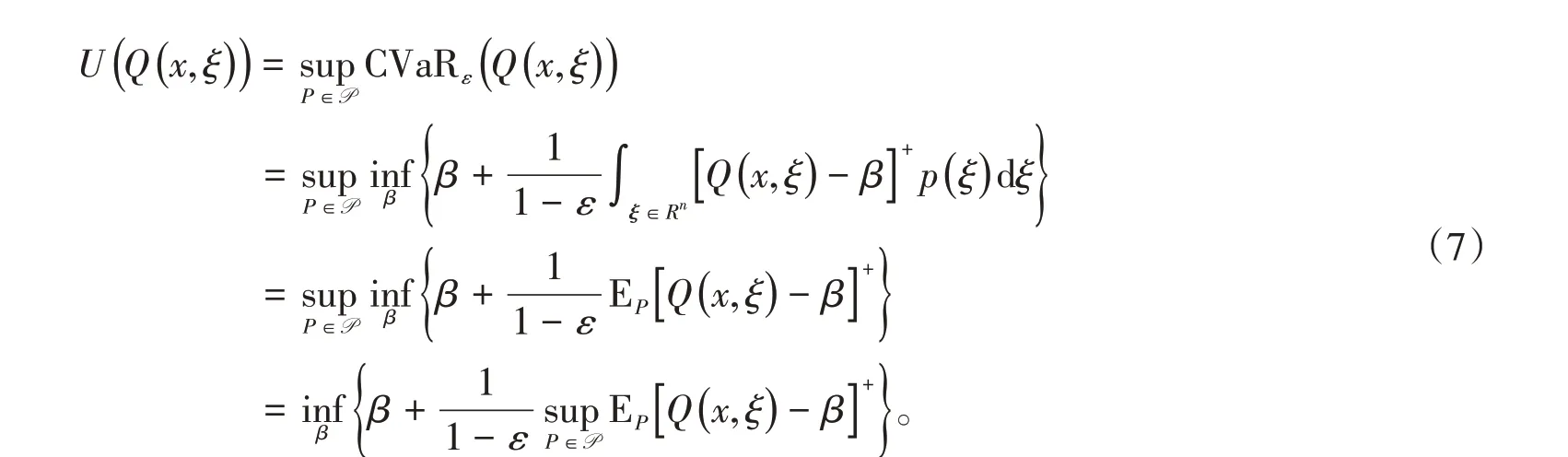
引入Lagrange乘子y0∈R,y ∈Rk,Y ∈Sk，则式（7）中的极大值函数

可得式（8）的对偶问题为

式（10）中的约束可以写成两个等价的约束

3 结论

将式（14）代入式（6）的约束[ξT1]H[ξT1]T≥U(Q(x,ξ))中，可得

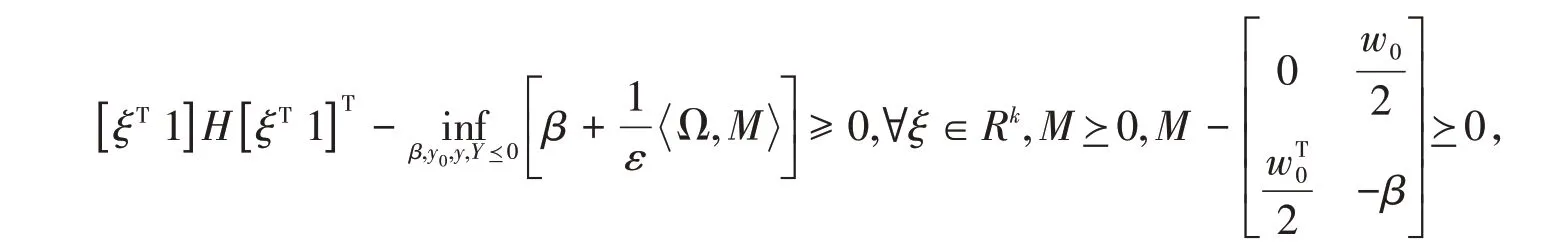
即

上式又等价为

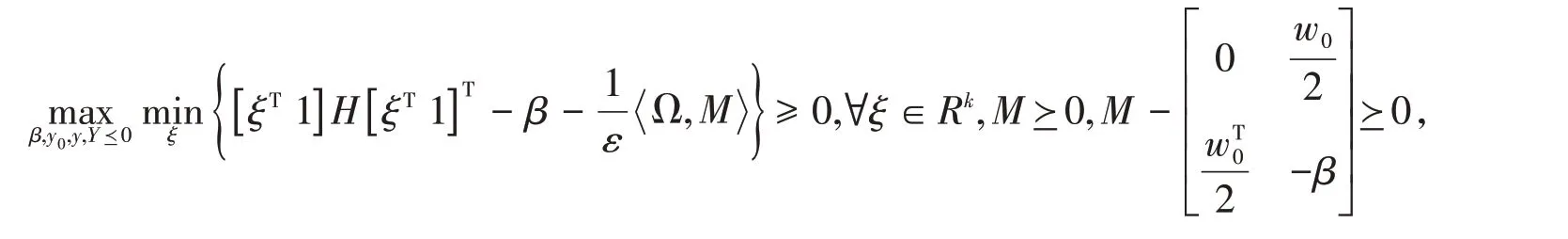
即

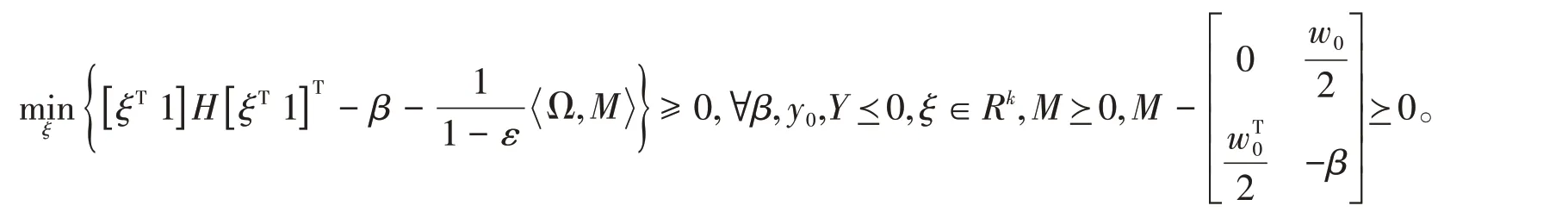
因此

综上所述，问题（2）最终可以转化为

把Ω、H、M带入问题（15）中得半定规划问题