解含多个复杂分量函数无约束minimax问题的积极集光滑化算法

周正勇,秦丽娜

(山西师范大学数学与计算机科学学院,山西 临汾041004)

1.引言

本文考虑如下无约束minimax问题:

其中分量函数fj:,复杂且二次连续可微,q较大.问题(1.1)是一类典型的不可微优化问题,在数据拟合[1],工程设计[2],结构优化[3],资源配置[4],选址问题[5],电路设计[6]等领域有广泛的应用,此外,曲线拟合问题,L1和L∞逼近问题等均可等价转化为该类问题.

由于问题(1.1)的非光滑性,光滑优化的理论与算法不能直接用于求解该类问题.解该类问题的一类方法是将其等价转化为如下光滑约束优化问题:

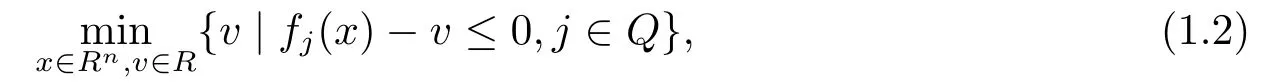
进而用求解一般光滑约束优化问题的算法对(1.2)进行求解.文[7]指出该类方法有两个缺点,首先,该问题中Lagrange函数的海森矩阵通常奇异;其次,目标函数v可由αv替代,其中α是任意大于0的常数,因而目标函数可被任意尺度化,从而该问题病态.另一类方法是非光滑优化方法,如次梯度法,割平面法,捆集法等.但这类方法大多是基于非光滑凸问题建立的,其收敛性条件较强.

解问题(1.1)的第三类方法是光滑化方法,该类方法通过构造max函数的光滑逼近函数(一般采用凝聚函数[8]其中p >0为光滑化参数),将问题(1.1)转化为一族带光滑化参数的光滑无约束优化问题:

当p趋于∞时,这族带光滑化参数的优化问题的稳定点趋近于问题(1.1)的稳定点.由于问题(1.3)为光滑无约束优化问题,因此可采用许多解光滑无约束优化问题的算法对其进行求解.

直接计算,凝聚函数的梯度及海森矩阵为:

其中

由于凝聚函数的梯度与所有分量函数的梯度相关,海森矩阵与所有分量函数的梯度及海森矩阵相关且表达式较为复杂,因此,当分量函数复杂且个数较多时,凝聚函数的梯度及海森矩阵的计算量较大.为了改善这一问题,文[9]构造了如下方程:

构造了一种积极集策略的光滑化max函数αt(x):,该函数仅与函数值较大的分量函数相关.文[9-10]均采用迭代策略计算αt(x)的函数值及与其相关的分量函数的指标集,计算效率较低.

本文对文[9]中基于方程(1.4)及函数(1.5)构造的积极集策略的光滑化max函数,给出了指标集的直接计算方法,利用该指标集将方程(1.4)转化为一般的三次多项式方程,根据该三次多项式方程根的性质给出了αt(x)的一种稳定计算策略.结合Armijo线搜索,负梯度和牛顿方向及光滑化参数的更新策略,给出了一种解含多个复杂分量函数无约束minimax问题的积极集光滑化算法,初步的数值实验表明了该算法的有效性.

本文用到的假设和引理.

假设1.1fj(x),j ∈Q,二次连续可微.

引理1.1[9]对任意的t >0,(1.5)式及方程(1.4)的解定义了一个二次连续可微的光滑化max函数αt(x),且αt(x)满足

引理1.2[9]对任意的x ∈Rn,t>0,αt(x)仅与如下的指标集相关:

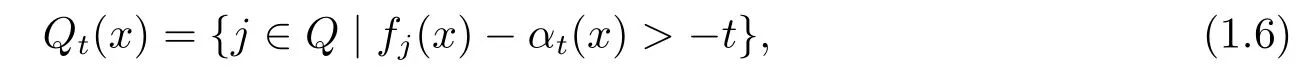
2.指标集Qt(x)的直接计算方法

3.积极集光滑化max函数的稳定计算策略

证由(3.4)及(3.5)式可得

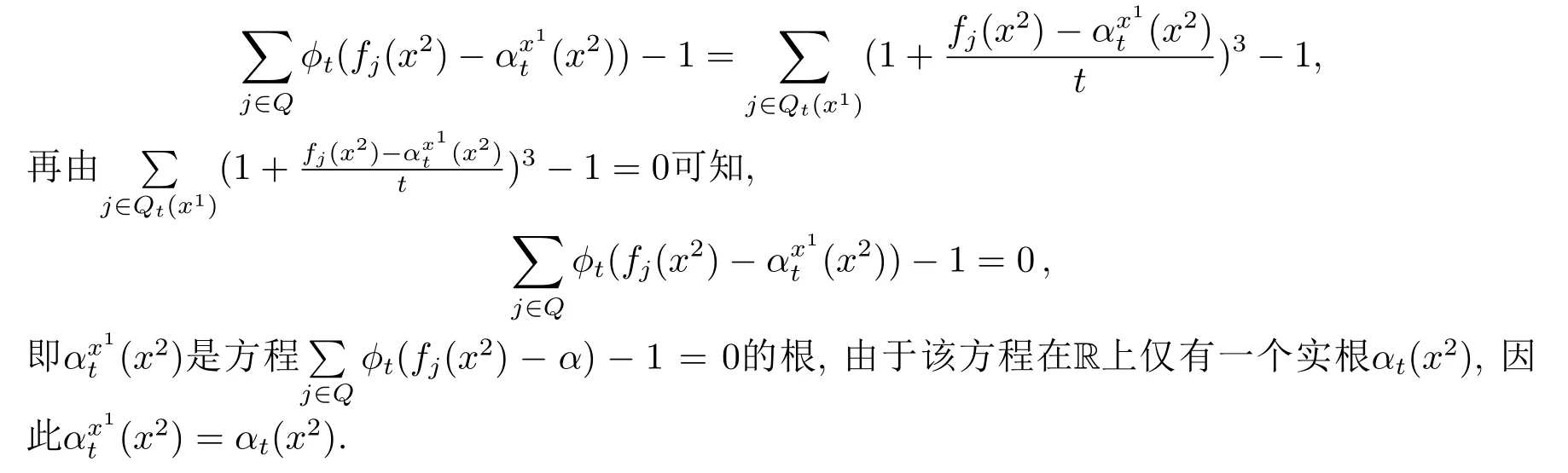
4.积极集策略的光滑化算法及其收敛性

本节基于前两节给出的积极集策略的光滑化max函数αt(x),结合文[11]中的Newton-Armijo算法,给出一种解含多个复杂分量函数无约束minimax问题的积极集策略的光滑化算法.

算法4.1

5.数值实验

本节将文[11]中基于凝聚函数提出的第二种解无约束minimax问题的算法记为PRW2,其光滑化参数采用与算法4.1对应的更新策略pk+1=pk/ω.本节选取了两个梯度及海森矩阵较为复杂的半无限minimax问题,将其等距离离散化后得到两类含多个复杂分量函数的无约束minimax问题,将算法4.1同算法PRW2进行了数值比较.算法在MATLAB R2014a中编程实现,在配置为INTEL(R) Core(TM) i5-6200U 2.30GHz,内存为4.00GB的笔记本上运行.数值结果表明,对含多个复杂分量函数的无约束minimax问题,算法4.1的稳定性与计算效率均高于算法PRW2.

例5.1[12]

例5.2[12]

算法4.1的参数设置如下:

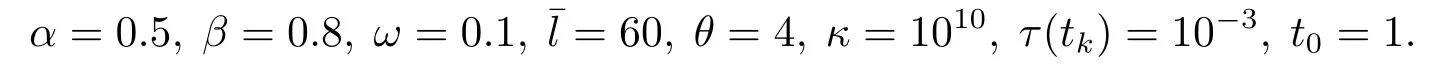
终止准则为

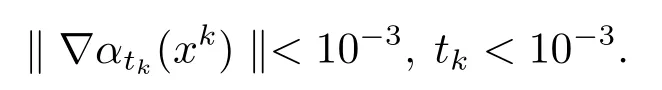
相对应的将算法PRW2 的终止准则设为

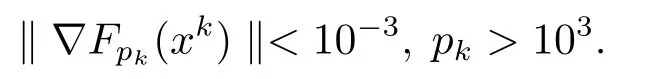
例5.1及例5.2等距离离散化后分量函数的个数分别取2.5k1×105(k1=1,......,40)与2k2×103(k2=2,......,40).在算法PRW2中,当计算机内存溢出时,算法停止.

图5.1给出了例5.1及例5.2在不同离散程度下算法4.1与算法PRW2的总迭代时间.由图可知,两者的总迭代时间基本随着分量函数个数的增加呈上升趋势,且算法4.1的总迭代时间均比算法PRW2的总迭代时间少.随着分量函数个数的增加,算法4.1的总迭代时间增长稳定性较好,而算法PRW2稳定性较差,例如在例5.2中,当分量函数个数为1.2×104,3×104和3.2×104时,算法PRW2的迭代次数分别为86,68和60,总迭代时间分别为3.80秒,6.37秒和5.53秒,而其它离散化问题的迭代次数介于4650到5489之间,总时间介于176.02秒到1029.10秒之间.

图5.2给出了例5.1及例5.2在不同离散程度下算法4.1与算法PRW2的平均迭代时间.由图可知,算法4.1的平均迭代时间均比算法PRW2的平均迭代时间少.算法4.1在例5.1中平均时间较高的离散问题有8个,对应分量函数的个数为6.5×106,6.75×106,7×106,7.25×106,7.5×106,7.75×106,8×106,8.25×106,分量函数赋值次数分别为39,40,41,43,56,48,57,54,梯度赋值次数分别为13,13,13,13,14,15,18,21,海森矩阵赋值次数及迭代次数分别为9,9,9,9,10,11,14,17,平均迭代时间分别为10.58秒,11.67秒,12.09秒,12.87秒,13.40秒,11.71秒,10.84秒,9.87秒,而其它离散化问题的分量函数赋值次数为41或42,梯度赋值次数为23或24,海森矩阵赋值次数及迭代次数为19,20或21,平均迭代时间介于3.10秒到7.04秒之间.此外,由图5.1及5.2可知,当例5.1及例5.2中分量函数的个数分别大于4×106和4×103时,由于计算机内存溢出,算法PRW2 失败.

图5.1 算法4.1与算法PRW2 总迭代时间

图5.2 算法4.1与算法PRW2 平均迭代时间

图5.3 算法4.1中相关分量函数的个数与q的平均比例

图5.3给出了例5.1及例5.2在不同离散程度下算法4.1中相关分量函数的个数与q的平均比例.由图可知,随着分量函数个数的增多,相关分量函数的个数与q的平均比例总体呈递减趋势,例5.1及例5.2在算法4.1的迭代中相关分量函数的个数平均比例不超过11%和3.5%.因此,当分量函数较多且复杂时,算法4.1仅需计算少部分分量函数的梯度及海森矩阵,而算法PRW2在每次迭代中均需计算所有分量函数的梯度及海森矩阵,因此,算法4.1的计算效率优于算法PRW2.