HPM视角下的分配问题学习进阶设计

姜浩哲 汪晓勤

(华东师范大学教师教育学院 200062)

1 问题的提出

2017年6月，由美国数学及其应用联合会(COMAP)、工业与应用数学学会(SIAM)联合编写的《数学建模教学与评估指南》一书中明确提出了“数学建模应当在学生数学教育的每一个阶段都被教授”、“从学前到大学开展数学建模是可行的”等观点[1].但是在目前各学段的数学教育中，现实情境通常以应用题的形式作为练习让学生巩固所学数学知识[2]，数学建模课程缺乏有效的组织形式和系统的教学资源，建模内容间也缺乏必要的联系.

美国国家研究理事会(National Research Council，简称NRC)在研究中发现大多数课程内容的主题间缺乏连贯性和系统性，课程设计忽视了学生对同一主题的理解不断提升和深化的过程，而重复、浅显、间断地学习某一主题会阻碍学生知识基础的夯实[3].为此，NRC提出学习进阶(Learning Progressions)(1)Learning Progressions与Learning Trajectories本质上具有一致性，因而在此可不做区分(参阅文献[4]和[5]).有关概念，将其定义为“在一个较大时间跨度内(例如6至8年间)，学生对某一主题的思考和认识不断丰富、精致和深入的一种过程”，旨在揭示学生在相当长时间内学习和研究某一主题思考、理解和实践活动的认知发展：由浅入深、从简单到复杂、从零散到全面、从低水平到高水平[5].学习进阶为数学建模系统、一致、连贯地贯穿于不同学段数学课程和有效衔接相邻学段间数学建模教学提供了科学方法.

在大、中、小学的数学课程内容中，常常出现一类关于如何将给定资源(如经济资源、权力资源等)按一定的方案、要素或准则(如按比例要素等)分配给若干对象的问题.例如，在小学阶段，《义务教育数学课程标准(2011年版)》明确要求学生“在实际情境中理解比及按比例分配的含义，并能解决简单的问题”[6]；在初中阶段，用方程组解应用题中就有不少分配问题；在普通高中阶段，分配问题会与古典概型有关内容相联系；大学本科阶段，席位分配问题往往是各类数学建模课程的重点内容.

在数学史上，分配问题自公元1世纪就引发了数学家的关注，并在此后的众多实际运用中经历了发展、完善和优化的过程.我国古代数学名著《九章算术》中的衰分术详细记载了古代农业、征役、行商中的按比例分配问题[7].17世纪，帕斯卡(B. Pascal, 1623—1662)与费马(P. Fermat, 1601—1665)通信讨论赌金分配的“点数问题”标志了概率论的诞生[8].1880年，美国众议院的席位分配悖论产生后，亨廷顿(S. P. Huntington, 1927—2008)等数学家更是一度寻求新的分配方法和模型[9].

荷兰学者Bakker认为，历史现象学可以为建立和发展假设的学习进阶(Hypothetical Learning Trajectories)理论提供准备[10].有鉴于此，我们希望以分配问题发展史为依据和参考建立假设的学习进阶，使数学建模教学能围绕主线、不断深入，贯穿在小学至大学的课程中，与学生的认知发展齐头并进.同时，教学设计从HPM视角切入，引导学生经历分配问题逐渐复杂、数学模型逐渐完善的过程，既感受数学的历史，感悟数学的文化，又加深对模型本质、建模过程的认识和理解.

2 教学设计

2.1 小学阶段分配问题的教学设计

2.1.1问题引入

例1早在公元1世纪，我国古代数学名著《九章算术》中就记载了大量农业、征役、行商中的按比例分配问题，古人称比例为“衰”，按比例分配为“衰分”.其中，有这样一道关于分派徭役的问题：“今有北乡算八千七百五十八，西乡算七千二百三十六，南乡算八千三百五十六，凡三乡，发徭三百七十八人，欲以算术多少衰出之.问各几何？”

2.1.2方法归纳

教师进而向学生解释：事实上，这就是一个简单的数学模型，可以把数学模型理解为数字、字母或其他数学符号组成的，描述现实对象数量规律的数学公式、图形或算法.

2.1.3思维拓展

教师展示《九章算术》中的问题答案：“北乡遣一百三十五人、一万二千一百七十五分人之一万一千六百三十七；西乡遣一百一十二人、一万二千一百七十五分人之四千四；南乡遣一百二十九人、一万二千一百七十五分人之八千七百九.”并向学生提出以下思考拓展问题：

思考题1：《九章算术》的问题答案在数学上没有任何问题，但是否符合实际？

思考题2：能否猜想古人实际会如何分派徭役？

思考题3：如果按照思考题2中你猜想的方法分派徭役，是否会对北乡、西乡或南乡造成不公平？三乡在理论上会因此分别多征派或少征派多少徭役人数？

在学生思考回答后，教师更进一步说明：由此可见，数学模型其实还是一种对实际问题的简单化、理想化表达.

在上述教学设计中，教师运用了选自《九章算术》的一段史料，学生对数学模型开始有了最初步的认识.小学阶段，大多数学生常常将数学模型理解为对现实问题复制式的数学表达，学生解决实际问题停留在直接运用教师帮助他们已经建立的数学模型，但数学史的运用使得学生发现数学模型不是现实原原本本的复制，而是数学化、理想化的产物，从对数学模型本质认识的层面上说，学习进阶的萌芽已经出现.同时，从思维拓展部分中可以发现，教与学源于史料，但又不唯史料，教师引导学生发现数学史料中脱离实际的内容，培养他们的批判性思维，为后续的学习进阶打下了认知基础.

2.2 初中阶段分配问题的教学设计

2.2.1新知传授

教师教授学生运用方程组求解应用问题的一般步骤.

2.2.2例题解析

教师引导学生回顾：在6年级，学生曾学习和解决了公元1世纪《九章算术》中一类简单的按比例分配问题.继而指出，现实生活中的许多分配问题，其分配所依据的比例并不会直接给出，而是需要根据已知条件间接求得.

例2(改编自《九章算术》)假设漆与油的售价之比为3∶4；油与漆可按4∶5的比例和成油漆.现有银两正好能购买3斗漆，问：该按什么比例分配银两来分别购买漆与油，使购得的漆与油恰可以和成油漆？如果现有银两正好能购买n斗漆呢？

再指导学生作答.

随后，教师再次引导学生回顾6年级时的按比例分配模型，发现例1的比例关系式同样可由方程组得出：对于未知量X,Y,Z，有方程组

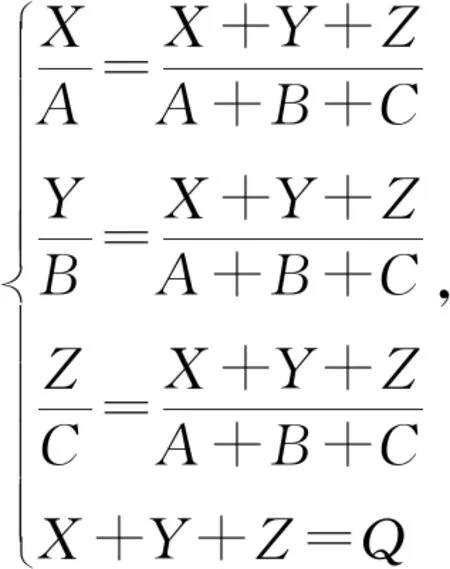
这时，教师向学生说明，两类看似不同的问题本质实际上却是统一的.

2.2.3课堂总结

课堂最后，教师指出，从简单运用已建立的模型到根据一般步骤自主建立模型，这一阶段的学习让学生对数学建模有了更进一步的尝试.再看数学模型，小学阶段，数学模型曾被认为仅仅是用来解决实际问题的，它只是具有应用价值，但如今，教师引导学生发现，数学模型还是对现实情境的一种简洁、清晰的表达，两道例题中的寥寥几个等式，却有数行文字的内涵，这也很好地解释了人们常说的“数学是一种语言”.

运用方程组求解应用问题是一个简单的数学建模过程，在初中数学课堂，教师往往会教授学生运用方程求解应用问题的一般步骤，此时的数学建模有固定的模式和方法作为参照，但学生开始能够独立完成建立模型和求解模型这两个十分重要的步骤.无论从数学建模的水平上，还是对数学模型的理解上，学生都完成了一次学习进阶.

2.3 高中阶段分配问题的教学设计

2.3.1问题引入

在学习了概率论的有关知识后，教师告诉学生其实概率论的起源也与分配问题有关.

例3赌技相当的甲、乙二人各出96金币，规定必须要赢p场者才能赢得全部赌金共192金币，但比赛中途因故终止，且此时甲乙胜局数为n:m.若你是仲裁者，请问此时应如何分配赌金，并说明理由.

教师要求学生根据小学和初中时期对数学模型的认识，以小组合作讨论的形式，为甲和乙确定一种合理的分配方案，并求得分配结果.

2.3.2历史展示

教师告诉学生，本题的背景就是17世纪帕斯卡和费马通信往来中研究的赌金分配问题.教师指出：在历史上，数学家们也对这个问题进行了激烈的讨论，许多数学家都给出了自己的解答.教师向学生加以展示：

表1 赌金分配问题中的数学家解答

教师对上述方法依次作出解释和评价.

2.3.3课堂总结

最后，教师作适当总结：与小学和初中所认识的应用数学模型解决实际问题不同，这一次，数学家们没有直接得到数学模型，而是在逐步调整、修正模型过程中找到了真理.1654年，帕斯卡在他的《论算术三角形》中给出了正确的赌金分配问题一般公式，才结束了模型从错误到正确的漫长发展历程.教师也向学生强调：数学模型其实并不唯一，无论是历史上费马、帕斯卡、惠更斯的方法，还是今天部分同学给出的直接计算甲、乙获胜概率的方法，他们都是有理有据的正确模型.

高中阶段，数学模型开始走向多元、开放，运用不同数学方法可以建立不同的模型，模型所联系的知识点也不再单一.在对数学模型的理解上，通过数学史的融入，教师引导学生发现数学模型不是一蹴而就的，而是在数学家们不断调整、修正中逼近真理的.同时，学生开始在没有模式参照的情况自己探索建模方法，这是建模能力进阶过程中的一个重要台阶.

2.4 大学本科阶段分配问题的教学设计

2.4.1回顾历史背景

教师引导学生回顾：在6年级时，学生曾研究过《九章算术》中一道关于分派徭役的按比例分配问题，当时学生曾在教师的引导下将数学模型理解为对现实情境问题的一种简单化、理想化表达，知道《九章算术》给出的分配结果解答在实际生活中是不可能实现的.但是，数学模型从实际问题中来，终归还是要回到实际问题中去，而这样的分配难题在实际问题中似乎并不可以避免.表2是思考题2的一种常规解答，即参照惯例，可以把各乡按比例分配后的徭役名额近似地保留一位小数，将无法细分的一个徭役名额分派至十分位数值最大的地区.

表2 按照比例并参照惯例的徭役分派

2.4.2展示历史上的悖论

教师指出，在历史上，表2的解法也是汉密尔顿(A. Hamilton, 1755-1804)的想法，被称为最大剩余法(Greatest Remainders，简称GR).事实上，1850年至1900年间，美国国会众议院席位分配就多次出现了与公元1世纪《九章算术》中记载的相类似的情形，这种模型也被当时采用.但是，1880年，关于亚拉巴马(Alabama)州的席位分配难题将GR法推上了风口浪尖：由于美国总人口数的增加，国会众议院的总席位数从1787年的65逐渐增加到1920年的435，但是，亚拉巴马州却在该州人口占美国总人口比例不降低的情况下，因众议院总席位增加分得的席位反而减少，这就是历史上著名的席位悖论[9].教师用以下表格模拟这种情况.

表3 当总席位数增加时按照比例并参照惯例的席位分配

教师引导学生发现，A州的人口比例没有发生变化，但当总席位增加1时，其分得的席位数反而减少了，并指出：这样不公平的分配人们是难以接受的，更加不公平的问题还有！

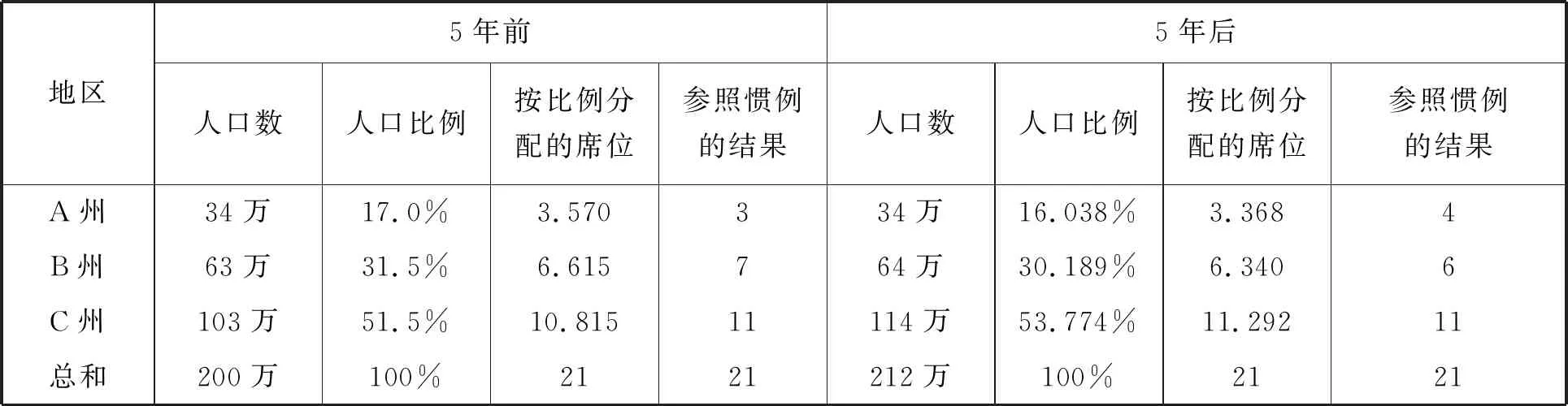
表4 当人口数增加时按照比例并参照惯例的席位分配

教师再次解释说明，B州的人口数增加却比原来少了1席，A州的人口数未变却比原来增加了1席！历史上，GR法的这一重大缺陷称之为人口悖论[9].

2.4.3新探历史旧题

教师指出：由此可见，数学模型不能仅仅凭直觉或感性的认识构造，它必须包括严谨的数学论证，拥有严密的数学结构，数学模型必须要让我们看到问题的本质.席位有可能无法按照人口比例精确分配，就有可能会出现不公平现象，但我们应该努力去寻找一种衡量不公平的数量指标，通过计算和比较数值大小把不公平度降到最低.在找到问题的突破口后，教师提到，学生曾在6年级思考题3中计算过三乡在理论上分别多征派或少征派多少徭役人数，这其实就是一种衡量绝对不公平的指标.学生曾在初中学习了相对和绝对的概念，教师自然而然地引导学生借鉴并建立一种衡量相对不公平的指标.在学生适当讨论后，教师介绍亨廷顿除数法席位分配模型基本构想.

2.4.4再现历史解答

教师指出：高中时期，费马、帕斯卡、惠更斯等数学家们都曾给出了赌金分配问题的精彩解答，学生第一次看到了数学文化的多元、开放与包容.在今天所学习的席位分配模型中，历史上的许多数学家同样曾“心有灵犀”地探寻过亨廷顿除数和不公平度的衡量指标[11].教师向学生展示表5.

实际上，早在6年级时，席位分配问题的雏形就已出现，教师曾通过引导学生关注“《九章算术》中也有脱离生活实际的内容”这一情况，为大学阶段激发学生的认知冲突埋下了伏笔.重新审视席位分配模型，可以发现其实质就是《九章算术》中按比例分配模型在政治选举领域优化、发展、完善了的“进化体”，只是这样的优化、发展、完善过程联系了更多的数学知识，需要有更高的数学水准、更强的应用能力.通过数学史的回忆、再现和演绎，教师加深了学生对数学模型本质的理解：数学模型不是单一、静态、固定、一成不变、事先预制好的，而是多元、动态、开放、灵活多变的，当数学模型从一个领域转移到另一个领域时，它就必须经历修正、调整的过程以适应新的问题情境.同时，关于亨廷顿除数和不公平度的衡量指标建立，数学史上也再次呈现了“百花齐放”的格局，展现了多元文化的魅力.

3 数学史与学习进阶的融合

纵观从小学至大学的分配问题教学设计，数学史通过复制式、顺应式和重构式融入数学教学，且教师在不同学段教学中运用的数学史既有相互照应、补充，也有相互抵触、矛盾，既是为了与学生的认知发展相匹配，也是为了在创造学生认知冲突的过程中激发学生主动探索新知的欲望.而在数学史料和问题的不断回顾、补充、对比中，学生的认知和元认知水平均能得到促进[12].实际上，数学史是在整体性重构后与学习进阶相融合的，如表6所示.

表6 数学史与学习进阶融合的方式

4 数学史与学习进阶融合的价值

在分配问题的教学设计中，不仅融入数学史体现了“文化之魅”，而且融合了的数学史与学习进阶还共同体现了“知识之谐”、“方法之美”、“探究之乐”、“能力之助”和“德育之效”.

4.1 文化之魅

当跨越了近20个世纪，来自亚洲、欧洲和美洲不同地域，且与经济生活、社会生活等多个方面相联系的分配问题发展历史在教学中展现时，学生能充分感受到数学的“文化之魅”.

4.2 知识之谐

一方面，基于赌金、席位分配问题的历史相似性或历史上数学家们的认知引导学生发现和解决问题，使得学生理解和学习模型有关知识的过程变得自然而然、水到渠成；另一方面，基于学习进阶的教学是依据学生的认知和理解而设计的，各学段的学习有赖于之前学段的知识内容，学生也能明白有关模型或知识不是“降落伞”从天而降，并亲身经历了知识不断补充、发展、完善的过程，体现了“知识之谐”.

4.3 方法之美

一方面，历史上众多数学家们关于赌金、席位等分配问题或合理完美、或有待完善的思想与方法，都拓宽了教与学过程中师生的视野，成为了今天数学建模发展的宝库.另一方面，分配问题的数学模型不断发展、完善，并适用于更多全新的领域，其所联系的数学方法也不断增多.在学习进阶中，不仅学生不同学段所学的许多或简单、或复杂的思想与方法相互联结在了一起，而且不同数学分支或领域的方法能有机统一地在分配问题教学中呈现，“方法之美”跃然于课堂之中，更全面、丰富、系统的知识网络和体系也得以被学生深刻理解.

4.4 探究之乐

一方面，探究历史问题时，学生既能因与历史上数学家的解法相似而收获成功体验，也能基于历史主动分析和改进数学家的错误并探索新的合理方法，在数学活动经验的积累中收获乐趣.另一方面，在学习进阶中，教学始终围绕分配问题不断深入，学生经历着从面对复杂问题到完善解决方案的循环过程，6年级时思考和解答的不完美更是成为了推动大学问题探究的直接动力.随着问题情境的不断发展，“探究之乐”也因而愈发浓烈.

4.5 能力之助

一方面，历史问题有助于提升学生数学建模等核心素养[13]，数学史也为数学建模提供了真实的问题情境，而将真实情境数学化并检验不同模型实用性的数学建模和数学应用任务能有效发展学生一系列不同的数学能力[14].另一方面，学习进阶为循序渐进地引导学生发展建模能力提供了科学依据.从简单运用模型，到依固定步骤建立模型，再到独立自主全过程建模；学生数学建模能力不是一蹴而就的，基于学习进阶的教学也无疑成为“能力之助”.

4.6 德育之效

一方面，历史上数学家们锲而不舍追求真理的精神鼓舞了今天课堂中的学生；另一方面，基于学习进阶的教学也促进了学生的道德发展.早在先秦时期，我国《论语·季氏》就记载了孔子“不患寡而患不均”的政治主张，公平公正一直以来都是伦理道德的核心范畴.从按比例分配到席位分配，学生由依照和执行公平分配方案向研究和制定公平分配方案逐渐转变.当面对的现实问题越发复杂时，教师帮助学生加深了对于公平实质的认识和感悟，潜移默化的“德育之效”也由此达成.