基于分阶段ARMA模型的东莞市GDP数据分析与预测

崔志涛， 方清鑫

(东莞理工学院城市学院 计算机与信息学院， 广东 东莞 523419)

国内生产总值(GDP，Gross Domestic Product)是对一个国家或地区在一定时期内国民经济生产活动总成果的一种计量，是按市场价格计算的一个国家或地区所有常住单位在一定时期内生产活动的最终成果[1]，是衡量一个国家(或地区)经济状况的指标。一组GDP数据是一个时间序列(按照时间次序排列的一组观测值)，使用时间序列分析方法中的ARMA模型对GDP数据进行分析建模，可以反映市场运行的规律，预测未来的经济发展。本文使用Eviews 软件分别对东莞1978—2015年GDP数据和1992—2015年GDP数据建立了ARMA模型(数据选自《2018年东莞统计年鉴》)，并进行了预测。

1 ARMA模型

英国统计学家G.u.Yule在1927年提出了AR模型，被认为是现代时间序列分析的起源。1931年英国统计学家G.T.Walker提出了MA模型与ARMA模型，三者一起构成了时间序列分析的基础[2]。模型数据具有宽平稳与方差齐性的特征。美国统计学家GE.P.Box和英国统计学家G.M.Jenkins在1970年出版的《Time Series Analysis:Forecasting and Control》为实际工作者提供了对时间序列进行分析、建模、预测、诊断的系统性方法，被认为是时间序列分析发展的里程碑。模型对于差分之后具有平稳性的数据可以建立ARMA模型。

1.1 AR模型

AR模型(Autoregressive Model )将序列当前值表示为滞后值和当前随机干扰的线性组合，称为自回归模型，AR(p)模型的数学表达式为：

(1)

φ0,φ1,…,φp是自回归系数，εt是白噪声序列(随机序列)[3]。令L为一阶延迟算子，Lyt=yt-1,则AR(p)模型可以写为：

(1-φ1L-φ2L2-…-φpLp)yt=Φ(L)yt=εt

(2)

如果特征方程：

Φ(L)=1-φ1L-φ2L2-…-φpLp=0

(3)

的根都在单位圆外，则模型是稳定的。

1.2 MA模型

MA模型(Moving Average Model)将序列的当前值表示为当期和前期随机误差的线性组合，称为滑动平均模型，MA(q)模型的数学表达式为：

(4)

φ1,φ2,…,φq是滑动平均系数，记为yt=Ψ(L)εt。模型可逆的条件是滑动平均系数的特征多项式：

Ψ(L)=1-φ1L-φ2L2-…-φqLq=0

(5)

的根都在单位圆外。

1.3 ARMA模型

ARMA模型(Auto-Regressive and Moving Average Model)将序列当期值表示为当期及前期的随机误差与前期值的线性组合，ARMA(p,q)模型的数学表达式为：

(6)

记为Φ(L)yt=Ψ(L)εt，特征方程:

Φ(L)=1-φ1L-φ2L2-…-φpLp=0

(7)

与

Ψ(L)=1-φ1L-φ2L2-…-φqLq=0

(8)

的根都在单位圆外保证模型的平稳与可逆。q=0时，ARMA(p,q)为AR(p)模型；q=0时，ARMA(p,q)为MA(q)模型。

时间序列分析由观测数据的邻近依赖性构造一个预测函数，使得观测值与预测值之间的均方误差尽可能的小。使用矩估计、最小二乘估计、极大似然估计等[4]方法估计自回归系数与滑动平均系数。

2 ARMA(p,q)建模步骤

1)模型数据的平稳性。一个时间序列{Xt,t∈T}如果满足：

(9)

则称{Xt}是宽平稳时间序列(二阶矩平稳序列，协方差平稳)[2,4]，{γt}是{Xt}的自协方差函数。

可以用时序图方法与单位根检验的方法进行识别。

图1 对数二阶差分时序图

从时序图中可以看出，在对原数据取对数之后的二阶差分数据是平稳序列[5]。

2)模型数据的纯随机性。模型的数据为非白噪声序列，邻近观测值之间要具有相关性，也可以对源数据的差分序列进行检验。在Eeviews的命令窗口点击View/Correlogram，同时可以完成模型的定阶。

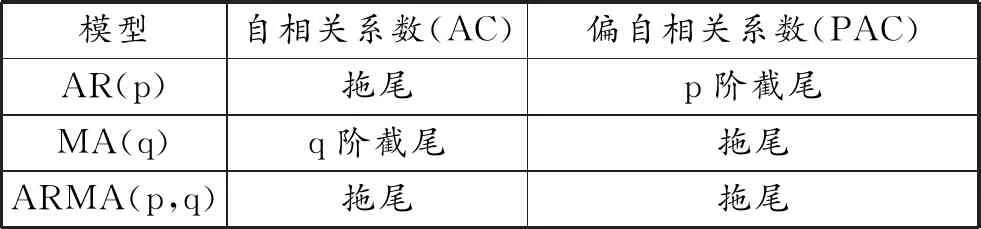
表1 自相关系数与偏自相关系数的性质

图2 对数二阶差分数据的自相关与偏自相关系数图

自相关与偏自相关系数均为拖尾，依据两倍标准差准则[2]模型定阶为AR(2)MA(1)。

3)模型的显著性检验。

由图3可以看出模型、系数均通过显著性检验，特征方程的根都位于单位圆内。

图3 ARMA(2,1)模型显著性检验

4)残差的白噪声检验。

图4 1978—2015年数据模型残差的白噪声检验

在5%的显著性水平下，残差全部为白噪声，可以说明数据的信息已经被充分提取。

5)预测数据。

表2 1978—2015年数据模型的预测数据

使用Eviews软件对未来数据进行预测，预测值与实际值的误差随着预测步长的增加而增大，验证了ARMA模型适合短期预测[6]。

3 1978—2015年东莞GDP数据分析

分析东莞市2018年统计年鉴中的1978—2015年GDP数据并计算年增长率。

图5 1978—2015年东莞GDP数据年增长率

1978—2015年东莞GDP数据整体呈现指数增长趋势，1992年东莞市的GDP首次实现百亿级别的突破，2002年实现千亿级别的突破。数据的年增长率呈现不规则趋势，极大值为1993年的41.6%，极小值为2009年的2.2%。结合我国改革开放的进程[7]以1978年为开始，1992年之后为一个新的时期。特别是在后一个时期内，社会主义市场经济得到了长足的发展，数据量可以体现出政策的效果。鉴于经济政策对时间数据产生了影响[8]，下文的模型选取了1992—2015的GDP数据进行了建模分析，数据二阶差分之后检验结果见图6。

图6 MA(1)模型的显著性检验

使用MA(1)模型得到预测数据如表3所示：

表3 1992—2015年数据模型的预测数据

对比1978—2015年数据模型的相对误差[9]减小，预测精度相对于1978—2015数据模型有所提高,模型参数简约[8]。

4 两个阶段数据的自相关系数对比

时间序列数据的自相关系数ρj反映了样本数据间的关联程度，定义为[4]：

(10)

矩估计为[4]：

(11)

使用样本数据计算得到自相关系数的估计，见表4。

表4 1978—2015年与1992—2015年两阶段GDP数据的1～5阶自相关系数

对比两段数据的自相关系数，1978—2015年GDP数据的1-5阶自相关系数要大于1992—2015年数据对应阶的自相关系数。

5 结论

本文分别建立了东莞市1978—2015年GDP数据与1992—2015年GDP数据的ARMA模型，并进行了数据的预测。对比1978—2015数据模型，1992—2015数据模型参数简约，预测精度高。计算两阶段GDP数据的1-5阶自相关系数进行对比，结果显示1978—2015年GDP数据的各阶自相关系数大于1992—2015年GDP数据的同阶自相关系数。