基于多项式拟合的中阶梯光栅光谱仪谱图还原
朱继伟,孙 慈,杨 晋,马婷婷,郭雪强,张 健
(1.长春长光格瑞光电技术有限公司,吉林 长春 130102;2.中国科学院 长春光学精密机械与物理研究所,吉林 长春 130033)
1 引 言
中阶梯光栅光谱仪因其高分辨率、高衍射效率在光谱分析领域中有着重要的应用[1-5]。中阶梯光栅光谱仪的主色散元件为中阶梯光栅,这种光栅具有低刻线密度、高衍射级次的特点,由于其自由光谱区很短,所以在应用时需要使用不同的衍射级次来实现宽的光谱范围。同时,中阶梯光栅存在很强的光谱级次重叠,通常需要其他色散元件实现级次分离[6],这种组合色散的方式,在像面上就形成了二维交叉色散光谱。这种光谱的接收像元与波长间并无直接关系可循,无法直接获得所需波长或波段的强度信息,须经过大量的分析计算,通过谱图还原算法,将二维图像信息转化为一维的波长与光强对应的光谱曲线,最终实现多元素的瞬时光谱分析。
传统的中阶梯光栅光谱仪的谱图还原算法是采用光线追迹法确定接收像面上像元与波长的对应关系。对于任意波长,结合中阶梯光栅光谱仪的结构参数可基于几何光学原理的光线计算,精确追迹出该波长在像面上的位置,但是中阶梯光栅光谱仪通常会使用上百个级次,光谱数据量十分庞大,因此这种算法追迹过程繁琐,计算效率有待提高[7]。近年来,长春光机所提出了一种基于公式归纳法的谱图还原算法,即结合中阶梯光栅光谱仪的光学设计参数,通过角度偏移近似建立简化的谱图还原模型,从而提高模型的建立速度和运算效率,经过多年的发展,这种算法已在工程上得到应用[8-11]。然而,随着应用要求的不断提高,中阶梯光栅光谱仪的光路设计越来越复杂,不仅结构形式多变,为校正各种像差,在光路中也会插入多个校正镜[12-15],从而这种简化模型的谱图还原算法在模型建立的难度上也在不断提高,运算速度也因此受到影响。
本文以采用中阶梯光栅和棱镜组合色散方式及采用柱面镜进行像散校正的中阶梯光栅光谱仪为研究对象,结合光线追迹方法,分别对中阶梯光栅光谱仪棱镜色散方向和光栅色散方向上波长与光斑的位置坐标进行多项式拟合,进而建立了波长与像元的对应关系,并将获得的谱图还原模型实际应用到中阶梯光栅光谱仪中。该算法计算过程简单有效,运算效率高,灵活性强,适用于各种中阶梯光栅光谱仪。
2 中阶梯光栅光谱仪
2.1 光路结构

图1 中阶梯光栅光谱仪光路Fig.1 Optical path diagram of echelle grating spectrometer
本文算法所采用的中阶梯光栅光谱仪的光路结构如图1所示。光束从小孔入射后经球面镜准直,以平行光形式入射到以准李特罗角放置的中阶梯光栅,经光栅色散后,由棱镜在垂直于光栅色散方向上继续色散,交叉色散后的光束通过球面反射镜,并经过具有校正像散作用的柱面镜后成像在CCD像面上。该中阶梯光栅光谱仪的技术指标如表1所示。

表1 中阶梯光栅光谱仪的技术指标
2.2 二维谱图
为避免级次重叠问题,中阶梯光栅光谱仪采用交叉色散的方式,通过辅助色散元件在面阵CCD像面上形成二维谱图,图2为中阶梯光栅光谱仪自由光谱区内的二维谱图示意图。其中,X方向为棱镜色散方向,Y方向为光栅色散方向,每条谱线对应一个光谱级次。谱图还原算法就是将像元位置与波长、级次一一对应,同时,通过CCD所获得的每个像元点的光强信息,建立起波长、级次与光强的一维谱图信息。图3为二维谱图转换为一维谱图的过程。

图2 自由光谱区内二维谱图示意图Fig.2 Schematic diagram of two-dimensional spectrogram in free spectrum region

图3 谱图还原过程示意图Fig.3 Schematic diagram of spectrogram reduction process
3 谱图还原算法
本文的研究对象为交叉色散式中阶梯光栅光谱仪,该光谱仪的中阶梯光栅具有偏置角,偏置角方向垂直于光栅色散方向,光束在偏置角方向上反射,在其垂直方向上色散,棱镜色散方向为水平方向。根据中阶梯光栅的锥面衍射方程[16]:
mλ=d·(sinα+sinβλ)·cosω,
(1)
式中:α为入射角,βλ为衍射角,ω为光栅的偏置角。各个级次的中心波长λcen为:
(2)
由此可知,不同衍射级次的中心波长在像面上垂直方向位置相同,而在仪器中不同波长在水平方向上的位置由棱镜决定。因此,棱镜与光栅的色散相互独立,分别决定各个波长在像面上的X坐标和Y坐标,可根据此特性在X方向和Y方向上分别建立拟合方程,获得波长与光线的位置关系。拟合原理如图4所示。

图4 谱图还原过程拟合原理Fig.4 Principle diagram of spectral reduction process fitting
3.1 棱镜色散方向
棱镜色散决定不同波长在像面上的X坐标,棱镜的色散方程[16]为:
(3)
式中:i0为棱镜入射角,φ为棱镜顶角,iλ为光线出射角,nλ为不同波长的折射率。在棱镜色散方向上,由于中阶梯光栅光谱仪的自由光谱区很小,不同波长可能对应着不同的光谱级次,但是不同波长的光线对应着不同的出射角,即在像面上X坐标位置不同,且在长波方向上级次间隔逐渐变小,在短波方向上,每个级次的斜率越来越大。本算法采用多项式拟合的方式对波长位置进行计算,可选择各个级次的中心波长建立X方向的多项式。具体拟合过程如下:
(1)选择N个不同级次的中心波长λm1-cen,λm2-cen,…,λmN-cen;
(2)追迹出这些波长的X方向位置,得到Xm1-cen,Xm2-cen,…,XmN-cen;
(3)根据坐标点(λm1-cen,Xm1-cen),(λm2-cen,Xm2-cen),…,(λmN-cen,XmN-cen)进行多项式拟合,得到多项式x=f(λ),由此可获得各个波长在像面上的X坐标。
为保证拟合多项式的准确性,在波长的级次选择上,长波波段采用的级次间隔比短波波段级次间隔大一些。
[56] Donald Rothwell, Freedom of navigation in the South China Sea: Australia must take a stand, Australian Strategic Policy Institute, June 14, 2017, https://www.aspistrategist.org.au/freedom-navigation-south-china-sea-australia-must-take-stand/.
3.2 光栅色散方向
光栅的色散方向决定光线的Y坐标,在该方向上,需计算出每一个级次自由光谱区内各个波长的Y坐标。由于使用级次较多,若逐一追迹每个级次的波长对应的成像位置,工作量太大。因此,本算法采用级次间拟合的方式,具体步骤如下:
(1)使用已选择的中心波长,其所处级次的自由光谱区为Δλm:
(4)
进而得到各级次自由光谱区域内其他4个波长值λm-max,λm-max1,λm-min,λm-min1,其中:
(5)
(6)
(7)
(8)
(2)追迹出以上波长的Y坐标,得到Ym-max,Ym-max1,Ym-min,Ym-min1;
从而可知任意级次的5个波长的Y坐标,得到每个级次的5个坐标点(λm-max,Ym-max),(λm-max1,Ym-max1),(λm-cen,0),(λm-min,Ym-min),(λm-min1,Ym-min1);
(3)根据获得的数据点坐标进行级次间拟合,取M个级次,则:由(λm1-max,Ym1-max),(λm2-max,Ym2-max),……,(λmM-max,YmM-max)进行多项式拟合得到y1=f(x);由(λm1-max1,Ym1-max1),(λm2-max1,Ym2-max1),……,(λmM-max1,YmM-max1)进行多项式拟合得到y2=f(x);由(λm1-min,Ym1- min),(λm2- min,Ym2- min),……,(λmM- min,YmM- min)进行多项式拟合得到y3=f(x);由(λm1-min1,Ym1- min1),(λm2- min1,Ym2- min1),……,(λmM-min1,YmM-min1)进行多项式拟合得到y4=f(x)。这样,通过上述式子可获得除已选级次之外的各个级次的5个相应波长的Y坐标位置;
(4)进行级次内拟合,通过上述过程可获得每个级次内5个点的Y坐标位置,即(λm-max,y1),(λm-max1,y2),(λm-cen,0),(λm-min,y3),(λm-min1,y4),在级次内对这些点进行多项式拟合,可得到Y=f(λ)。
进而可获得任意波长的Y坐标,其中,级次内的取点可根据实际情况进行增加或减少。
4 实验结果与分析
4.1 谱图还原算法精度实验
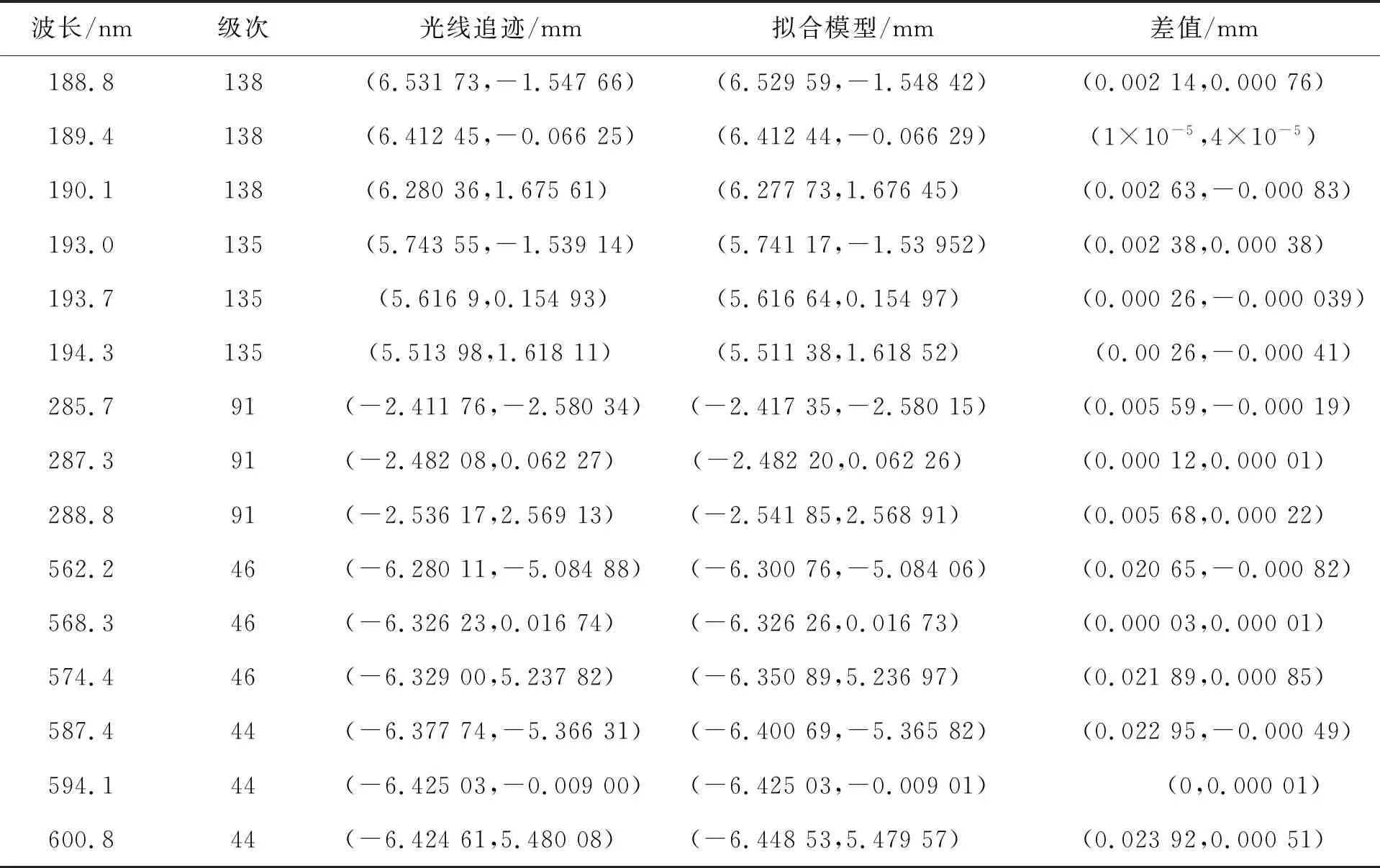
表2 谱图还原模型结果与光线追迹结果对比
中阶梯光栅光谱仪的工作范围覆盖190~600 nm,使用中阶梯光栅的第44~138色散级次,选取该级次范围内的边缘级次和中间级次作为对比级次,其中44,138级次为多项式拟合使用级次,且非拟合所用波长所在级次,46,91,135级次为非拟合级次。
在整个拟合过程中,选取第44,46,91,135,138级次自由光谱区内的上边缘波长、中间波长和下边缘波长,共计18个波长,进行理论位置追迹并与采用拟合模型计算所得的坐标位置进行对比,对追迹与拟合数据保留了小数点后5位,所有数据进行了四舍五入处理。
该中阶梯光栅光谱仪在设计过程中相邻级次间隔至少为一个像元,因此,相应的谱图还原模型误差需小于一个像元。从对比数据中可以看出,在X方向上,误差最大约为24 μm,在边缘级次44级的边缘波长处,该级次为拟合使用级次,造成较大误差的原因为该级次自由光谱区较大,所涉及波长拟合个数要比短波处相对多,但已满足使用要求。在Y方向上,各个级次的波长均与理论值吻合较好,具有较高的拟合精度。在整个谱图内该算法的坐标拟合误差小于一个像元,可以满足实际应用需求。
4.2 谱图还原算法实际对比实验
中阶梯光栅光谱仪的主要作用是获得所需波长或波段的光信号强度,辅助其所集成检测系统完成物质成分的定性和定量分析。因此,需要建立探测光束波长与强度的精确对应关系,即光谱标定。为验证所提出的基于多项式拟合的中阶梯光栅光谱仪谱图还原算法的准确性,分别采用该算法与传统基于公式归纳法的谱图还原算法对同一台中阶梯光栅光谱仪进行光谱标定,对比两种算法的标定结果。
光谱标定过程中,依据谱图还原算法将探测器接收光斑的位置坐标与其波长精确对应,将中阶梯光栅光谱仪特有的二维谱图还原成波长与强度的一维光谱数据。实验过程采用氩汞灯作为特征光源,在仪器工作波段即190~600 nm内,选取253.656,296.728,302.150,334.148,404.650,407.783,576.961,579.067 nm,共计8个能量较强的特征峰波长作为对比波长。通过所提出的基于多项式拟合的谱图还原算法与传统基于公式归纳法的谱图还原算法分别进行光谱标定,得到的波长数据对比如表3所示。

表3 两种谱图还原算法的光谱标定结果对比
由表3可知,基于多项式拟合的中阶梯光栅光谱仪谱图还原算法相较传统的公式归纳法,还原精度基本在一个水平,在可见光波段相对更高,在靠近紫外区域虽相对低,但还原精度基本小于仪器的光谱分辨率指标0.02 nm,可以满足实际应用要求。
采用公式归纳法需基于几何光学原理建立光束经过仪器内部每一光学元件后位置相对于接收表面的变化,从算法的构建到编程实现,过程复杂,尤其是对于内部组件较多的光学结构,应用难度较大。而采用多项式拟合的谱图还原算法,基于中阶梯光栅光谱仪采用组合分光元件分别在横纵两方向独立色散所形成的二维谱图特点,直接通过位置坐标拟合实现谱图还原标定,操作简单,通用性强。
5 结 论
本文设计了一种基于多项式拟合的中阶梯光栅光谱仪高精度谱图还原算法,通过级次间拟合的方式,只需追迹少量的光线即可获得整个谱段内波长的成像位置,该方法可实现快速、高精度的谱图还原模型建立。将研究结果应用于棱镜-光栅交叉结构的中阶梯光栅光谱仪中,验证了所建立模型的计算误差最大为0.023 92 mm,即所构建的谱图还原模型在整个像面内的坐标误差均小于一个像元。通过与传统谱图还原算法的光谱标定结果对比,标定精度基本持平,波长准确度优于仪器的光谱分辨率指标。该算法无需考虑中阶梯光栅光谱仪内部结构以及像差校正,只需关注光线在像面上的成像位置,模型建立具有很强的实用性和灵活性,不受限于复杂光路结构,适用于各种类型的中阶梯光栅光谱仪。

