Global classical solutions and asymptotic behaviors in chemotaxis systems with Logistic source on RN

HUANG Jinfeng,DU Wanjuan

(School of Mathematics and Information, China West Normal University, Nanchong, Sichuan 637009, China)

Abstract: This paper deals with the Cauchy problem of the parabolic-elliptic Keller-Segel chemotaxis model

where the parameters χ,a,b are positive constants,k>1 and N is a positive integer. First, it is shown that this system possesses the global existence and boundedness of the classical solution (u(x,t;u0),v(x,t;u0)) for the given initial function u0(x)=u(x,0;u0). Furthermore, we consider the asymptotic stability of the constant a constant C>0.

Key words:Keller-Segel system;logistic source;global classical solution;asymptotic behavior

1 Introduction

The motion of cells moving towards the higher concentration of a chemical signal is called chemotaxis. A well-known chemotaxis model was proposed by Keller and Segel in 1970 (see [1]). In recent 50 years, the original model has been modified by different authors to improve the applicability of the model (see[2]). To stimulate our study, we recall some related works concerning to the following system

(1.1)

whereuandvdenote the density of cells and the concentration of the chemical substance, respectively. Hereτ∈{0,1} andχ>0 is called the sensitivity of chemotactic response, the functionf(u) is used to model proliferation and death of cells.

(1.2)

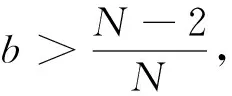
(1.3)

Since nonnegative initial function has practical significance, we first consider the global solutions of (1.3) for the given initial functionu0(x). If

u,v∈C(RN×[0,T))∩C2,1(RN×(0,T)) for (x,t)∈RN×(0,T)

and satisfies (1.3), we name a classical solution (u(x,t),v(x,t)) of (1.3) on [0,T). If

u≥0andv≥0 for all (x,t)∈RN×(0,T),

we say the solution (u(x,t),v(x,t)) of (1.3) is nonnegative on [0,T). Let us define

The main results of this paper can be stated as follows.

(1.4)

withsomeconstantC>0,thentheuniqueglobalclassicalsolution(u(x,t;u0),v(x,t;u0))of(1.3)withu(·,0;u0)=u0satisfies

(1.5)

2 Proof of Theorem 1.1

In this section, our goal is to prove Theorem 1.1.

ProofofTheorem1.1 Let (u,v) be the solution given by Lemma 2.1 defined on the maximal interval [0,Tmax(u0)). With the help of first and second equations of (1.3), we have

ut=Δu-χ▽·(u▽v)+u(a-buk)

=Δu-χ▽u▽v-χuΔv+au-buk+1

=Δu-χ▽u▽v-χu(v-u)+au-buk+1

≤Δu-χ▽u▽v+χu2+au-buk+1.

LetU(t,‖u0‖∞) be the solution of the following ODE

Sincek>1,U(t,‖u0‖∞)is globally bounded defined in time. Sinceu0≤U(0,‖u0‖∞), according to the comparison principle for parabolic equations, we have

u(x,t)≤U(t,‖u0‖∞) for allx∈RN,t≥0.

Clearly,u(x,t) is globally bounded defined in time, this is the end of the proof.

3 Proof of Theorem 1.2

Using the definitions of limsup and liminf, for any givenε>0 there isTε>0 such that

(3.1)

According to the comparison principle for elliptic equations, we derive that

(3.2)

Hence, combing (3.1) with (3.2), we obtain

(3.3)

As a matter of convenience to our proof of Theorem 1.2, we first present a well-known lemma [9, Lemma 4.1].

Lemma3.1Considertheordinarydifferentialequation

ut=u(m-nu),

(3.4)

wherem>0,n>0areconstants.Hereu(t;u0)isasolutionof(3.4),whereu(0;u0)=u0∈R.Thenforanyu0>0,

Lemma3.2Itfollowsfrom(3.1)and(3.3)that

(3.5)

Proof. Since (u,v) is a solutions of (1.3), with the help of first and second equations of (1.3), combing (3.1) with (3.3), we have

ut=Δu-χ▽u▽v+u(-χv+χu+a-buk)

(3.6)

Letw(t) be the solution of the following ODE

(3.7)

In view of (3.6) and (3.7), applying the comparison principle of parabolic equations, we have

u(x,t)≤w(t) ∀x∈RN,t≥Tε.

(3.8)

According to Lemma 3.1, we deduce that

(3.9)

By (3.8) and (3.9), it holds that

(3.10)

Lettingε→0in (3.10), we prove the first inequality in (3.5).

Similarly,

ut=Δu-χ▽u▽v+u(-χv+χu+a-buk)

(3.11)

In the following letv(t) be the solution of

(3.12)

Hence, by (3.11) and (3.12), and applying the comparison principle of parabolic equations, one can find

u(x,t)≥v(t) ∀x∈RN,t≥Tε.

(3.13)

Lemma 3.1 implies

(3.14)

By (3.13) and (3.14), we have

(3.15)

Lettingε→0 in (3.15), we also obtain the second inequality in (3.5). Given all this, Lemma 3.2 is proved.

Now we shall show the following lemma.

Lemma3.3 Suppose that

(3.16)

withsomeconstantC>0,thenonecanfind

(3.17)

Proof. Since (u,v) are solutions of (1.3), with the help of first and second equations of (1.3), we get

ut=Δu-χ▽u▽v-χuΔv+au-buk+1

=Δu-χ▽u▽v-χu(v-u)+au-buk+1

≥Δu-χ▽u▽v-χuv+au-buk+1.

From (3.2), we can find a positive constantC>0 such thatv≤C. Ifa>2χC,we see that

ut≥Δu-χ▽u▽v-χCu+au-buk+1

LetH(t) be the solution of the following ODE

Sincek>1,H(t) is globally bounded defined in time. Sinceu0(x)≥H(0), according to the comparison principle for parabolic equations, we obtain

u(x,t)≥H(t) for allx∈RN,t≥0.

(3.18)

Furthermore, Lemma 3.1 implies

(3.19)

By (3.18) and (3.19), we have

(3.20)

Lemma3.4When

(3.21)

itcomesfromLemma3.2that

Proof. Since

it is easy to find

which yeilds

(3.22)

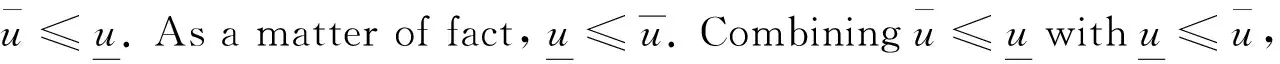
(3.23)

Then using Lemma 3.2 we obtain

(3.24)

Therefore, we follow from (3.24) that

(3.25)