ANA 误差下非参数回归模型中估计量的相合性
何其慧
考虑如下非参数回归模型:
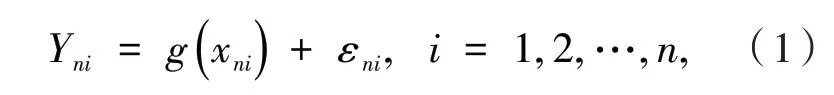
其中:xni为紧集A⊂Rp上的固定设计点列,g为A上待估的回归函数,εni,1 ≤i≤n,n≥1为随机误差.考虑如下关于g的线性加权估计:

其中:Wni(x) =Wni(x;xn1,xn2,…,xnn),i= 1,2,…,n为权函数.
上面的估计量(2)最早由Georgiev[1]提出.由于其广泛的适用性,很多学者都对此估计量进行了深入的研究,如文献[2-8].由于独立假设的不合理性,近些年来很多学者都将独立场合下经典的极限理论和统计大样本理论推广到各种相依情形.本文将在一类非常宽泛的相依结构——渐近负相协(ANA)误差下继续研究估计量(2)的相合性.ANA(或ρ--混合)随机变量的概念是由文献[9]提出的.
定义混合系数如下:

其中ℂ 是非降函数的集合.若混合系数
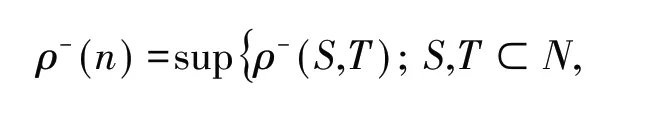
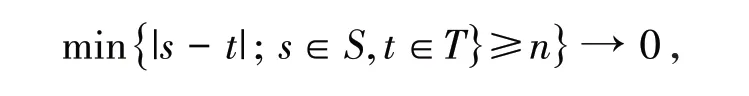
本文引用如下一些记号:C代表正的常数,在不同的地方可以取不同的值,I(A)为事件A的示性函数,[x]表示不超过x的最大整数,a+=aI(a≥0)且a-= -aI(a< 0).
1 预备知识
下面介绍关于随机控制的概念.
定 义1[9]若存在常数C,使得对所有的x≥0及n≥1,都有

则称随机变量序列{ }Xn,n≥1 被随机变量X随机控制.
为证明本文的主要结果,还需要下述几个重要引理.
引 理1[9]设随机变量{Xn,n≥1}为ANA的.若为单调非降(或非增)函数序列,那么仍为ANA 的,且其控制系数不大于ρ-(n).
引 理2[12]假设为均值是0 的ANA 随机序列且存在p≥2,使得则存在仅依赖于p及的常数C,使得
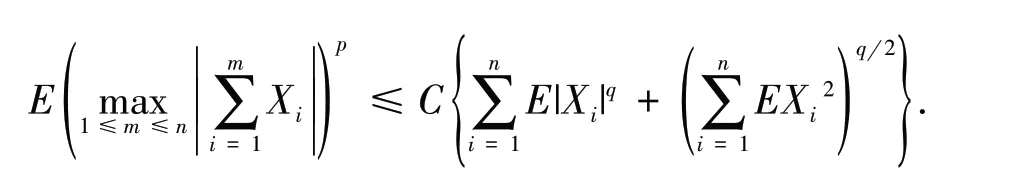
由引理2 及文献[13]中定理2.1 的方法,可得到如下关于ANA 随机变量的Marcinkiewicz-Zygmund 型矩不等式.
引 理3[13]假 设{Xn,n≥1}为均值是0 的ANA 随机序列且存在1 引 理4[14]假 设是被随机变量X随机控制的随机序列,则对任意的a> 0,b>0 及n≥1,都有 其中:C1和C2代表不同的正常数. 在给出主要结果之前,需要列举下列3 个基本条件: 基于以上条件,可以建立如下关于ANA误差下估计量(2)的完全相合性的结果. 定理 1 假设条件①~③成立 .为均值是0 的ANA 随机误差阵列且被随机变量ε随机控制,若存在s> 0,使得且 则对g(x)的所有连续点x与任意的δ> 0 都有 进而有 证明 类似文献[6]中(4.3)式的证明,可以由条件①~③推出 因此,由式(5)知只需证明对任意的δ> 0, 由引理1 可知{Xni,1≤i≤n,n≥1}仍然为ANA 随机变量阵列.因此式(6)可分解为 下面将证明I<∞及J<∞. 由条件①、E|ε|1+1/s<∞及引理4,可得 下面证明J<∞.首先证明当n→∞时, 事实上,由Eεni= 0,Wni(x) ≤n-s,以及引理4可得 因此,当n充分大时故由Markov 不 等 式、引 理2、Cr不等式及Jensen 不等式可得对p> max{2,2/s,1+1/s}, 由Cr不等式,定义1 及引理4 可知 由I<∞的证明可得 而对于J11,可将其分解为 同样由I<∞的证明可得此外由可得 最后来证明J2<∞.注意到由Cr不等式及引理4 可得 而若0 从而式(3)得证.式(4)可由式(3)及由Borel-Cantelli 引理立即得到. 注1:文献[6]在-混合误差下建立了估计量(2)的完全相合性的结果,而本文则是在较-混合更加宽泛的ANA 误差下建立的,因此具有更广泛的适用性.此外定理1 的证明和文献[6]的证明是有很大不同的,事实上,定理1 的证明要简单的多. 下面给出定理1 在最近邻估计中的应用.不 失 一 般 性,取A= [0,1],xni=i/n,1 ≤i≤n.对任意的x∈A,将|xn1-x|,|xn2-x|,…,|xnn-x|重新排序如下: 其中,若存在i 从而模型(1)中关于函数g的最近邻估计可定义如下: 基于以上论述,下面给出关于模型(1)中最近邻估计量的完全相合性的结果. 定理2 假设{εni,1≤i≤n,n≥1}为均值是0 的ANA 随机误差阵列且被随机变量ε随机控制. 若存在0 进而有 证明 由定理1 可知,只需验证W~ni(x)满足条件(H1)~(H3).由于g(x)在紧集A上连续,故在A上必有界,记为对 任 意的x∈A,由的定义可知 及∀a> 0,有 证明 由Cr不等式可得 故由式(5),为了证明式(8),下面只需证明 不失一般性,仍然假设Wni(x) ≥0,从而仍然为均值是0 的ANA 随机误差阵列.若1 而若r> 2,由引理2 可得 注2:文献[5]在误差为线性过程下建立了估计量(2)的矩相合性的结果.在其结果中要求存在r≥2,使得且而 定 理3 中 将r的 范 围 由r≥2 改进到r> 1. 本文主要利用关于ANA 序列的Rosenthal-型矩不等式,建立了ANA 误差下非参数回归模型中加权估计量的完全相合性,其结果推广改进了WANG 等人关于-混合误差下的相应结果.作为应用,还得到了ANA 误差下最近邻估计量的完全相合性.此外,利用ANA序列的Marcinkiewicz-Zygmund 型矩不等式,进一步得到了加权估计量的矩相合性,所得结果改进了胡舒合等人所得结果中的矩条件.
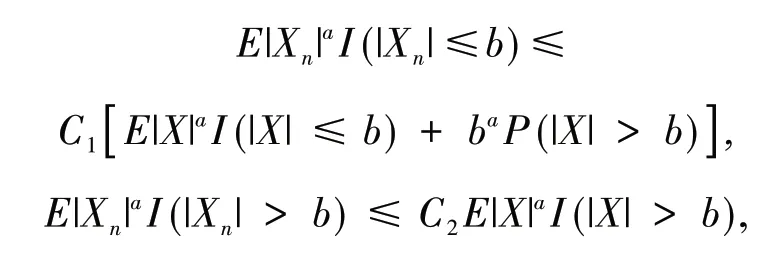
2 主要结果
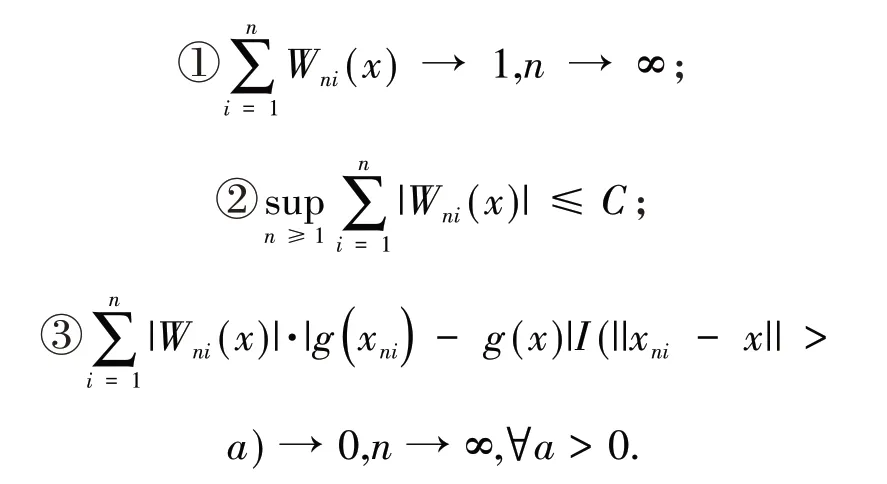
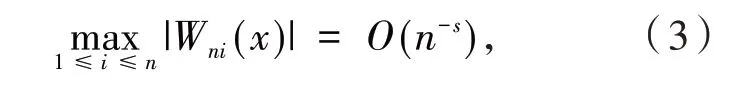

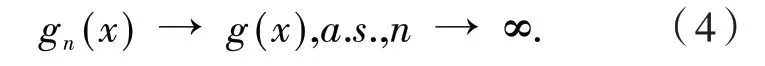
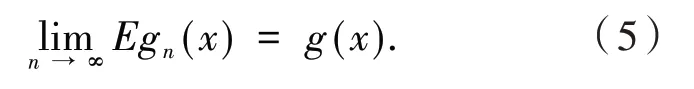



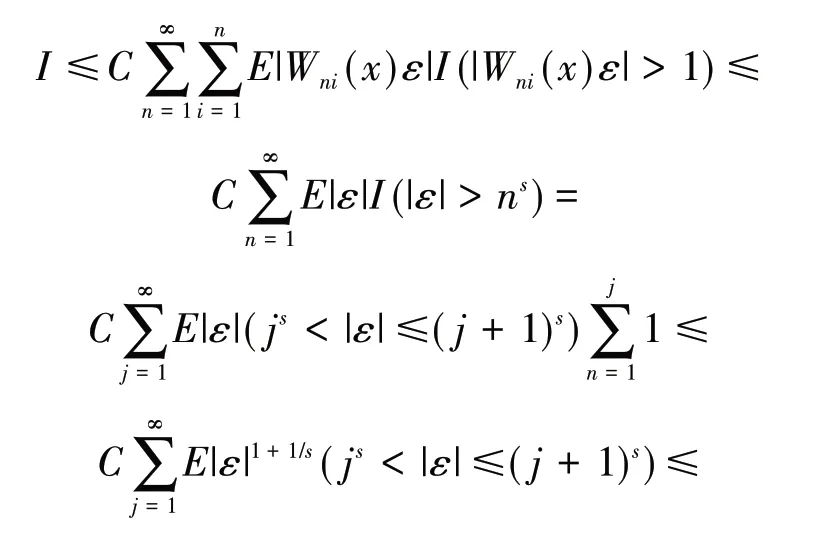
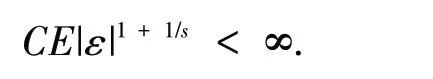


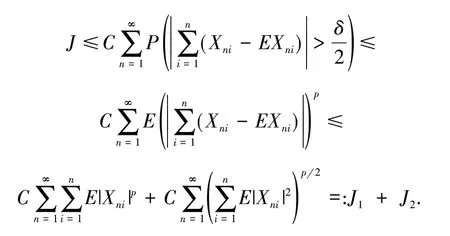
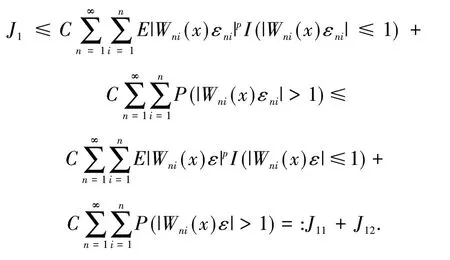

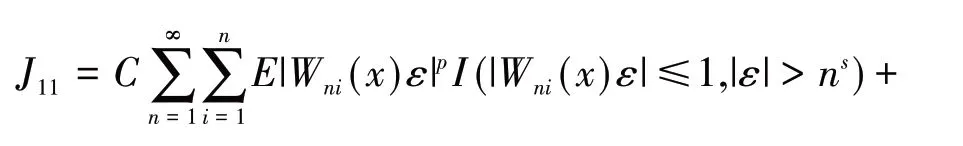


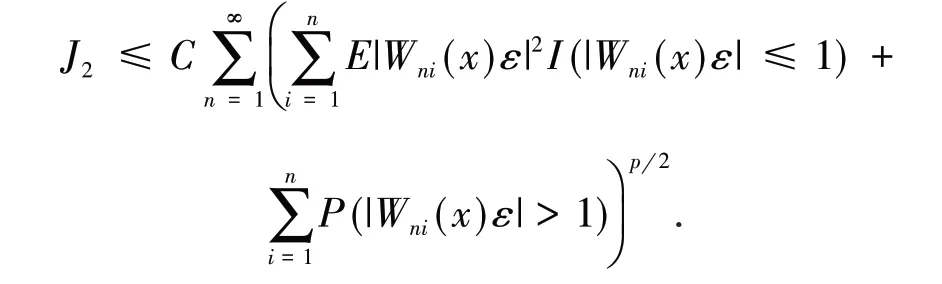
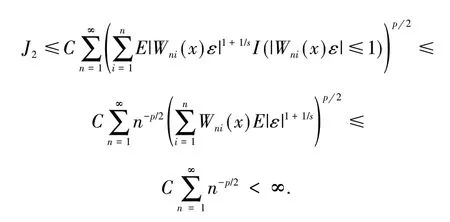
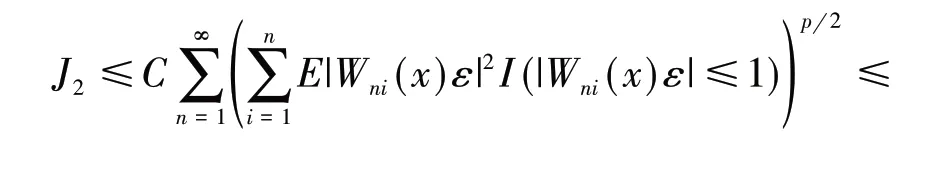
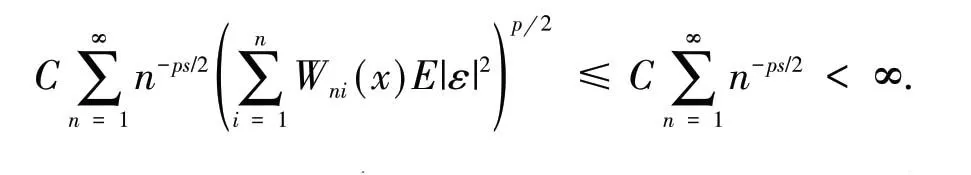
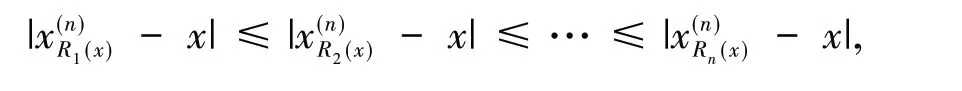
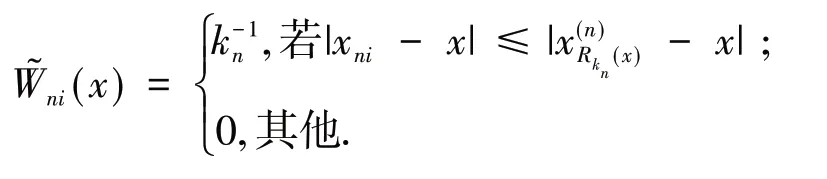

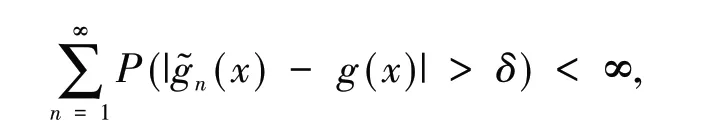
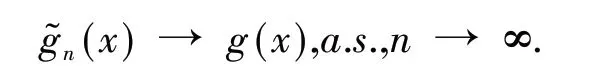

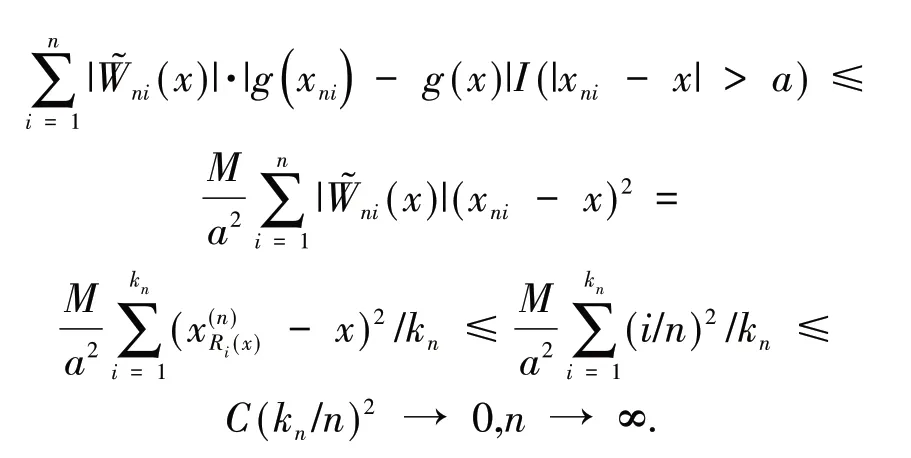

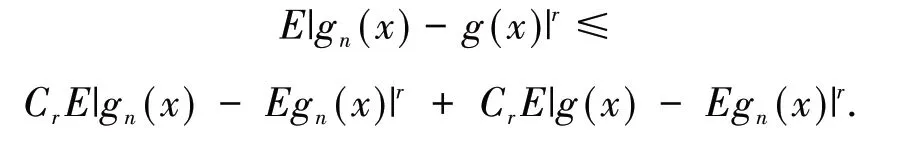
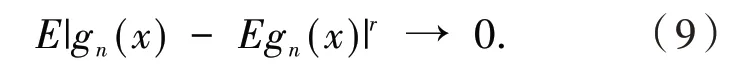
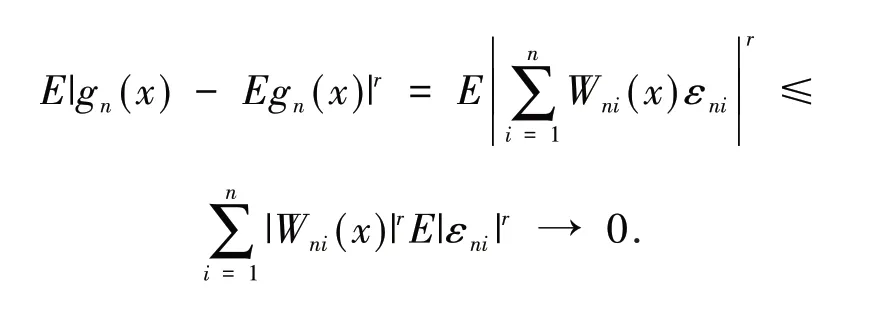
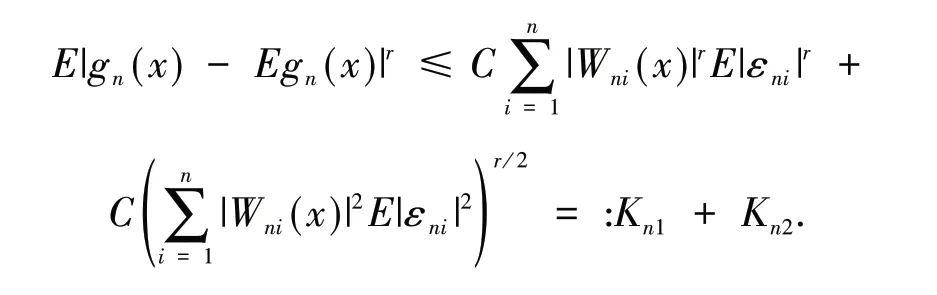
3 结语

