植根旋转模型,孕育核心素养*——由历史名题引发的探究与启示

广东省佛山市南海区南海实验中学(528200) 李林波

1 旋转模型的引出

法国数学家费马曾提出一个数学名题:在三角形所在平面内求一点,使该点到三角形三个顶点的距离之和最小,后人称此为费马点问题. 如图1,已知三角形∆ABC,求作一点P,使PA+PB+PC的值最小.

图1

图2

对学生而言,费马点问题是“熟悉的陌生人”,它涉及熟悉的三角形知识及距离最小的相关公理,而需要解决的却是陌生的三线之和最小. 学生一般的方法,如利用对称“化折为直”,或通过确定动点轨迹求最值等在这里都无从下手.

尽管费马点问题在历史上已被解决,但探索费马点过程所蕴含的数学价值并未随之消散. 如图2,费马点问题的一个解决方法是利用旋转三角形把到三顶点距离之和转化到两定点连线长. 这个解法非常巧妙,没经验的读者一时也难以想到,究其原因,是我们对几何变换产生的性质规律了解不深,未积累出相应的解题模型和解题方法.

初中的几何变换有全等变换(包括平移、轴对称和旋转)与相似变换,而三角形作为初中几何的基本组成部分,它的全等变换或相似变换往往成了解决几何问题的突破口. 对比平移与轴对称变换,旋转的变化更多,因为它涉及旋转中心、旋转角度和旋转方向这三个要素. 因此,我们有必要把三角形的旋转变换对边角产生的关系作进一步的探究.

2 旋转模型的认识

如图3, 我们把∆ABO绕点O旋转一个角度得到∆A′B′O, 连接AA′、BB′, 则得∆OAA′和∆OBB′为等腰三角形,且∆OAA′∽∆OBB′;如图4,∆ABO按一个比例放缩后再绕点O旋转一个角度得到∆A′B′O, 此时可得∆OAA′∽∆OBB′. 我们把图3、图4 称为旋转模型,其中图3 作的是全等变换,三角形变换前后形状、大小不变;图4作了相似变换,变换前后三角形形状不变,但大小改变了.

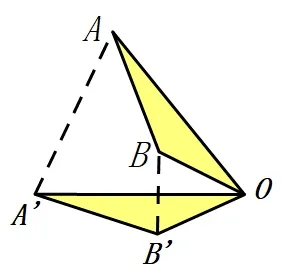
图3

图4

3 旋转模型的性质

如图5、图6,一个图形在平面内绕一点旋转,或按一个比例放缩后再绕一点旋转,连接两组对应点、旋转中心,可构造出图3、图4 的旋转模型. 因此,探究旋转变换对图形产生的几何关系往往归结到旋转模型去分析说明,以下是本人从一些角度探讨的部分几何关系.

图5

图6

3.1 当旋转中心为图形中的顶点时,对应边所在直线的夹角等于旋转角

如图6, ∆ABC绕点A逆时针旋转α(0° < α <180°,下同)得到∆AB′C′,则我们可类似图7 的构图方法证得对应边BC与B′C′所在直线的夹角等于α.

图6

图7

3.2 当旋转中心不是图形顶点,而是图形所在平面的任意点时,对应边所在直线的夹角依然等于旋转角,而且在保持旋转角和旋转方向不变的前提下,这些旋转图形之间是平移的关系

如图8,点O是平面上任意点,∆ABC绕点O逆时针旋转α得到∆A′B′C′,则对应边BC与B′C′所在直线的夹角等于α. 这点我们可以通过如图9 构造∆OBC和∆OB′C′来说明,显然∆OBC和∆OB′C′构成的旋转模型,旋转角为α,于是转化为第(1)条性质的情形来说明对应边BC与B′C′所在直线夹角等于旋转角α. 如图10,在其他两要素不变的前提下,改变旋转中心O的位置,∆ABC绕点O逆时针旋转α得到∆A′B′C′和∆A′′B′′C′′,联系平行四边形知识可推导出∆A′B′C′和∆A′′B′′C′′是平移的关系.

图8

3.3 当旋转中心、旋转角和旋转方向都不变时,把图形以旋转中心为位似中心同侧放缩,则这些放缩图形旋转后也是位似关系

图10

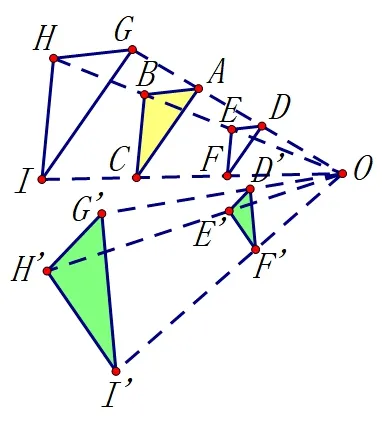
图11

如图11,∆ABC以O为位似中心同侧放缩得∆DEF和∆GHI, 再把∆DEF和∆GHI以O为旋转中心, 逆时针旋转α,所得∆D′E′F′和∆G′H′I′则是以旋转中心O为位似中心,位似比为放缩比之比的位似图形. 这点读者可以结合旋转性质与位似定义加以体会理解.

4 旋转模型的运用

一个几何问题在解决时感觉困难,往往在于对条件、图形以及所求的转化上. 如图12,费马点问题的难处是如何把到P到三定点A、B、C的距离之和转化为两定点M、N之间的连线长.

图12

图13

如图13, 我们把∆APB绕点A往外旋转60°得∆AP′B′,则等腰∆APP′为等边三角形,故有PA+PB+PC=PP′+P′B′+PC, 其中B′是定点, 从而把到三定点的距离之和转化为两定点之间的连线长,这是解决费马点问题的突破口. 由此我们看到了旋转角度对边的转化产生了奇妙的影响,如图14,若∆APB绕点A往外旋转90°得∆AP′B′,则PB+PA=PB+PP′,这样可为边的不同加权之和提供解决思路.

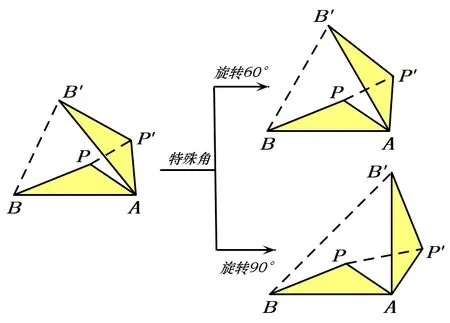
图14

问题1如图15, 已知正方形ABCD, ∠EBF=∠EDF=45°,连接AF、CE,求证:AF//CE.

图15

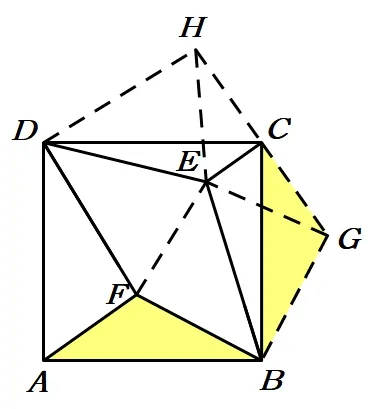
图16

分析因为AB=CB,联想到旋转模型,我们把∆ABF绕点B旋转到∆CBG,如图16,连接有关线段,进一步得出∆BEF∆BEG,同理把∆ADF绕点D旋转到∆CDH,也得出∆DEF∆DEH. 有兴趣的读者可以循着思路往下探究出结果. 在这里我们发现旋转模型在一定的条件下可以发生连锁反应,如上述分析中的∆BEF∆BEG,究其原因,是添加了条件∠EBF=45°,它为旋转角度的一半,如图17,我们称之为半角模型,像这样改变条件引起连锁反应的例子还有很多,这里不逐一列举,细心的读者可以在平时留意体会.

图17

问题2如图18 所示,二次函数y=ax2+bx+c的图象经过A(4,0),B(−1,0),C(0,−2)三点,

(1)求出二次函数的表达式;

(2)若连接BC,把∆BOC绕平面内某点R逆时针旋转90°得到∆B′O′C′, 点B、O、C的对应点B′、O′、C′, 若∆B′O′C′的两个顶点恰好落在抛物线上,那么我们就称点R为“旋转点”,请直接写出满足条件的点B′的坐标.

图18

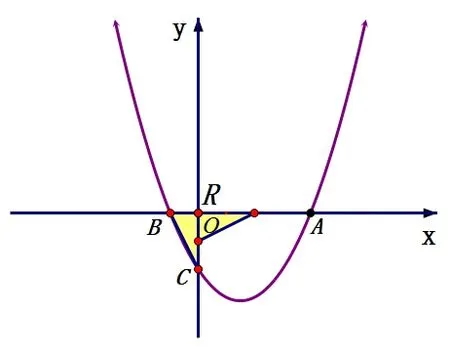
图19

分析问题的第(2)问涉及了旋转模型的延拓——旋转中心是平面内的任意点,如图19,我们把旋转中心R取在O上,得到∆BOC逆时针旋转90°的旋转后的图形,由旋转模型的第(2)条性质可知,R取其他位置时,实质为该图形平移的结果,从而确定∆B′O′C′的摆放方式,然后分类讨论解决,如图20、图21.

图20

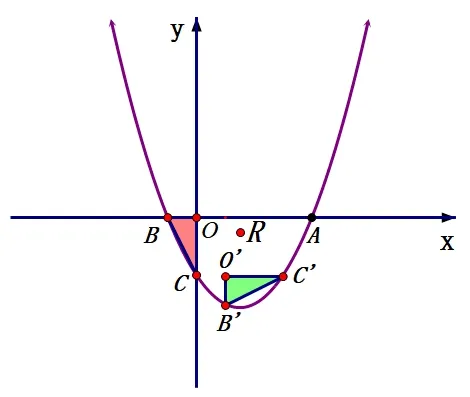
图21

问题3如图22,⊙A的半径为1,点A坐标为,点P是⊙A上的动点,点B与点P关于原点中心对称,且∆PBC是等边三角形,当P在⊙A上的运动时,点C围成的图形的面积是____.

分析连接CO,我们发现对于点C 形成的图形,如图23,按旋转模型的性质(3),我们可以分两步理解:(1)先以点O为位似中心,在同侧把OP放大倍得OC′,这等同于在同侧把⊙A放大为原来的倍得⊙A′;(2)再把C′绕点O逆时针旋转90°得点C,这等同于对⊙A′作全等变换,所以点C形成的图形是⊙A′′.

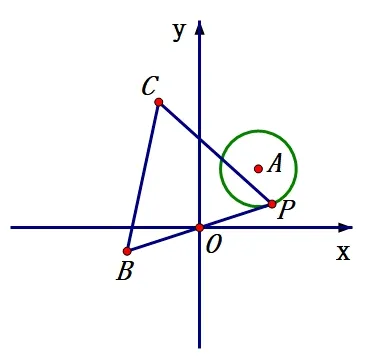
图22

图23

5 旋转模型的启示

(1)意义深刻的数学问题从来都不是一找出答案就完事,历史上还有很多像费马点问题那样数学名题值得我们可以重新思考,变式拓展,并把前辈所发现的解答纳入到我们学习体系和应用当中. 通过对这些数学名题的探究学习,学生能加强图形的辨识能力,提高几何证明的质量,同时也领略了数学文化的意蕴,推动自身数学素养的形成.

(2)数学教育家波利亚在《怎样解题》里指出:面对一个问题你无从下手时,你可以找一个辅助的问题,希望通过它帮助我们去解决原问题,我们可以用辅助问题的结果,也可以利用辅助问题的方法[1]. 旋转模型正是费马点问题的辅助问题,如果我们把旋转模型研究透彻了,遇到类似问题时自然想着通过旋转把分散的条件集中起来,从而达到解决问题的效果,这是获取知识与方法的有效途径.

(3)如果一个辅助问题能抽象地、概括地表征所研究对象的主要特征及其内在联系,具有普遍性、实用性,那它就成了常用的基本模型,一个解题模型. 这样的模型携带着思路片段,为整个几何问题的思路提供拼图的作用,形成解答方案. 旋转模型可以作为一个基本模型,它的建立与应用体现了数学的模型思想以及化归思想,其中模型思想是新课标下10 个核心概念中唯一一个以思想指称的概念,它是数学基本思想之一[2]. 当改变一些条件时,旋转模型又衍生出更多规律性更强的解题模型. 其实,不仅旋转模型如此,数学的很多模型也是如此,这需要我们平时注重总结归纳.