5G系统中基于三阶相关的同步算法及FPGA实现

李贵勇，张翰卿，王永航

(重庆邮电大学 通信与信息工程学院，重庆 400065)

0 引 言

5G用户设备(User Equipment，UE)开机后的第一步是小区搜索过程[1]。UE通过检测主同步信号(Primary Synchronization Signal，PSS)和辅同步信号(Secondary Synchronization Signal，SSS)得到物理小区标识(Physical Cell Identifier，PCI)和时频同步，并在进行信号均衡后解析物理广播信道(Physical Broadcast Channel，PBCH)，获得主系统信息(Master Information Block，MIB)。

检测同步信号的过程，尤其是同步点的准确与否对于性能的影响极大。循环前缀(Cyclic Prefix，CP)技术允许同步点可以有一定程度的向前偏移，但是其造成的相位偏移在后续过程中很难通过算法来弥补，对于接下来的信道处理过程有很大影响。而同步点向后偏移造成的数据丢失则完全无法消除。

因此，本文将着眼于检测同步点的性能。文献[2]介绍了使用最广泛的时域互相关算法，将接收时域信号与本地生成的PSS时域序列进行相关；文献[3]提出了一种时域自相关算法，利用PSS时域序列的共轭对称性计算同步点；文献[4-5]提出了一种分段互相关算法，将接收信号分段相关，以降低频偏累加造成的影响；文献[6]利用现场可编程门阵列(Field Programmable Gate Array，FPGA)的并行策略实现了下行同步算法。

本文基于m序列的三阶自相关特性，提出了一种新型的定时同步检测FPGA算法，有望在低信噪比环境下提高同步过程中同步点的准确性，并通过Matlab和SE14.7等软件搭建了仿真链路，以验证算法的复杂度与可行性。

1 5G下行同步过程

下行同步是小区搜索过程的第一步。UE按照全球同步栅格(Global Synchronization Channel Number，GSCN)对应的频段搜索同步广播块(Synchronization Signal/PBCH Block，SSB)中的PSS和SSS。

图1所示为5G系统下行同步过程，下行同步首先检测PSS。UE通过对接收到的信号采用降采样等方法进行处理，粗略地检测PSS存在的大概位置，此过程称为粗同步过程，检测的PSS粗略位置称为粗同步点。以粗同步点为基准，检测出准确的PSS时域序列位置的过程称为精同步过程，得到的PSS时域序列起始点称为精同步点[7]。

图1 5G系统下行同步过程

此外，UE在与基站建立连接后，由于时钟精确度和信号处理时延等问题，下行同步过程中建立的同步可能会逐渐偏离正确的同步点。为此，UE需要每隔一段时间重新计算同步点，此过程称为同步跟踪过程。

不同于4G中使用的Zadoff-Chu(ZC)序列，5G系统中PSS使用m序列，原因在于在存在时偏和频偏的情况下，ZC序列的相关函数存在较大的旁瓣，会影响检测性能[8]。令一个m序列为x(i)，则其三阶自相关函数为

式中：Cm为三阶相关值；i为离散序列相位；L为离散序列长度；p和q均为离散序列相对相位[9-10]。

根据m序列的移位相加特性，存在p和q，使得对任意i，有x(i-p)x(i+q)=x(i)，则根据m序列的性质，此时序列的三阶相关函数Cm出现峰值Cm(p,q)=1。对于其他的i、p和q组合，有x(i-p)x(i+q)≠x(i)，此时Cm(p,q)=-1/L，即m序列的三阶相关函数为

对于5G系统中PSS使用的m序列，其三阶相关函数峰值位置如表1所示。

表1 5G PSS三阶相关函数峰值位置

2 基于PSS三阶相关特性的同步算法

传统的PSS同步算法有时域互相关和时域自相关算法。

令接收信号为a(t)+n(t)，t为模拟信号相位，a(t)为有用信号，在本文中特指时域同步序列，n(t)为白噪声。若使用互相关方法，本地生成a(t)信号，并与接收信号进行互相关，则互相关值为

式中：v为未知相位，进行滑动相关时会变化，乘法代表序列相关运算。当n(t)的幅度较大时，有用部分a(t+v)a(t)可能会淹没在干扰部分a(t+v)n(t)中，造成性能损失。由此可知，互相关算法的抗干扰性能较差。

时域自相关算法是将当前接收信号与一个SSB检测周期后的接收信号进行相关，如果出现相关峰值，则认为该位置为PSS。此算法中若接收噪声为理想白噪声，则认为两个时刻的噪声没有相关性，相关值受噪声影响小。故自相关算法比互相关算法具有更加优秀的抗干扰性能。

虽然时域自相关算法理论上可行，但该算法需要储存一个SSB检测周期内的所有数据(文献[11]规定，如果UE没有配置，默认检测周期为20 ms)，所需空间资源极大，并且SSS与PSS有同样的自相关峰值特性，算法无法确定此位置究竟是PSS还是SSS。

本文基于PSS使用的m序列的三阶相关性质，提出一种可在精同步过程和同步跟踪过程中使用的新型同步算法。

对接收信号进行三阶相关，其相关值为

由于n(t)为白噪声，我们认为n(t)、n(t-p)和n(t+q)之间没有相关性，或相关性极小。a(t)为m序列，根据m序列的性质a(t)a(t+v)当且仅当v=0时有极大值，故在理想情况下式(4)仅剩下有用部分a(t)a(t-p)a(t+q)，相比于式(3)，有用部分的抗干扰性能更强。当然实际噪声不是理想白噪声，当噪声幅值足够大时，依旧会影响到有用部分的检测。

同时，三阶相关计算不需要其他时刻的信号。因此，此方法既可以使用自相关抵抗白噪声的干扰，又避免了时域自相关需要消耗大量空间和时间资源的问题。

算法具体流程如下：

令一段接收信号为s(t)，已经进行降采样使得一个正交频分复用(Orthogonal Frequency Division Multiplexing，OFDM)符号中采样点数为2 048点，并且已经下变频使得PSS所在的频域位置位于接收信号中频。

步骤1：假设粗同步过程计算出的同步点为s(v)，v为粗同步点在接收序列中的位置，计算粗同步点时的精确度为±16点。则UE认为s(v-15)、s(v-14)、…、s(v+16)中存在精同步点。

取[s(v-15)、s(v-14)、…、s(v+2 032)]、[s(v-14)、s(v-13)、…、s(v+2 033)]、…、[s(v+16)、s(v+17)、…、s(v+2 063)]这32段序列，分别作快速傅里叶变换(Fast Fourier Transform，FFT)，得到32组2048点频域序列。

步骤2：分别从这32组序列中取PSS所在位置的127点:

式中：PSSk为从频域序列中取得的32组PSS；wk(n)为步骤1中得到的32组频域序列。

步骤3：对这些序列进行三阶相关，得到

式中，Ck(p,q)为序列的三阶相关函数。

PSS三阶相关的峰值位置如表1所示。这里任取一理论峰值位置，如(p=3,q=4)处，则认为这32个相关值中的最大值Ck(3,4)对应的PSSk即为准确的PSS，其对应时域序列的起始点即为精确的定时同步点。

上述过程针对下行精同步过程，如果应用在同步跟踪过程中，只需要将步骤1中的粗同步点替换成现有的同步点即可。

3 仿真验证

使用Matlab软件搭建仿真链路。首先测试精同步过程中算法的性能。信道模型使用加性高斯白噪声(Additive White Gaussian Noise，AWGN)信道。令一个OFDM符号采样点数为2 048， PSS占据频域中心的127个点。粗同步过程的精确度为±16点，具体仿真参数配置,如表2所示。

表2 精同步过程仿真参数配置

作为对比，仿真还测试了文献[2]中提供的传统时域互相关算法和文献[3]中提供的基于CP共轭对称性的精同步算法。每种算法仿真1 000次，记录检测出正确同步点的次数并计算正确率。图2所示为3种算法在不同信噪比下正确率的对比。

图2 下行同步算法检测同步点的正确率

由图可知，如第2节所述，传统时域互相关算法在抗噪声方面能力有限，当信噪比下降至2 dB左右时，时域互相关算法已经无法保证100%的正确率；信噪比继续下降至2 dB左右时，时域互相关算法开始出现检测错误的情况，而基于CP共轭对称性的精同步算法和基于三阶相关的算法仍然保持着100%的正确率；当信噪比低至-7 dB后，三阶相关算法检测正确率相比时域互相关算法高出32%，比基于CP共轭对称性的精同步算法的正确率高出27%。

接下来测试算法在同步跟踪时的性能，信道和帧结构参数配置与精同步过程相同。如果信号接收模块的时钟精度足够高，则跟踪算法只需要1帧或两帧运行一次，就可以保证每次同步点的偏移不会很多。仿真中设置最大偏移量为5个点，即算法只计算当前同步点左右各5个点的相关值，而不是精同步过程中的左右各16个点。

作为对比，仿真测试了时域互相关算法和文献[12]提出的基于参考信号时域信道脉冲响应的同步跟踪算法，该算法用参考信号信道脉冲响应的幅值进行定时同步。图3所示为3种算法检测正确率的对比。

图3 同步跟踪算法检测同步点的正确率

三阶相关算法在同步跟踪过程中的性能与下行同步过程类似。而时域互相关算法由于限制了同步点的偏移量，检测正确的概率略有提高，但在低信噪比环境下仍然性能不佳。参考信号的发送功率一般比同步信号的发送功率高，所以基于参考信号时域信道脉冲响应的同步跟踪算法在3种算法中性能最好。当信噪比降低至-7 dB时，三阶相关算法检测正确率相比基于参考信号的算法低2%。

4 FPGA实现

本文使用ISE14.7软件编写了Verilog代码。采用xc7vx690t-1ffg1158作为FPGA芯片。FFT和乘法器模块均使用ISE14.7软件自带的ip核。图4所示为顶层寄存器转换级电路图。图中，Rx_data_r为输入的接收信号；Acc_syn_clk为时钟；adder_number为粗同步过程精确度；MAU_1_path_start为相关模块开始标志；Rst_n为复位信号；fft_2 048为2 048点FFT模块；MAU为相关计算模块；Acc_syn_cmp为相关值比较模块。

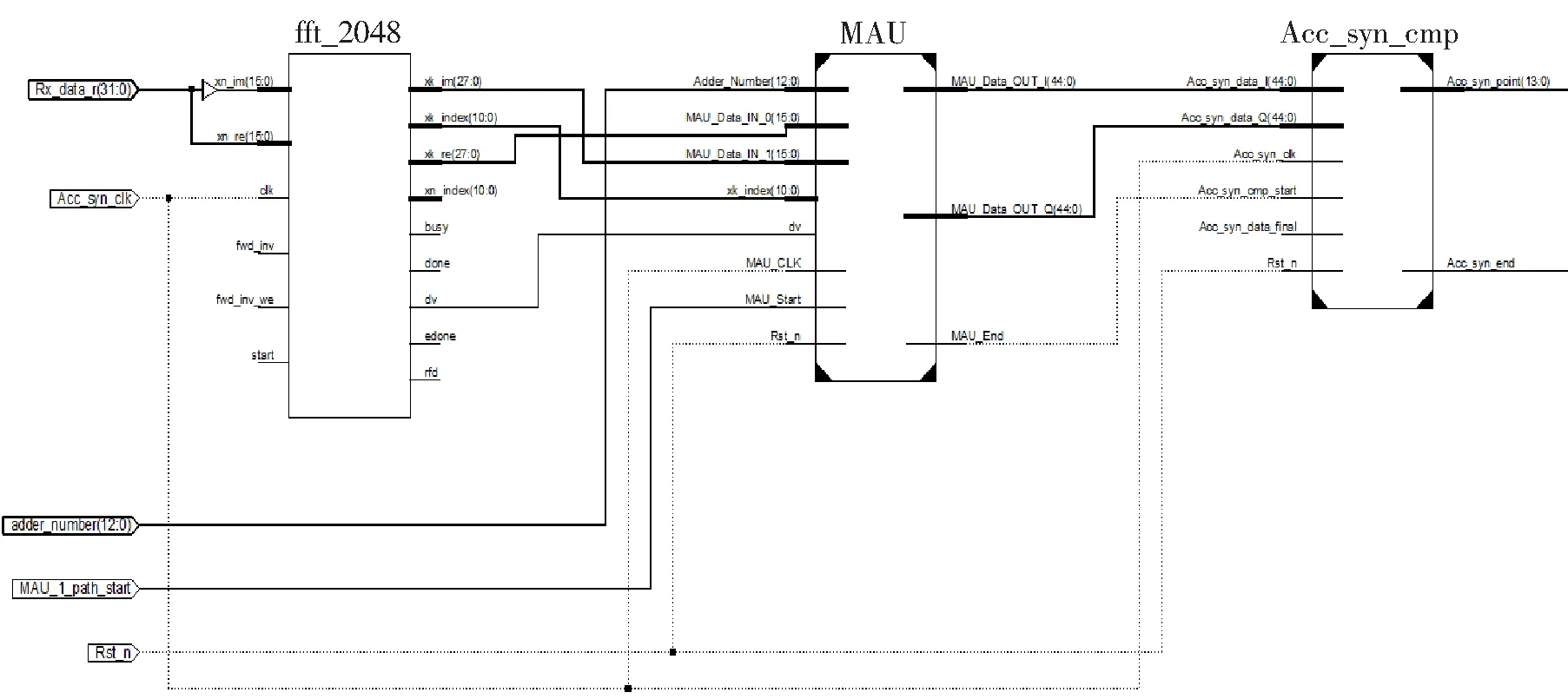
图4 FPGA代码寄存器转换级电路图

精同步过程开始后，分别将32组接收信号送至FFT模块进行时频域转换，然后将频域信号送至MAU模块进行三阶相关，最后将相关值送入Acc_syn_cmp模块进行比较，返回相关值最大的同步点为精同步点。

使用Matlab软件粗同步后的数据作为模块输入，验证FPGA算法。图5所示为FPGA代码和Matlab软件代码运行正确率比较。由于FPGA使用的定点数相比于Matlab软件使用的浮点数损失了小数部分的精度，故偶尔会存在Matlab代码检测正确而FPGA代码检测错误的情况，但整体上两者性能相同。

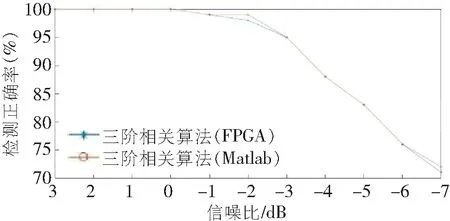
图5 软硬件代码性能比较

表3所示为三阶相关算法使用FPGA实现时占用的硬件资源。本算法的实现除了最基本的信号存储之外，需要1个FFT模块和1个127点相关模块，复数乘法1次需要4次乘法，则127点相关可以使用128×4/N个乘法器，其中N为正整数，可以根据需要调整。本文使用4个乘法器，另外还有两个乘法器实现复数求模，共6个乘法器。

表3 算法占用FPGA资源

表4所示为三阶相关算法和其他算法需要的模块数目比较。

表4 各种算法使用模块数

考虑到FPGA的模块复用机制，下行同步除了检测PSS还需要检测SSS，而检测SSS的过程一般在频域进行[13]，同步跟踪过程运行时信号已经从时域变换为频域，所以无论如何都需要1个FFT模块。这个模块考虑到，三阶相关算法、时域互相关算法和基于CP的精同步算法的资源消耗仅在于相关模块使用的乘法器数量。但基于参考信号的跟踪算法仍然需要额外的快速傅里叶逆变换(Inverse Fast Fourier Transform, ITTF)模块。

时间资源上，FFT所需时钟周期取决于设置，以本文配置的Pipelined, Streaming I/O、2 048点FFT为例，这种配置下，一次FFT需要6 265个时钟周期。相关过程需要的时钟周期取决于乘法器的数量，本文使用4个乘法器，则相关过程需要128个时钟周期，本文的算法需要204 576个时钟周期。

文献[11]规定SSB最低发送周期为5 ms，即理论上精同步过程和同步跟踪过程最快也要5 ms才运行一次，实际项目中假设同步模块的时钟频率为153.6 MHz (30.72 MHz×4), 5 ms总共有768 000个时钟，远远高于算法运行时间，故算法的时间复杂度是可以接受的。

实际情况中，按照5G系统的流程，下行同步过程只要正确检测出PCI即停止运行，不再需要运行算法。同步跟踪过程也不需要每5 ms运行一次同步算法，每1帧或两帧运行一次算法即可保持良好的同步性能。算法时间复杂度的影响将进一步减少。

5 结束语

本文根据m序列的三阶相关特性，提出了一种基于三阶相关的定时同步算法。仿真结果表明，相比于传统的下行精同步算法，三阶相关的定时同步算法可以在不使用更多空间资源的同时，具有良好的抗白噪声性能，而在实际应用中算法时间消耗的提升可以忽略。当信噪比下降至-7 dB时，三阶相关的定时同步算法与传统下行精同步算法相比，检测同步点的准确率提高了20%～30%。而在同步跟踪过程中，本算法的性能相比使用参考信号的算法低5%以内，但使用资源方面少用了1个IFFT模块。

但是三阶相关同步算法是精同步算法，当其应用在下行同步过程中时，非常依赖粗同步算法的性能。如果粗同步算法无法定位到准确同步点附近，UE在同步失败后会反复运行下行同步过程，此时本算法时间消耗的增加可能会导致整体同步过程时间延长。