形变微分算子代数的Poisson代数结构

高寿兰, 吴祺伟,2, 郑姝敏

(1. 湖州师范学院 理学院, 浙江 湖州 313000; 2. 上海大学 数学系, 上海 200444)

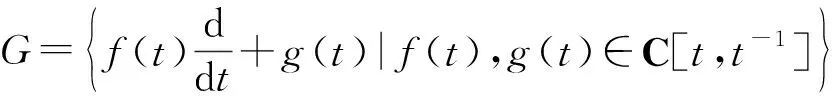
微分算子代数G(也是W(a,b)代数当a=b=0的情形[3])的结构和表示在近三十年来得到了广泛的研究[3-6].G的泛中心扩张[4]即为扭Heisenberg-Virasoro 代数,与曲线的模空间有密切联系,其结构和表示得到了深入的研究[3,7-11].

Fuchs[5]、Roger等[6]给出了G的一个2-上循环φ:G×G→G,定义如下:

由此诱导了形变李代数L=⊕m∈ZCLm⊕m∈ZCIm,满足如下关系式:

Gao等[12]对L的结构性质和Verma模的不可约性进行了刻画,其结构性质与G的结构性质有很大的不同[3,12].

全文中,Z表示整数集,C表示复数域,所有的线性空间都定义在C上.

定义1[17]在域F中,Poisson代数(A,*,[-,-])是一个线性空间A,同时具有代数乘法*和李代数乘法[-,-],且满足如下Leibniz法则:

[z,x*y]=[z,x]*y+x*[z,y]

∀x,y,z∈A

如果乘法*满足结合律,则称Poisson代数是结合的; 如果乘法*满足交换律,则称Poisson代数是交换的.

证明1) 设L0*L0=∑aiLi+∑bjIj+μ0C.由[L0,L0*L0]=[L0,L0]*L0+L0*[L0,L0],可得[L0,L0*L0]=0. 于是,有

从而iai=0,jbj=0,则当i≠0,j≠0时,ai=0,bj=0.故

L0*L0=a0L0+b0I0+μ0C

(1)

2) 设L0*I0=∑ciLi+∑djIj+ν0C.利用等式[L0,L0*I0]=[L0,L0]*I0+L0*[L0,I0],即[L0,L0*I0]=0,可得

类似于1)的讨论,可得

L0*I0=c0L0+d0I0+ν0C

(2)

3) 设L0*In=∑cniLni+∑dnjInj+νnC,n≠0.由[L0,L0*In]=[L0,L0]*In+L0*[L0,In],即[L0,L0*In]=-nL0*In,可得

即

显然

由式(3)知,当ni≠n时,cni=0.式(4)变为

ncnIn+∑(nj-n)dnjInj=0

(5)

在式(5)中取ni=n,得ncn=0.由于n≠0,所以

cn=0

于是,式(5)变为∑(nj-n)dnjInj=0. 从而(nj-n)dnj=0. 则当nj≠n时,dnj=0.因此

L0*In=dnInn≠0

(6)

4) 设L0*Ln=∑aniLni+∑bnjInj+μnC,n≠0.由[L0,L0*Ln]=[L0,L0]*Ln+L0*[L0,Ln],即[L0,L0*Ln]=-nL0*Ln-nL0*In,可得

从而

由式(7)知,当ni≠n时,ani=0.于是,式(8)变为

nanIn+∑(nj-n)bnjInj-ndnIn=0

(9)

在式(9)中,取nj=n,得nan-ndn=0. 由于n≠0,所以

dn=ann≠0

于是,式(6)变为

L0*In=anInn≠0

(10)

同时,式(9)变为∑(nj-n)bnjInj=0. 从而(nj-n)bnj=0,则当nj≠n时,bnj=0.因此,

L0*Ln=anLn+bnIn,n≠0

(11)

5) 设I0*I0=∑eiLi+∑fjIj+ω0C. 由[L0,I0*I0]=[L0,I0]*I0+I0*[L0,I0],即[L0,I0*I0]=0,可得

显然,iei=0,jfj=0.故当i≠0,j≠0时,ei=fi=0.因此,有

I0*I0=e0L0+f0I0+ω0C

再由[L1,I0*I0]=[L1,I0]*I0+I0*[L1,I0],即[L1,I0*I0]=0,得e0(L1+I1)=0,则e0=0. 故

I0*I0=f0I0+ω0C

(12)

6) 设I0*In=∑eniLni+∑fnjInj+ωnC,n≠0.由[L0,I0*In]=[L0,I0]*In+I0*[L0,In],即[L0,I0*In]=I0*[L0,In]=-nI0*In,可得

显然,ωn=0,n≠0.

类似于3)的讨论,可推出

I0*In=fnIn,n≠0

结合式(12),有

I0*In=fnIn+δn,0ω0C,n∈Z

(13)

7) 对任意m∈Z,由[Lm,I0*I1]=[Lm,I0]*I1+I0*[Lm,I1],可得

[Lm,I0*I1]=I0*[Lm,I1]=-I0*Im+1

利用式(13),得

f1Im+1=fm+1Im+1+δm+1,0ω0C

(14)

于是,f1Im+1=fm+1Im+1,则fm+1=f1. 显然,对任意的m∈Z,都有fm=f1. 在式(14)中,取m=-1,得ω0=0.因此

I0*In=f1Inn∈Z

(15)

8) 设n≠0,由[In,L0*I0]=[In,L0]*I0+L0*[In,I0],可得[In,L0*I0]=[In,L0]*I0,根据式(2),有nc0In=nIn*I0.故

In*I0=c0Inn≠0

(16)

9) 设n≠0,根据[Im,L0*In]=[Im,L0]*In+L0*[Im,In], 利用式(10),得mIm*In=0.故

Im*In=0,m≠0,n≠0

(17)

10) 由[Lm,L0*I0]=[Lm,L0]*I0+L0*[Lm,I0],可得[Lm,L0*I0]=[Lm,L0]*I0.当m≠0时,利用式(2)与式(16)可得,mc0(Lm+Im)=mLm*I0+mc0Im. 因此

Lm*I0=c0Lmm≠0

(18)

11) 由[I1,L-1*I0]=[I1,L-1]*I0+L-1*[I1,I0]及式(18),可得I0*I0=c0I0.再由式(15)知:

c0=f1

因此,综合式(15)与式(16),可得

In*I0=I0*In=c0Inn∈Z

(19)

12) 设n≠0,由[In,L0*L0]=[In,L0]*L0+L0*[In,L0]及式(1,10)得

In*L0=(a0-an)Inn≠0

(20)

13) 设n≠0,[Ln,L0*L0]=[Ln,L0]*L0+L0*[Ln,L0]及式(1，10，20),可得

na0Ln+na0In=n(Ln*L0+L0*Ln)+na0In

于是,有Ln*L0+L0*Ln=a0Ln.结合式(11),得

Ln*L0=(a0-an)Ln-bnInn≠0

(21)

14) 设n≠0,由[Im,L0*Ln]=[Im,L0]*Ln+L0*[Im,Ln]及式(11),可得

anIm+n=Im*Ln+L0*Im+n,m≠0,n≠0

(22)

若m=-n≠0,则Im*L-m=a-mI0-L0*I0.利用式(2),可得

Im*L-m=-c0L0+(a-m-d0)I0-ν0C,m≠0

(23)

若m+n≠0,将式(10)代入式(22),可得

Im*Ln=(an-am+n)Im+nm,n,m+n≠0

(24)

15) 通过[I1,I-1*L1]=[I1,I-1]*L1+I-1*[I1,L1]及式(17,23),可得-c0I1=I-1*I2=0.因此,

c0=0

(25)

从而式(2,18,19,23)变为

(30)

从而

由式(31)知:

gni=0ni≠n

这样,式(32)变为

ngnIn+∑(nj-n)hnjInj=0

(33)

在式(33)中,取nj=n,有ngnIn=0.由于n≠0,所以

gn=0,n≠0

于是,式(33)变为∑(nj-n)hnjInj=0. 从而(nj-n)hnj=0,则有

hnj=0nj≠n

因此,

I0*Ln=hnInn≠0

(34)

18) 由[Lm,I0*L0]=[Lm,I0]*L0+I0*[Lm,L0],得[Lm,I0*L0]=I0*[Lm,L0].根据式(28,30,34),有

g0Lm+(g0-hm)Im=0m≠0

于是,

g0=0

进而,对任意的m≠0都有hm=g0=0.于是,式(30)与式(34)可合并为

(35)

19) 设n≠0,由[Ln,In*L-n]=[Ln,In]*L-n+In*[Ln,L-n]及式(20,24,28,29),可得

(36)

特别地,当n=1时,有

a-1+a1=2a0

(37)

20) 设n≠0,m≠0,由[Im,Ln*L0]=[Im,Ln]*L0+Ln*[Im,L0]及式(21),可得

(a0-an)Im+n=Im+n*L0+Ln*Im

m≠0,n≠0

(38)

若m=-n≠0,则Ln*I-n=-I0*L0+(a0-an)I0. 利用式(35),可得

(39)

若m+n≠0,将式(20)带入式(38),可得

Ln*Im=(am+n-an)Im+nm,n,m+n≠0

(40)

21) 设n≠0,由[L-n,Ln*I-n]=[L-n,Ln]*I-n+Ln*[L-n,I-n]及式(10，28，39，40),可得

于是

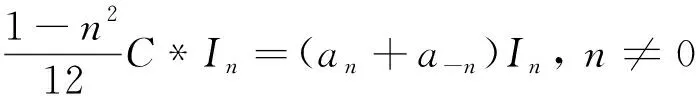
(41)

(42)

23) 由[L1,L-1*I0]=[L1,L-1]*I0+L-1*[L1,I0]及式(26～28),得0=d0I0+ν0C.于是,

d0=0ν0=0

(43)

24) 设n≠0,由[L-n,In*Ln]=[L-n,In]*Ln+In*[L-n,Ln],并利用式(20，24，28，35),可得

从而有

设n≠0,m≠0,m≠n,m+n≠0,m≠±1,利用式(16，20，24),等式

[L-n,Im*Ln]=[L-n,Im]*Ln+Im*[L-n,Ln]

左边=[L-n,(an-am+n)Im+n]=

(m+n)(am+n-an)Im

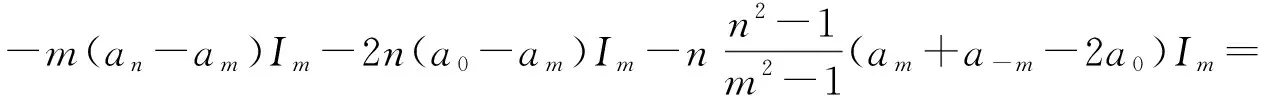
[m(am-an)+2nam-2na0]Im-

于是有

容易验证,此式分别对于n=0,m=0,m=n,m+n=0均成立,因此有

(47)

在式(47)中取n=1,结合式(37，44，45),得

(m+1)am+1=(m+2)am+a1-2a0n∈Z

(48)

对m≥1用数学归纳法,可得am=m(a1-a0)+a0. 再利用式(46),可得

an=n(a1-a0)+a0,n∈Z

(49)

显然,对任意的n∈Z都有an+a-n=2a0.式(36)变为

Ln*C=0n≠±1

(50)

25) 设L0*C=∑xiLi+∑yjIj+κC.由[L0,L0*C]=[L0,L0]*C+L0*[L0,C],即[L0,L0*C]=0可得

∑ixiLi+∑ixiIi+∑jyjIj=0

显然,当i≠0,j≠0时,xi=0,yj=0. 进一步,由[In,L0*C]=[In,L0]*C+L0*[In,C],可得

In*C=x0Inn≠0

综合式(50),可知x0=0.因此

再由[Ln,L0*C]=[Ln,L0]*C+L0*[Ln,C],可得

Ln*C=0,n≠0

(53)

根据式(52),由[L1,I-1*C]=[L1,I-1]*C+I-1*[L1,C],得I0*C=[L1,I-1*C]=0. 因此,

In*C=0 ∀n∈Z

(54)

设n≠0,由[Ln,L-n*C]=[Ln,L-n]*C+L-n*[Ln,C],即[Ln,L-n]*C=0可得

分别取n=1,n=2,易得L0*C=C*C=0.

因此,有

Ln*C=In*C=C*C=0 ∀n∈Z

(55)

26) 设n≠0,利用式(11,23，55),等式[L-n,L0*Ln]=[L-n,L0]*Ln+L0*[L-n,Ln]的

左边=[L-n,anLn+bnIn]=-n(2anL0+2anI0+

右边=-nL-n*Ln-nI-n*Ln-2nL0*L0-2nL0*I0=-n(L-n*Ln+anI0+

2a0L0+2b0I0+2μ0C)

所以

将式(49)代入,可得

(56)

27) 设n≠0,利用式(10,11，56),等式[Ln,L-n*Ln]=[Ln,L-n]*Ln+L-n*[Ln,Ln]的

左边=[Ln,(a1-a0)2nL0]=

2n2(a1-a0)(Ln+In)

右边=[Ln,L-n]*Ln=2n(anLn+bnIn)

于是有n(a1-a0)(Ln+In)=anLn+bnIn.因此

bn=an=n(a1-a0)n≠0

与式(49)相比较,知a0=0.从而

bn=an=na1∀n∈Z

(57)

进而,根据式(1，11，21，41，56)可得

类似于25),并利用式(48),可得

C*Ln=C*In=0 ∀n∈Z

28) 设n≠0,m≠0,m+n≠0,利用式(11，35，59),等式

[Lm,L0*Ln]=[Lm,L0]*Ln+L0*[Lm,Ln]

左边=[Lm,na1(Ln+In)]=

na1(m-n)(Lm+n+Im+n)-a1n2Im+n=

a1(mn-n2)Lm+n+a1(mn-2n2)Im+n

右边=mLm*Ln+mIm*Ln+(m-n)L0*

Lm+n+(m-n)L0*Im+n=

mLm*Ln-m2a1Im+n+(m-n)(m+n)×

a1(Lm+n+Im+n)+(m-n)(m+n)a1Im+n=

mLm*Ln+(m-n)(m+n)a1Lm+n+

(m2-2n2)a1Im+n

所以

因此

Lm*Ln=(n-m)a1(Lm+n+Im+n)

n≠0,m≠0,m+n≠0

(62)

29) 由[L2,L2*L-4]=[L2,L2]*L-4+L2*[L2,L-4],得

左边=[L2,-6a1(L-2+I-2)]=

因此12μ0C=0,即μ0=0.

综合1)～29)的结果,有

因此,对任意的m,n∈Z都有

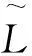
注1由定理1的证明,可以得到形变李代数L的任何Poisson代数结构都具有如下形式：

x*y=k[x,y]x,y∈L

这里k是任意常数.故而L也没有非平凡的结合Poisson代数结构.