求解三维热传导方程的高效精确算子分裂方法

武莉莉

(1. 宁夏大学 数学统计学院, 宁夏 银川 750021; 2. 宁夏师范学院 数学与计算机科学学院, 宁夏 固原 756000)

本文考虑如下三维热传导方程的初边值问题：

为了讨论方便,假设空间域Ω=[0,1]×[0,1]×[0,1].T表示温度;ν为热扩散系数;α(x,y,z)是光滑函数,g0,g1,d0,d1,l0和l1是常数.

热传导方程是一类非常重要的偏微分方程,能够描述很多自然环境和工程设备中的物理现象,比如超导体中的热传导,燃烧室内的温度分布等.只有一小部分问题能够获得精确解,绝大多数问题要得到精确解是非常困难的,甚至是不可能的,所以寻求其数值求解方法具有非常重要的理论价值和现实意义.

求解该方程的数值方法有很多,如有限差分法[1-3], 有限体积法[4], 有限元法[5-6]以及配点法和谱方法[7-8], 等等. 这些方法中有限差分方法由于格式构造简单容易理解引起了广大学者的关注. 对于高维问题而言,一个重要的方面是如何减低计算成本和如何提高计算效率. 对于高维热传导方程而言,显式差分格式由于受到苛刻的稳定性条件的限制很难应用,而全隐格式由于在每个时间层上都需要迭代求解,也存在计算量大、计算效率低下的显著缺点.为了克服这两方面的缺点,二十世纪五六十年代算子分裂方法应用而生[9-10].目前有两种算子分裂方法应用最广,其中一种是交替方向隐式(ADI )方法[8,11-16],另一种是局部一维化(LOD)方法[17-21]. 他们均可以将高维问题转化为多个一维问题来求解,而一维问题往往可以采用快速的三对角矩阵算法 (TDMA). 在目前已有的关于算子分裂方法的研究中,很多空间高精度的算法已经被提出来了, 但是时间方向的精度仍然是低精度的,这是由于传统的Peaceman-Rachford方法[11-13], Crank-Nicolson方法[8,12,16-17,20], 或者其他低阶精度的显式或者隐式方法[19,21]被用于时间的离散和处理.

本文构造时间和空间均具有高精度的数值算法,采用算子分裂的局部一维化方法将方程(1)表示为三个一维方程,再利用高精度有限差分格式和高精度Padé近似来分别离散方程(1)中的空间导数和时间导数, 从而得到两种高精度有限差分格式.从理论上严格证明格式的稳定性,给出数值实验结果.

1 算子分裂方法

根据局部一维化方法的原理,方程(1)从形式上可以分裂为三个一维方程:

为了从第n时间层获得第n+1时间层未知函数的值, 可以假设方程(6)可以实现由第n时间层获得n+1/3时间层的值, 方程(7)可以实现由第n+1/3时间层获得第n+2/3时间层的值, 方程(8)可以实现由第n+2/3时间层获得n+1时间层的值. 下一步将针对上述方程构造高精度格式.

2 高精度紧致差分格式

以τ表示时间步长,空间取等间距网格,步长用h表示。网格点为(xi,yj,zk,tn),xi=ih,yj=jh,zk=kh,tn=nτ,i,j,k=0,1,…,N,h=1/N,n≥0. 为了建立方程(6)的高精度紧致差分格式,利用如下紧致差分公式[22]:

(9)

(10)

式(10)具有空间四阶精度.添加上初始和边界条件可以得到如下的常微分方程的初值问题：

(11)

由此,很容易获得方程(11)的解为

T(t)=-B-1F+etA-1B[T(0)+B-1F]

(12)

(13)

eP=(12-6P+P2)-1(12+6P+P2)+O(P4)

(14)

(15)

式中:τ为时间步长.将方程 (15) 代入方程(13)可得

(16)

(17)

把方程 (17) 记为FOD格式.应用该格式能够实现由tn到tn+1的计算.由推导过程易知该格式时间和空间均具有四阶精度.

下面构造求解方程(1～4)的六阶精度差分格式.利用文献[1]中结论, 可以得到二阶导数的六阶精度离散格式：

(18)

(20)

为此,可以得到方程(6)在x方向的常微分方程系统:

(21)

式中

T(t),F和B的定义如前面所述.方程(21)的解析解为

T(t)=-B-1F+etD-1B[T(0)+B-1F]

(22)

离散方程 (22) 可以得

(23)

利用六阶精度的(3,3) Padé 格式[23]计算时间t的导数,可得

eP=(120-60P+12P2-P3)-1×

(120+60P+12P2+P3)+O(P6)

(24)

(25)

将式(25)代入式(23), 整理后可得

(26)

利用类似的方程处理y和z方向, 最终可以得到求解方法(6～8)的新的有限差分格式, 表示如下：

(27)

将式(27)记为SOD格式.由推导过程可知,其截断误差为O(τ6+h6).

3 稳定性分析

引理1假设λ是(N-1)×(N-1)阶矩阵A-1B的特征值,x是其相应的特征向量.则λ是实数,并且满足λ≤0.

证明假设λ是特征值,x是矩阵A-1B对应的特征向量.他们满足如下的关系:

A-1Bx=λx

或者

xTBx=λxTAx

由于

因此

xTBx<0

(28)

且有

因此

xTAx>0

上述结果即可表明λ是实数,并且满足：λ≤0.

引理2假设μ是矩阵D-1B的特征值,x是其相对应的特征向量.则μ是实数,并且满足μ≤0.

证明对于矩阵D有

利用不等式

2xy≥ -x2-y2

和

2xy≤x2+y2

可以得到

结合式(28)的结果,可以得到μ≤0.

定理1FOD格式 (17) 和SOD格式(27)均是无条件稳定的.

证明令λi(i=1,2,…,N-1)表示A-1B的特征值, 利用引理1,可以得到

由此可得

式中

令μi(i=1,2,…,N-1)为矩阵D-1B的特征值,利用引理2, 可得

因此

式中

ρ(H1)和ρ(H2)是矩阵H1和H2的谱半径.至此定理得证.

推论1FOD格式(17)和SOD格式(27)均是无条件收敛的.

证明由FOD格式(17)和SOD格式(27)的建立过程很容易得出这两种格式的截断误差分别为O(τ4+h4)和O(τ6+h6),即格式(17)和格式(27)与原微分方程(1)均是相容的.又由定理1可得格式(17)和格式(27)均是无条件稳定的,因此根据Lax等价性定理,格式 (17) 和格式(27) 均是无条件收敛的.

4 数值算例

采用两个算例来验证本文方法的性能,分别利用本文所提的FOD和SOD格式进行计算,并且为了与低精度方法进行比较,还采用了Douglas-Gunn格式[10]进行了计算.全部的计算都是在PC机上,采用Matlab语言编程完成的.

格式的收敛阶定义如下：

式中:L2-err表示L2范数误差；h1和h2分别为两个不同空间网格步长.L2-err定义如下：

算例1

0≤x,y,z≤1,t>0

该问题的分析解为

u(x,y,z,t)=e-3π2tsin(πx)sin(πy)sin(πz)

为了衡量时间精度,设定h=0.02,让时间步长τ发生变化.表1分别给出了Douglas-Gunn格式[10]、本文的FOD格式 (17)和SOD格式 (27)的计算结果.可以看出Douglas-Gunn格式时间仅有二阶精度,FOD格式具有四阶精度,SOD格式具有六阶精度.为了衡量空间精度,设定τ=0.001,让空间步长h发生变化.表2分别给出了三种格式的计算结果.结果显示本文FOD格式和SOD格式空间上也分别达到了四阶和六阶精度,而Douglas-Gunn格式精度仅有二阶.为了验证格式的整体精度,设定h=τ=1/10,1/20,1/30,1/40, 表3给出了t=0.5时刻三种方法的数值计算结果.可以看出三种格式均达到了各自理论上的精度阶.FOD格式和SOD格式整体具有四阶和六阶精度,而Douglas-Gunn格式[10]整体上仅具有二阶精度.

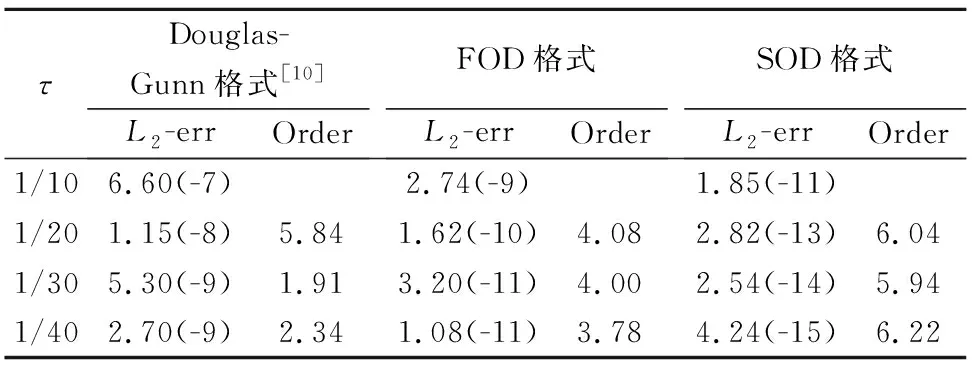
表1 算例1当h=0.02,t=0.5时,不同τ的L2范数误差及收敛阶Tab.1 L2-error and accuracy order with h=0.02,t=0.5 for Example 1

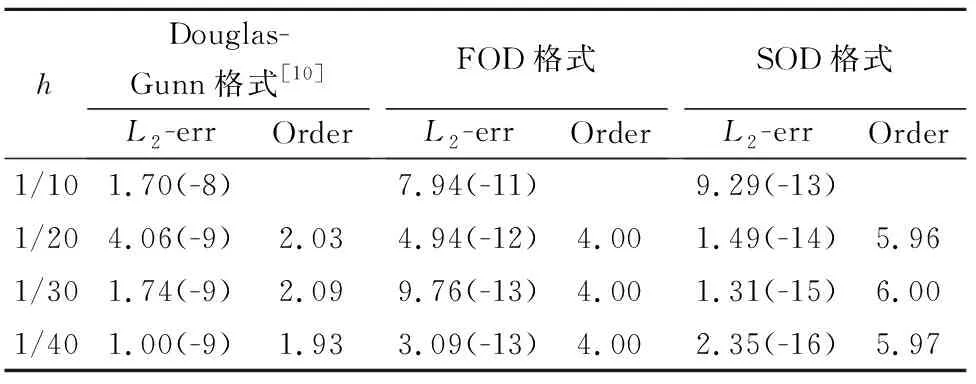
表2 算例1当τ=0.001,t=0.5时,不同h的L2范数误差及收敛阶Tab.2 L2-error and accuracy order with τ=0.001,t=0.5 for Example 1

表3 算例1当τ=h,t=0.5时的L2范数误差及收敛阶Tab.3 L2-norm error and accuracy order with τ=h,t=0.5 for Example 1

算例2:

0≤x,y,z≤1,t>0

该问题的分析解为

u(x,y,z,t)=e-4π2tsin(4πx)sin(4πy)sin(4πz)

针对算例2,为了评估本文格式的时间、空间精度以及整体精度.表4～表6给出了上述三种格式的计算结果.其中表4取定空间步长h=0.012 5,让时间步长τ变化,考察了时间精度；表5取定时间步长τ=0.005,让空间步长h变化,考察了空间精度；表6让时间步长和空间步长同时变化,考察了格式的整体精度.通过三种格式的数值结果比较,仍然可以得到与理论分析相一致的结论.

表4 算例2当h=0.012 5,t=0.5时,不同τ的L2范数误差及收敛阶Tab.4 L2-error and accuracy order with h=0.012 5 at t=0.5 for Example 2

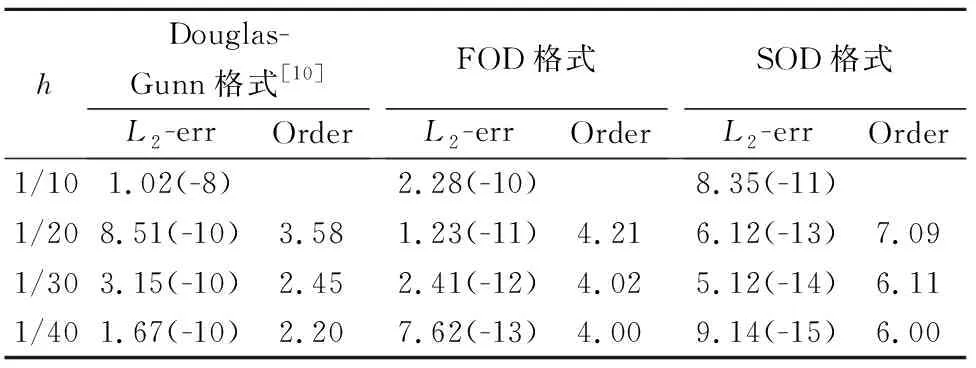
表5 算例2当τ=0.005, t=0.5时,不同h的L2范数误差及收敛阶Tab.5 L2-error and accuracy order with τ=0.005 at t=0.5 for Example 2

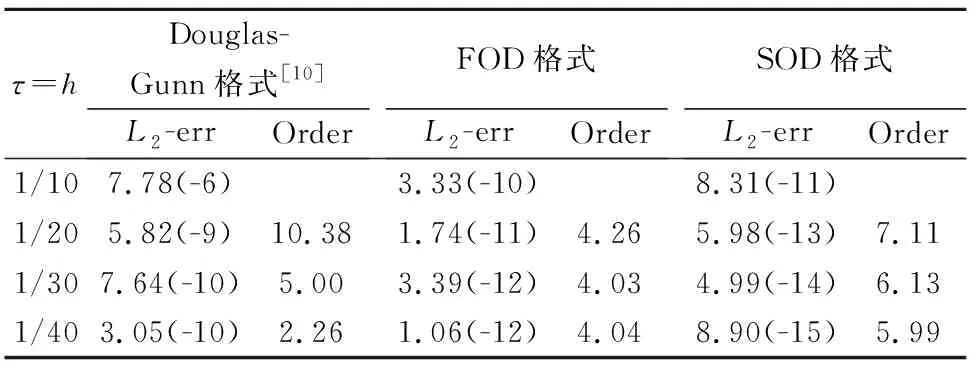
表6 算例2当τ=h, t=0.5时的L2范数误差及收敛阶Tab.6 L2-norm error and accuracy order with τ=h at t=0.5 for Example 2

5 结论

本文提出了数值求解三维热传导方程的两种局部一维化算子分裂方法,该方法把三维问题转化为三个一维问题来求解.空间方向分别采用四阶和六阶紧致差分离散,而时间方向分别采用(2,2) Padé式和(3,3) Padé公式进行离散,最终获得了整体具有四阶精度和六阶精度的两种差分格式,其截断误差分别为O(τ4+h4)和O(τ6+h6).通过矩阵理论分析严格证明了两种格式均是无条件稳定的.通过数值实验验证了两种格式均可达到各自的理论精度.本文方法较已有文献中方法[8,11-13,16-17,19-21]的优势在于时间方向也达到了高精度,并且由于采用了局部一维化方法,因此同时保证了算法的高效性.

致谢：本文得到宁夏师范学院校级科研项目(NXSFZDA2001)的资助,在此表示感谢.