求平面向量模的最值问题思路举隅

安徽 祝 峰

平面向量具有“数”和“形”的双重性，是沟通几何、代数和三角的工具.平面向量的模是一个实数，是平面向量的核心概念，具有明确的几何意义，与平面向量的运算紧密相关.这使得平面向量的模在试题中常出现在知识点的交汇处，特别是模的最值问题，着眼于向量知识，与函数、方程、三角、不等式和解析几何联系，思维跨度大且解法灵活.下文拟通过实例列举求解平面向量模的最值问题的三种思路，供参考.

一、坐标运算(解析法)

在平面向量模的最值问题的求解中，通过建立平面直角坐标系，就能把向量的条件“坐标化”“方程化”和“解析化”，明确向量模的几何意义.这样可避免繁杂的逻辑推理过程，通过解析运算即可解决问题.

【例1】平面向量a，b，c满足|a|=1，|b|=2，a·b=1，(a-c)·(b-c)=0，则|2a+c|的最大值为

( )

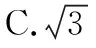
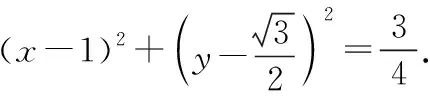
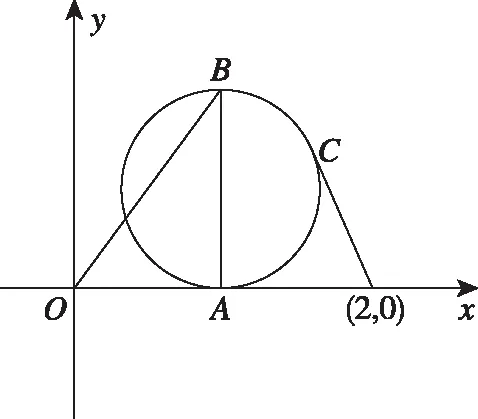
【评析】如果纯粹从向量运算的角度考虑问题会很难着手，原因有二：①条件(a-c)·(b-c)=0在说明什么？也就是说c具有什么性质很难被发现，这恰好又是解决这个问题的关键；②|2a+c|的几何意义是什么？隐藏很深，不易被察觉.两个问题在建立平面直角坐标系进行坐标运算后即可迎刃而解，我们称这样的思路为“解析法”.

二、平面几何(几何法)

平面向量及其线性运算和数量积运算均有明确的几何背景，在平面向量模的最值问题求解中可从向量模的几何意义出发，结合图形的几何特征，利用平面几何知识，直观地解决模的最值问题.

( )

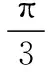
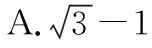
【评析】此例也可以像例1一样用解析法解答，但这个问题中|a-b|变化的本质因素b所满足的条件|b-2e|=1的几何意义明显，容易构造几何图形，利用图形性质结合平面几何有关知识可解决.我们称这样的思路为“几何法”，即赋予向量条件几何意义，用平面几何知识求解模的最值.

三、不等式(不等式法)

(一)三角形不等式

利用向量加减法的三角形法则及三角形两边之和大于第三边可得如下不等式：

|a|-|b|≤|a±b|≤|a|+|b|(当a=λb时取等号)，我们称其为“三角形不等式”( 当a，b是复数时这个不等式也成立).在向量模的最值问题的求解中，可以用它来解决.

( )

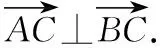
A.6 B.7

C.8 D.9

【评析】在求向量和差的模的最值时，可以考虑三角形不等式，需注意的是等号取到的条件，只有等号取到时，才能取到最值.对于|a±b|≥|a|-|b|，可以加强为|a±b|≥||a|-|b||用于求最小值，当且仅当a，b共线且反向时取等号.

(二)均值不等式

任意实数a，b∈R*，有如下不等式成立：

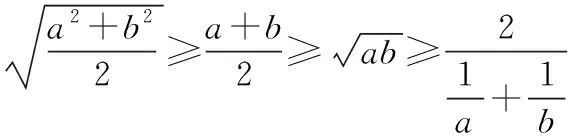
【例4】已知向量a，b满足|a+b|=|a-b|=5，则|a|+|b|的取值范围是

( )

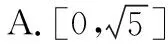
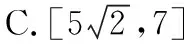
(三)柯西不等式

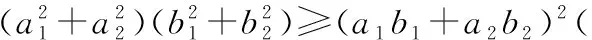
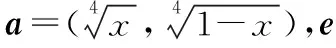
【评析】柯西不等式应用广泛.尤其是在不等式证明和向量积的最值问题求解中，灵活巧妙地应用它，可以使一些较为困难的问题迎刃而解.|a·e|严格来说并不是向量的模，但其是与|a|，|e|有联系的一个量，也视其为向量模的最值求解问题.

四、函数(函数法)

向量的模的变化如果是由变量导致，可以建立向量模与变量之间的函数关系，问题即转化为求函数最值的问题.

( )

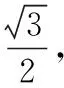
【解析】设e1，e2夹角为θ，则

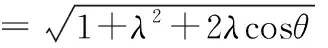
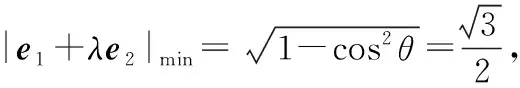
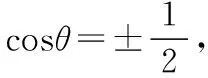
【评析】把|e1+λe2|视为λ的函数，求取得最小值时的θ值，进而可求|e1+e2|，向量模有最值的根本原因是其在变化，函数是描述变化直接的手段，求解向量模的最值问题过程中，函数思想应占有重要位置.