非线性分数阶常微分方程组的Euler方法
代 跃,周晓军
(贵州师范大学 数学科学学院,贵州 贵阳 550025)
0 引言
分数阶微积分和经典微积分研究几乎同时开始[1],但由于分数阶微积分的实际应用受限,及缺乏物理背景的支持,发展缓慢。但分数阶微积分具有描述物质记忆功能和遗传效应的特征,使得它比整数阶导数的描述更加精确。近年来,分数阶微积分被广泛的应用在自然科学和工程计算[2-3]的诸多领域内。如被用来描述粘弹性材料、材料的电性质、电磁波、电化学过程,动力系统中的控制理论,生物系统中的电导、混沌、神经细胞中离子的反常扩散、生化、水文、金融及其他应用领域中的问题。分数阶微积分理论也受到越来越多的国内外学者的广泛关注,特别是从实际问题抽象出来的分数阶微分方程成为很多数学工作者的研究热点。
由于分数阶微分的解析解很难求得,所以像整数阶一样借助数值方法求解是一个好的选择。因此,研究分数阶微分方程的数值算法成为一个热点。至今,已提出了许多经典的数值方法[4-7]:Diethelm等[4]提出一种Adams型的预估-校正方法,并给出了这种算法的误差分析;Lin等[5]在Lubich方法的基础上,提出了一种线性多步法来求解分数阶微分方程初值问题,并证明了该方法的相容性、收敛性和稳定性;Kumar等[6]利用求解Volterra方程的block-by-block方法设计了一类新的分数阶block-by-block方法,数值算例也证明了此方法的有效性和稳定性,但并没有作出证明;李[7]推导出了分数阶积分的Chebyshev小波矩阵,并利用它来求解了非线性分数阶微分方程。
本文考虑非线性分数阶微分方程组初值问题
(1)
已有一些文章对该方程组进行研究,Varsha Daftardar-Gejji等[8]对方程组解的存在性、唯一性以及稳定性进行了论证。林永华等[9]根据分数阶导数的高阶近似提出了分数阶微分方程组的高阶近似法。童启秀等[10]利用求解普通积分方程的Adams技巧,建立了分数阶微分方程组的一种显式数值算法。代群等[11]使用变分迭代法求解分数阶微分方程组,并改进了校正函数。栾新等[12]根据延迟校正法的思想来设计求解分数阶微分方程组初值问题的高精度格式。
田献珍等[13]将求解整数解方程的Euler法应用于非线性分数阶常微分方程模型。本文对Euler法进行推广,将方程组(1)转化为积分方程组后对每一个积分方程应用Euler法,得到了方程组(1)的隐式算法,并证明了算法的收敛性及稳定性,最后给出了数值实例。
1 预备知识
引理1[14]若连续函数y(t)是初值问题
(2)
的解,则y(t)是第二类Volterra积分方程:
的解,反之亦然。

由引理1可将方程组(1)转化为如下的Volterra积分方程组:
(3)
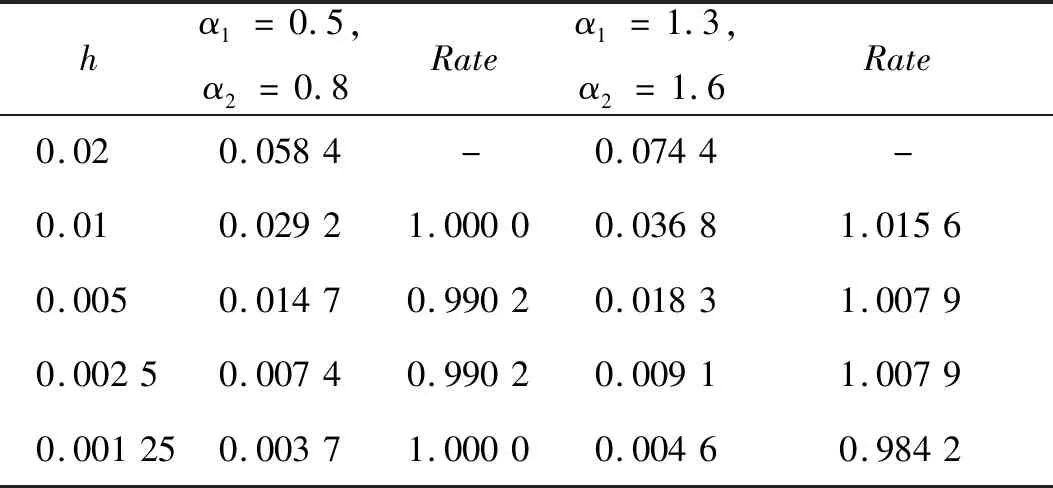
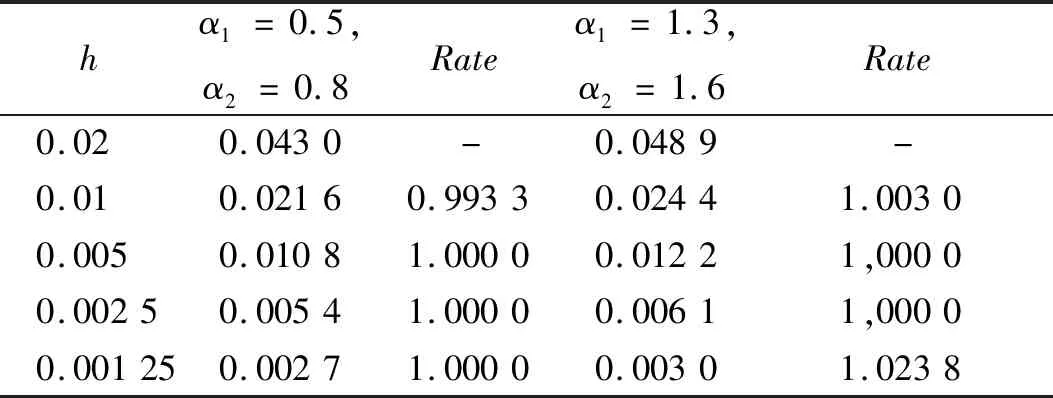
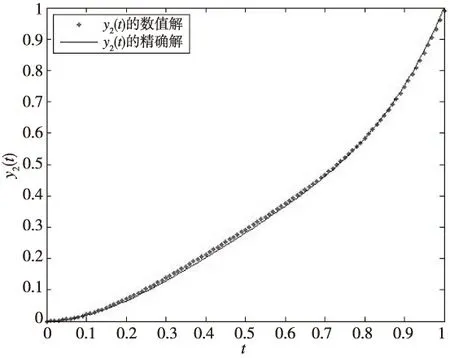
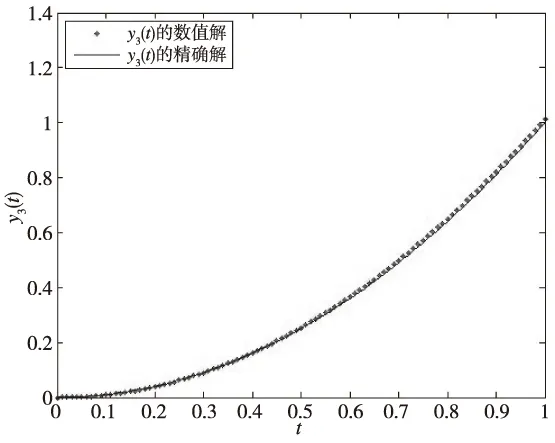
引理2[15]设β,γ≥0,h>0,Nh≤(b-a),0 则必有 ηm≤βEα(γΓ(α)(mh))α,m=0,1,2,…,N 其中 是单参数Mittag-Leffler函数。 对方程组(3)的每一个积分方程采用文献[13]中所用的积分方法。首先进行网格剖分:取均匀网格节点tj=jh,j=0,1,2,…,N,h=T/N是积分步长。(2)式中取t=tm得: 类似于数值积分的处理方法:在子区间[tj,tj+1],j=0,1,2,…,m上,若用fi(tj+1,y1(tj+1),y2(tj+1),…,yz(tj+1))近似代替fi(t,y1(t),y2(t),…,yz(t)),得: 令 yi,j≈yi(tj),gi,j=gi(tj),fi,j=fi(tj,y1(tj),y2(tj),…,yz(tj))。 得 (4) (5) 我们称式(4)和(5)为分数阶隐式Euler法。 引理3[13]当z=1时,分数阶微分方程组(1)退化为分数阶微分方程(2)。设α>0,y(t)充分光滑,且CDαy(t)∈C1[0,T],函数f(t,y)关于第二个变量满足Lipschitz条件,则分数阶隐式Euler法的误差满足: 定理1 设fi(t,y1(t),y2(t),…,yz(t))∈C3(0,T),i=1,2,…,z,z≥2。则有分数阶常微分方程组隐式Euler法(4)的误差满足: 为证明这个定理,需要用到引理3。 证明 令Y(t)=(y1(t),y2(t),…,yz(t)),则:fi(t,y1(t),y2(t),…,yz(t))=fi(t,Y(t))。 当t=t0时,|yi(t0)-yi,0|=0,等式成立。 当t=t1时, |yi(t1)-yi,1|= 由引理3得 |yi(t1)-yi,1| 其中 令 得 当t=tm时, |yi(tm)-yi,m|= 由引理3: 又有: 证明 由 两式相减,得: 因为 所以有 则由Gronwall不等式可得存在常数C,满足: 例1 考虑非线性分数阶微分方程组 初始条件为: y1(0)=y2(0)=0,0≤t≤1, y1′(0)=y2′(0)=0,(αi>1)。 该非线性分数阶微分方程组的一组精确解为: 表1 α1=0.5,α2=0.8和α1=1.3,α2=1.6,y1的最大误差随时间步长h的变化与收敛阶Tab.1 α1=0.5,α2=0.8 and α1=1.3,α2=1.6 change of the maximum error of y1 with time step h and order of convergence 表2 α1=0.5,α2=0.8和α1=1.3,α2=1.6,y2的最大误差随时间步长h的变化与收敛阶Tab.2 α1=0.5,α2=0.8 and α1=1.3,α2=1.6 Change of the maximum error of y2 with time step h and order of convergence 图1 α1=0.5,α2=0.8和α1=1.3,α2=1.6在h=0.01时y1(t)的数值解和精确解曲线Fig.1 Analytical solution and numerical solution for y1(t)with α1=0.5,α2=0.8 and α1=1.3,α2=1.6 when h=0.01 图2 α1=0.5,α2=0.8和α1=1.3,α2=1.6在h=0.01时y2(t)的数值解和精确解曲线Fig.2 Analytical solution and numerical solution for y2(t)with α1=0.5,α2=0.8 and α1=1.3,α2=1.6 when h=0.01 例2 考虑非线性分数阶微分方程组 初始条件为:y1(0)=y2(0)=y3(0)=0,0≤t≤1, y1′(0)=y2′(0)=y3′(0)=0,(αi>1)。 该非线性分数阶微分方程组的一组精确解为: 表3 α1=0.5,α2=0.6,α3=0.7和α1=1.1,α2=1.2,α3=1.3,y1的最大误差随时间步长h的变化与收敛阶Tab.3 α1=0.5,α2=0.6,α3=0.7 and α1=1.1,α2=1.2,α3=1.3Change of the maximum error of y1 with time step h and order of convergence 表4 α1=0.5,α2=0.6,α3=0.7和α1=1.1,α2=1.2,α3=1.3,y2的最大误差随时间步长h的变化与收敛阶Tab.4 α1=0.5,α2=0.6,α3=0.7 and α1=1.1,α2=1.2,α3=1.3Change of the maximum error of y2 with time step h and order of convergence 表5 α1=0.5,α2=0.6,α3=0.7和α1=1.1,α2=1.2,α3=1.3,y3的最大误差随时间步长h的变化与收敛阶Tab.5 α1=0.5,α2=0.6,α3=0.7 and α1=1.1,α2=1.2,α3=1.3Change of the maximum error of y3 with time step h and order of convergence 图3 α1=0.5,α2=0.6,α3=0.7在h=0.01时y1(t)的数值解和精确解曲线Fig.3 Analytical solution and numerical solution for y1(t) with α1=0.5,α2=0.6,α3=0.7 whenh=0.01 图4 α1=0.5,α2=0.6,α3=0.7在h=0.01时y2(t)的数值解和精确解曲线Fig.4 Analytical solution and numerical solution for y2(t)with α1=0.5,α2=0.6,α3=0.7 whenh=0.01 图5 α1=0.5,α2=0.6,α3=0.7在h=0.01时y3(t)的数值解和精确解曲线Fig.5 Analytical solution and numerical solution for y3(t)with α1=0.5,α2=0.6,α3=0.7 whenh=0.01 本文提出用分数阶Euler法来解一类非线性分数阶常微分方程组,并证明了该数值方法的收敛性和稳定性,所举的数值例子也证实了分数阶Euler法是解这类非线性分数阶常微分方程组的一个有效方法。2 Euler法
3 收敛性分析

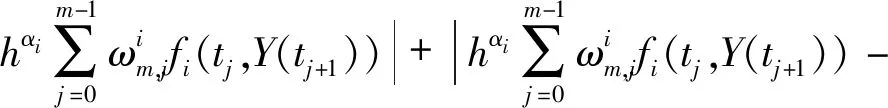

4 算法稳定性分析



5 数值实验








6 结论

