基于分区域双边滤波的谷粒噪声修复算法

徐 敏， 丁友东， 董 荪， 张倩倩， 李傅媛， 陈 钰

(1. 上海大学上海电影学院， 上海200072;2. 上海大学上海电影特效工程技术研究中心， 上海200072)

目前， 中国电影资料馆的胶片库存有3 万多部、60 多万本， 但由于年代久远、保存不当以及转印、播放次数过多等因素造成影片有许多损伤， 因此加紧胶片电影数字化修复工作已是迫在眉睫. 噪声是数字化修复中比较常见的全局性损伤， 常见的噪声有闪烁噪声、划痕噪声、霉斑噪声、谷粒噪声和白噪声5 种类型， 其中最具代表性的是谷粒噪声. 去噪是图像预处理中很关键的一步， 旨在减小视频图像中的噪声的同时， 尽可能地保留边缘和纹理信息. 目前较常用的有空域和变换域两种去噪方式， 而适用于谷粒噪声消除的算法大致有4 种， 即非线性阈值去噪法、基于统计学的去噪算法、基于线性最小均方误差的去噪算法和自适应去噪法. 文献[1]能有效消除谷粒噪声， 但同时也删掉了图像的部分细节. 文献[2]适用于斑点噪声去除和图像边缘检测. 文献[3]在保护结构的基础上去除噪声， 却没有利用图像的整体结构及区域信息. 文献[4]能较好保留图像的细节和纹理且应用广泛. 此外， 很多学者利用彩色图像本身三通道之间的有机联系进行去噪[5-7]， 但算法的复杂度很高. 市场上也有很多专门去除谷粒噪声的图像修复软件和降噪工具， 但却是或价格昂贵， 或效果不好. 本工作提出基于分区域双边滤波的噪声修复算法， 目标是去除胶片电影中常见的谷粒噪声， 为后续斑点、划痕、稳像、闪烁等修复工作提供质量保证.

1 算 法

本工作的去噪原理是通过研究含噪图像， 寻找图像特征或信息分布规律， 对像素值直接进行滤波处理， 从而达到去除噪声的目的， 因此寻找胶片上谷粒噪声的产生原因及其在图片上的分布特征是消除谷粒噪声算法中很关键的一步.

1.1 谷粒噪声特性

谷粒噪声是光线照射到卤化银上发生化学作用而产生的， 具有很多不可控因素， 如胶片过期， 储藏室环境的温度、湿度、光照控制不稳定， 过曝或欠曝， 胶片感光度过高等. 谷粒噪声的特征呈大小不一、随机排列的颗粒状， 直方图接近高斯分布， 在帧与帧之间独立存在且在时间轴方向没有相关性， 噪点位置与周边像素点的灰度值不同， 以纯黑、纯白色噪点数量居多. 根据黑白负片的形成原理， 将胶片底片中银的密度d 和曝光量e 之间的对数关系表示为[8]

根据式(1)， 可变形得到式(2)， 即从密度域到曝光域的反变换，

假设胶片图像为re(m，n)， 且se(m，n)， vd(m，n)分别表示胶片在曝光域、密度域受噪声影响的图像， 则re(m，n) = ve(m，n)se(m，n). 根据式(2)可将从密度域接收图像变换到曝光域接收图像表示为

根据式(3)可知， 底片上的零均值方差固定的高斯噪声vd(m，n)， 在经过显影处理后， 获得了具有典型谷粒噪声特性的曝光域图像噪声ve(m，n)， 因此认为胶片电影中的谷粒噪声是依赖于信号的乘性非高斯噪声模型.

1.2 噪声模型表示

图 1(a) 是 m × n 大小的视频序列中第 t 帧含有谷粒噪声的图像， 记为 I(x，y，t)，x ∈(0，m-1)，y ∈ (0，n-1); 图 1(b)是原图像红色方框处的局部放大效果， 可见有很多不同大小且呈颗粒状的噪点.

图1 谷粒噪声样图Fig.1 Grain noise pattern

在图像去噪前， 需建立谷粒噪声模型， 其中乘性高斯噪声模型和加性高斯噪声模型应用最为广泛. 假设n(x，y，t)为第t 帧图像上待去除的噪声， c(x，y，t)为第t 帧图像去噪后的干净原始图像， 则待修复图像的加性噪声模型、乘性噪声模型如下:

由式(4)可以看出， 加性噪声叠加在视频原始信号之上， 与原始信号不相关; 而式(5)则说明乘性噪声是原始信号灰度的放大与缩小， 与原始信号密切相关. 接下来将作更详细的算法描述与实现， 并通过几组对比实验， 突出本算法在谷粒噪声修复中的良好性能.

2 算法描述与实现

在图像的不同区域， 受到图像信号的影响， 谷粒噪声的大小也会发生变化， 这使得研究去除谷粒噪声的模型也相对困难. 面对实际电影胶片中存在的结构多样化、损伤程度不一致的谷粒噪声， 本工作提出的算法实现的前提是利用图像本身RGB 三通道的相关性依次对谷粒噪声进行运动检测、噪声识别、图像去噪和图像增强.

2.1 运动检测

由于后一帧与当前帧存在延时， 故选择当前帧(第t 帧)的前两帧(第t-1 和t-2 帧)来辅助计算运动矢量 d(dx，dy，t)， 再根据 d(dx，dy，t)是否大于 D1来判断当前帧的像素运动. 通过绝对差法计算得到第t 帧与第t-1 帧的运动矢量d1，

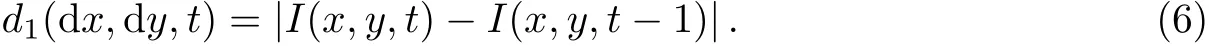
如果d1(dx，dy，t)＞ D1，则认为第 t 帧与第 t-1 帧在(x，y)位置存在像素运动，即 d(dx，dy，t)=0; 否则， 继续计算第t 帧与第t-2 帧的运动矢量d2，

如果 d2(dx，dy，t)＞ D1，则认为第 t 帧与第 t-2 帧在(x，y)位置存在像素运动，即d(dx，dy，t)=1; 否则， 认为第 t 帧与第 t-1， t-2 帧在(x，y)位置都不存在像素运动， 即d(dx，dy，t)=2.

2.2 噪声识别

在正常情况下， 同一图像序列中相邻帧上同一个像素点的运动矢量值是相等的. 假设第t 帧图像上的像素点 E(x，y)的运动矢量就是(dx，dy，t)， 则 E 点在 t-1，t+1 帧的匹配位置分别为(x-dx，y-dy，t-1)， (x+dx，y+dy，t+1). 设 E 的亮度空间梯度为

利用人眼对亮度变化敏感程度不同的特性， 将G1， G2， G3三者中值较小的2 个像素的亮度平均值作为背景色 G(x，y，t). 假设三者中的最大值与 max 相等， 则 G(x，y，t) =(G1+G2+G3-max)/2. 令ΔE1， ΔE2， ΔE3分别为第 t-1， t， t+1 帧与背景色的差值， 结合韦伯定律定义噪声判定公式，

如果 ΔE2＜ T(x，y，t)， 则 E 点为“干净”的像素点; 如果 ΔE2＞ T(x，y，t) 且 ΔE1＜T(x，y，t)， ΔE3＜ T(x，y，t)， 则 E 点为极大概率受噪声污染的像素点， 但如果得到 E 点邻域内还存在这样的点， 则确定E 点为噪点， 反之则被视为“干净”的像素点; 如果上述两个条件都不满足， 则E 点为可疑像素点.

2.3 图像去噪

本工作将从空间域上分别对图像的细节区域、平坦区域进行滤波去噪处理. 细节区域即边缘或纹理细节丰富的区域， 平坦区域即像素值变化小且纹理细节较少的区域. Sobel算子认为邻域内距离不同的点， 对算子结果产生的影响不同[9]. 距离越远， 权值越小， 产生的影响越小. 定义水平算子S1和垂直算子S2如下:

则原图x 方向上的卷积V(x，y，t)和y 方向上的卷积H(x，y，t)分别为

如果 H(x，y，t)或V(x，y，t)中任一项大于阈值 T， 则认为该像素属于细节区域， 反之则属于平坦区域.

2.3.1 细节区域去噪

由于细节区域包含边缘， 而边缘点在图像滤波过程中很容易被识别为噪点， 因此对细节区域去噪前会根据邻域像素点的相关性对窗口内的噪点进行二次判别. 假设当前邻域窗口大小为 (2n+1)× (2n+1)， Imid， Ix∈Wn，y∈Wn(x，y，t)， mean(I(x，y，t))分别表示滤波窗口 Wn的中点、窗口内像素点的灰度值和灰度值对应的均值. 噪声检测因子μ(x，y，t)可表示为

当 μ(x，y，t) ≥ R 时， 判定窗口含有噪声点， 则输出邻域内像素点归一化后的加权值;当μ(x，y，t) ＜R时， 判定该像素点是边缘点， 按原值输出窗口内的像素点. 本工作取3×3的邻域窗口， min(μ(x，y，t))， max(μ(x，y，t))分别表示 μ(x，y，t)的最小值和最大值， 阈值 R 为

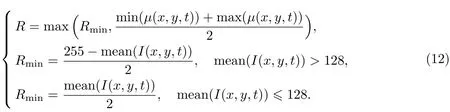
接着， 对细节区域的噪点作自适应加权平均滤波去噪处理[10]. 定义加权系数为

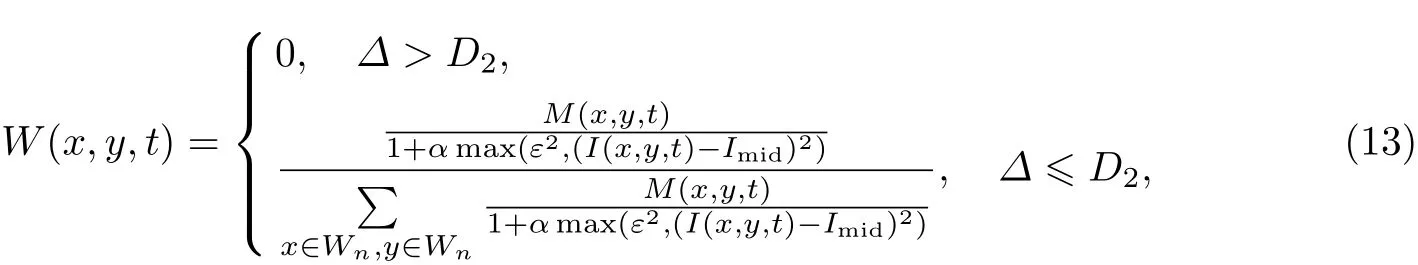
式中: Δ为窗口内其他像素与当前像素的绝对差; D2为判断阈值; M(x，y，t)是归一化常数;α和ε都是滤波器的参数. 噪点修复公式为

2.3.2 非细节区域去噪

对于非细节区域， 采用中值滤波， 运用滤波窗口邻域内的中值像素点代替中心像素点[11]，

2.3.3 彩色图像去噪

对于彩色图像， 运用三通道之间的相关性计算权重， 再分别进行滤波. 对于细节区域， 同理采用自适应加权滤波去噪算法. 首先， 定义彩色图像的权重，

式中: Ix， Iy分别是以x， y 为中心的图像块内的像素点; λβ2是归一化参数; max 的作用是当距离D 小于0 时， 权重为1. 再根据权重分别对R， G， B 通道进行滤波，

对于非细节区域， 同理采用中值滤波分别对R， G， B 通道进行滤波，

2.4 图像增强

本工作采用减小噪声幅值的方式消除噪声， 去噪后的图像边缘会变模糊， 下一步需要通过提高图像的高频分量进行图像增强. 通过对原图的直方图均衡化来增强图像， 即通过分析源图像直方图均衡化后各像素的灰度值， 计算出原始直方图分布， 进而求出原图像灰度级到目标图像灰度级的灰度映射关系. 重复操作直至得出所有的映射关系， 最后按照映射关系对原图像各像素点进行灰度转换， 实现图像增强.

3 实验测试和结果分析

采用 Matlab 实现测试， 运行环境为 Intel 1.8 GHz 处理器， 4 GB 内存. 如图 2 所示， 测试素材从左至右依次是286×286 人工添加的谷粒噪声图， 756×466， 1 268×960 胶片电影中截选的真实素材.

图2 谷粒噪声测试素材Fig.2 Test material for grain noise

采用均值滤波算法对图像进行滤波(见图3)， 可见画面明显变平滑， 但进一步观察细节发现， 五官没有立体感， 嘴巴和鼻子也随之不见. 图4 展示的是4 种去噪算法的修复效果， 包括线性最小均方误差估计(linear minimum mean square error， LMMSE)算法、格子Bolzmann方法(lattice Bolzmann method， LBM)、基于人眼感知噪声分割的综合去噪(human visual percept noise variance segmentation based synthesized grain noise removal， HSS) 算法和本算法.

图3 均值滤波去噪效果Fig.3 Denoising effect of mean filtering

图4 4 种算法的修复效果对比Fig.4 Comparison of repair effects of four algorithms

本工作从主观评价和客观评价两个方面来判定算法优劣.

(1) 主观评价. 通过观察图4 中3 组实验的修复效果发现， 针对人工添加的谷粒噪声， 利用LMMSE 算法和LBM 修复后效果都太过平滑， 而针对真实的谷粒噪声， 这两种算法几乎不起作用; HSS 算法[12]对两种条件下谷粒噪声的修复效果都比较明显， 且整体上起到了保护细节信息和避免过度平滑的作用. 但与HSS 算法相比， 本算法去噪后的图像在主观效果上更好， 画面颗粒感明显下降且边缘处理得相对较好. 进一步观察图4 中框选出来的信息比较集中的细节处发现， 本算法修复的图像更清晰自然， 且画面效果更“干净”.

(2) 客观评价. 客观评价方法是通过去噪后的图像偏离原始图像的误差程度来计算的，常用的方法有PSNR， SSIM 和算法运行时间. 通过表1 可知， 运用本算法去噪后的图像的PSNR值明显提高， 均在25 dB 以上， 同时SSIM 值均在0.75 以上， 性能明显优于其他算法，且计算时间几乎缩短为原来的一半.

表1 4 种算法的客观评价标准对比Table 1 Comparison of objective evaluation criteria of four algorithms

4 结束语

传统的图像滤波算法都过度重视PSNR 值， 且不考虑人眼的视觉特性， 导致修复后的图像过于平滑且损失了很多高频信息， 最终的视觉观感不佳. 本工作提出的算法有效融合了多种算法的优势， 合理避免了一些算法缺陷， 创新之处在于着眼人眼对噪声的容错特性以及大多数颗粒噪声自身特征， 提出针对含有噪点的细节区域和平坦区域分别进行不同的滤波处理. 实验结果证明本算法不论对人工添加的谷粒噪声， 还是真实胶片中的谷粒噪声， 都有较好的去噪表现. 但对于背景复杂的图像以及其他种类的噪声， 修复效果仍不理想.