单源点疏散问题的Online探索算法研究

胡秀婷，谢玉莹，包敏泽，蒋 波，杨玉晗

1(大连海事大学 信息科学技术学院，辽宁 大连 116026) 2(华为技术有限公司 华为北京研究所，北京 100000)

1 问题描述

本文研究的问题是关于单源点疏散问题的online快速撤离算法.所谓单源点疏散问题，简称“单源点问题”，是指受灾人员位于危险区域中的同一位置，需要快速地撤离出该区域并到达安全区域.由于危险区域的边界(安全区域)对受灾人员而言往往是未知的，所以受灾人员需要采取某种策略探索出安全边界.一般而言，称边界信息未知的一类搜索问题为online探索问题，而边界信息已知的搜索问题则称为offline搜索问题.由于缺乏边界信息的引导，使得online探索问题相对于一般搜索问题而言要复杂很多.近年来，人们提出了很多疏散问题的撤离策略，本文的研究目标是设计出一个更为高效的探索危险区域安全边界的撤离算法.

为了衡量撤离算法的效率，人们提出了竞争比的概念.所谓竞争比，是指online探索策略所花费的代价与该问题在边界信息已知情形下所设计出的最优搜索策略(offline搜索策略)的代价之比.显然，所谓“快速”或“好”的online探索策略是指竞争比较小的求解方法.探索策略的代价可用耗费的时间或路径长度来衡量，因为求解这类问题时的移动速度一般都假设是匀速的.

本文研究单源点疏散问题，将受灾人员分为1组或多组，分别提出了三角形疏散策略和半圆疏散策略，以降低撤离算法的竞争比，提升撤离算法的效率，同时解决了受灾区域为非凸多边形的单源点疏散问题.

2 单源点疏散问题的探索策略

针对单源点疏散问题的研究，约定如下：

1)对1组疏散问题，将受灾区域的边界设定为凸多边形；

2)受灾人员的撤离速度是相同的；

3)受灾区域的边界与受灾人员的初始位置是未知的，但在疏散过程中，受灾人员之间可以相互通信，共享位置信息；

4)在疏散过程中，当其中一组受灾人员探索到未知区域边界时，其余组人员可以获得该信息并立即(没有时间延误)改变疏散方向，朝着已发现的边界移动.

假设将危险区域记为P，它是一个简单多边形.受灾人员在P中的初始位置记为O，点m与点n间的线段长度记为|mn|，Dopt表示最优的offline路径长度，S(m，n)表示m点与n点之间的路径.竞争比记为k，可通过公式(1)计算：

(1)

其中，Sonline表示online探索的路径长度；Soffline表示offline搜索的路径长度.

2.1 单源点单组三角形疏散策略

假设受灾人员首先沿横坐标向右移动单位长度d，然后按逆时针方向旋转45°，继续移动长度d，接着再按逆时针方向旋转108°18′，并移动d，这时受灾人员又到达了横坐标上，完成了一次三角曲线移动(从横坐标轴到横坐标轴，并做了两次旋转).接着，按逆时针方向旋转71°42′(与横坐标轴的夹角为45°)，并移动2d，再按逆时针方向旋转108°18′，并移动2d，又一次回到横坐标轴并完成了第2次三角曲线移动.重复这个过程，直到发现P的边界.

一个三角曲线移动的示例如图1所示.由于∠ODA=45°，若|OC|=|OD|，则∠CAD为直角.在OC延长线上确定点B，使得|OC|=|BC|，则有|OB|=2*|OD|，且∠CAB=18°18′，所以在点A处旋转108°18′的目的是构造|OB|=2*|OD|的移动策略，以便计算移动路径的长度.由于移动过程中按照逆时针方向旋转了两次，所以移动路线与水平方向上呈三角形形状，故称其为三角形疏散策略.

图1 三角曲线移动的示例Fig.1 Instance of moving in trigonometric curve

由于第i项是第i-1项长度的2倍(i≥2)，所以三角形策略实际上是“双倍策略”[6]在平面上的拓展应用，受灾人员移动的路线在平面上可以看成是一个个三角形.受灾人员的疏散过程如图2所示.

图2 三角形疏散策略的移动过程Fig.2 Moving process of triangle evacuation strategies

为计算疏散策略的竞争比，需要分析相应策略在最坏情形下的移动路径程度，以及在边界信息已知情形下的最短移动路径，即Soffline.如图2所示，online情形的最坏情形是：上一次三角曲线移动已经很接近P的边界，但没有碰到边界，如图2中的粗虚线所示.进入当前三角曲线移动后，在点F处也很接近P的边界，连接EF，从O点向P边界做垂线，分别交线段EF和P边界于M和D点，|OD|是O到P边界的最短距离，即Soffline.由于受灾人员在M点没有碰到P边界，所以有 |OM|<|OD|.又因为受灾人员做第n次三角曲线移动时已经非常接近但没有碰到P边界，考虑到P是凸多边形，因此最坏情形是受灾人员在第n+1次三角曲线移动时仍然碰不到P边界，但在第n+2次三角曲线移动过程中必然穿过P的边界，如图2中点T所示.因此，受灾人员的移动路径长度Sonline可按如下方法计算：

受灾人员所走的路径为：

(2)

其中，|N′T|表示最后一次做三角曲线移动时(没有完成)所移动的距离，它等于第n+1次三角曲线移动的短边长度，有：

(3)

Soffline=|OD|是边界信息已知情形下的最短路径，且有|OM|<|OD|，所以可计算出|OM|并用它代替Soffline计算竞争比.如图2所示，在ΔOEF中，由于|OF|=2|OE|，所以可计算出∠OFE的角度，进而利用相似三角形的特性，可计算出|OM|长度.考虑一般情形，有：

(4)

因此有竞争比为：

上述结果表明，单源点单组三角形疏散策略的竞争比不超过19.48，它优于文献[6]给出的竞争比为19.64的半圆疏散策略，但又比“双倍策略”的竞争比理论下界9高出1倍多.当然，和所有单组疏散策略一样，单组三角形疏散策略也不能很好地处理危险区域P是非凸多边形的情形.

2.2 单源点2组半圆疏散策略

对于分组数为2的单源点疏散问题，由于两组人员始终沿着相反的方向进行疏散，所以最终肯定会有一组人员探索到距离其最近的边界，因此，分组数为2的单源点半圆疏散策略可以解决受灾区域为非凸多边形的疏散问题.图3给出了简单非凸多边形的部分边界.

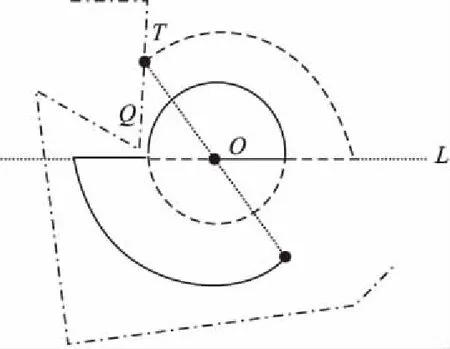
图3 半圆疏散策略的移动过程Fig.3 Moving process of semicircle evacuation strategies

当疏散人员被分为n(n≥2)组时，半圆搜索策略的多组人员通过由内向外疏散，其疏散路径构成了一个圆，所以无论凹顶点出现在平面内的任意位置，总会有一组疏散人员可以发现疏散区域中凹顶点所在的边界，图3给出了分组数为2时的一种疏散情形.当其中一组疏散人员无限接近于Q处的凹顶点但始终未碰到边界时，另一组人员在后续疏散过程中一定会在点T处发现该边界.

当疏散区域边界为非凸(凹)多边形时，可采用与凸多边形竞争比类似的分析方法.在分析竞争比时，使Soffline的长度尽可能小，而Sonline的长度则尽可能大，这样计算出的竞争比才能真正体现“最坏”情形.如图4所示，一组受灾人员沿横坐标向右移动单位长度d，然后沿逆时针方向移动一个半圆弧长，并再次到达横坐标，完成了一次半圆移动.接着，再走一段单位长度d，并按逆时针方向移动一个半圆，又一次回到横坐标轴上，完成了第2次半圆曲线移动,其中半圆的半径长度采用双倍策略递增，并且这些半圆共用一个圆心点O.与此同时，另一组人员始终沿着与上一组人员的相反疏散方向进行疏散，直到发现凹多边形P的边界.当点T在S(O，B)内时，Soffline的长度接近于第一个圆的半径时是最优的，即凹点无限接近于第一个圆周.可以看出，当T点无限接近于B点时，各组人员的疏散路径是最长的，也即Sonline的长度最大.所以，当某组疏散人员在点B处碰到多边形边界(相交于点T)时，计算出的竞争比是最大的.

图4 凹多边形内分组数为2的半圆疏散策略Fig.4 Semicircle evacuation strategy with grouping of2 in concave polygon

若假设某组人员在第n+1次疏散时碰到多边形边界，完成疏散，则Dopt是第n个圆周的半径长度，所以竞争比可按如下方法计算：

通过计算半圆疏散策略的竞争比计算，说明半圆策略是解决凹多边形疏散问题的一个高效可行方法.

3 算法的实现

上述算法已通过程序实现.针对不同疏散策略，计算出不同顶点数的多边形的探索路径长度，并计算出竞争比，以便对比分析，如表1所示.其中(凸)与(凹)表示多边形的形状，P表示疏散人员所探索的不同顶点数的多边形，即不同形状的多边形.

算法的有效性是通过竞争比来衡量的，竞争比越低算法越有效.关于凸多边形的问题，文献[14]提出了单源点单组半圆疏散算法，但本文的单源点单组三角形疏散策略却得到了一个更低的竞争比，改进了凸多边形情形下的疏散问题求解算法.针对非凸多边形情形下的疏散问题，文献[15]提出的两组半方形疏散策略的竞争比不超过24，本文提出的两组半圆疏散算法的竞争比则不超过18.56，与半方形疏散策略相比，半圆策略进一步改进了非凸多边形情形的疏散算法.同时，由表1可知，在不同的多边形疏散区域中，凸多边形情形下的三角形策略的竞争比低于半圆策略，所以三角形疏散算法优于半圆疏散算法；非凸多边形情形下的半圆策略竞争比低于半方形策略，所以半圆疏散算法优于半方形疏散算法.

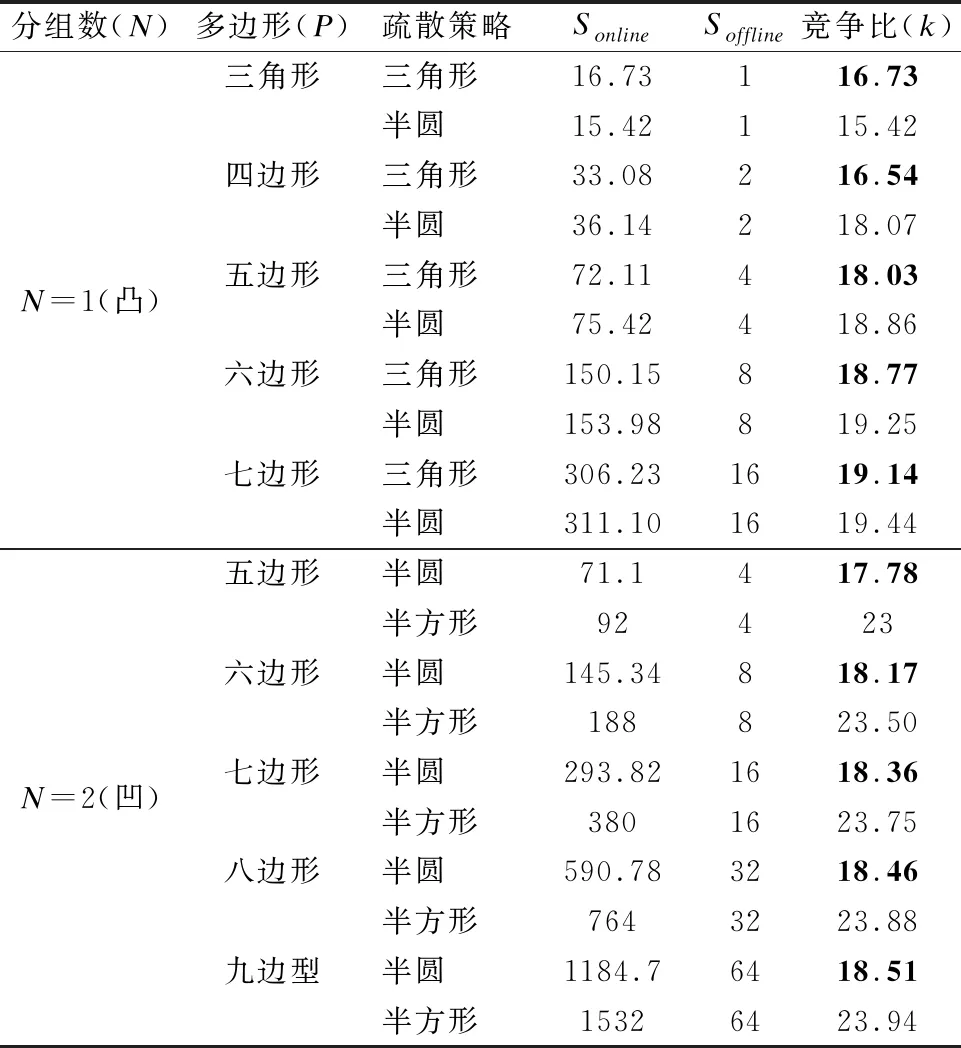
表1 不同疏散策略的实验结果比较Table 1 Comparison of experimental results of differentevacuation strategies

4 结 论

本文主要研究了受灾区域为简单凸多边形和简单非凸多边形情形下单源点疏散问题的疏散策略，其中探索凸多边形区域的单源点单组疏散策略的竞争比为19.48，低于单源点单组半圆疏散策略的19.64[14].由于单组疏散策略只适用于凸多边形区域的问题求解，对于非凸多边形的情形，必须采用多组疏散策略，为此，我们提出了单源点2组半圆疏散策略用于求解非凸多边形的单源点疏散问题，得到了竞争比为18.56的研究结果，优于已有的撤离算法.针对单源点疏散问题的online探索算法，虽然已有一些解决方案，但仍然存在较大的改进空间，需要做进一步研究，以找出更好的疏散方法，获得更低的竞争比，减少疏散成本并方便应用.