基于平均法和多尺度法的输电线舞动解析解精度讨论

刘小会, 杨曙光, 孙测世, 蔡萌琦

(1.重庆交通大学省部共建山区桥梁及隧道工程国家重点实验室， 重庆 400074； 2.重庆交通大学土木工程学院，重庆 400074； 3.成都大学建筑与土木工程学院， 成都 610106)

输电导线覆冰后，横断面由圆形变成新月形、D形和扇形等非圆形截面。由于风对覆冰输电导线施加的竖直向气动力破坏了原有的平衡状态，输电线会发生微弱的振动。风持续地给系统输入能量，振动幅值也会逐渐增大，最终输电导线自身结构阻尼、恢复力和空气动力之间相互调节使得输电导线产生恒定频率和恒定振幅的周期运动，达到一个新的稳态平衡形成舞动。输电线舞动的3个主要影响因素：导线的自身结构、导线覆冰情况以及风的影响。在纬度较高和海拔较高的寒冷地带，由于存在雾凇、雪凇以及复杂的地理环境，输电导线在这种条件下极易覆冰且发生舞动[1]。舞动会使输电导线产生交变的应力，降低输电导线的抗疲劳极限，并且输电导线在长时间断舞动的情况下，容易导致断线事故的发生；同时也容易使得绝缘子串、金具和输电塔产生疲劳损伤甚至破坏。为了使得输电导线能够正常和持久地运行，对覆冰输电导线舞动的研究是十分必要的。

此前，Denhartog[2]提出了垂直舞动机理，研究发现覆冰输电导线舞动横向的幅值远小于竖向幅值，表明舞动主要发生在竖直方向。Rega等[3]分析了面内激励作用下输电导线的高阶摄动解与频响函数的多值响应曲线，然而只是研究了受迫振动并没有考虑导入空气动力荷载。李欣业等[4]对覆冰输电导线考虑了空气动力并研究了环境参数以及结构参数对覆冰输电导线零解稳定性和振幅的影响，但并未考虑输电导线结构自身的非线性。郝淑英等[5]研究了平衡点张力和舞动幅值的改变导致了固有频率的漂移，但并未采用精确程度更高的多尺度法。李黎等[6]采用有限元程序ANSYS建立模型，提出了有效的输电导线舞动的简化分析方法，但并未对模型进行解析解求解分析。黄坤等[7]通过研究非对称截面的弯扭两自由度动力学行为发现由于非线性的影响导致结构的振动幅值会随激励幅值和频率的变化而发生跳跃，但并没给出具体的解析解进行分析。

综上所述，以施加有风激励的非线性覆冰输电线结构为研究对象，用平均法和多尺度法求解出解析解，并对两种解析解的精确度进行讨论。

1 计算和研究模型

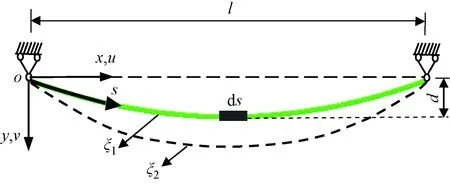
图1 输电导线平面图Fig.1 The plane graph of the transmission conductor

对于平原地区的覆冰输电线，大部分档的导线可近似为等高输电线，因此选取两端固支的等高差单挡输电线为研究对象。在平原地区，高压输电线处于郊外。风主要以层流风为主，所以忽略风的脉动效应，仅考虑稳定风，而且选取最危险工况认为风沿水平方向且与导线的轴向垂直，输电导线平面图如图1所示。输电导线固定支座处于同一水平面，考虑对该系统施加水平风来模拟输电线受风激励的响应。先拟合空气动力系数，然后将空气动力荷载施加于该非线性自治系统中，运用Galerkin方法将覆冰导线舞动的面内偏微分振动方程化简为非线性常微分方程。如图1所示，输电线在重力作用下的平衡状态构形为ξ1，输电导线档距为l，静止状态下输电导线的垂度为d,输电导线自重作用下的线形位于oxy平面上且用函数y来表示，s表示曲线的自然坐标。输电线覆冰后，在风的激励下，输电线会在竖向发生振动，由初始构形ξ1经过一段时间后变化为ξ2，令其变化后的x、y方向上的位移坐标函数分别为u(s,t)、v(s,t)。

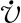
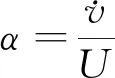
(1)

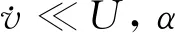
Fy=FLcos(α)+FDsin(α)

(2)

式(2)中：α是一个很小的量，sin(α)≈α，cos(α)≈1，可将式(2)简化为

Fy=FL+αFD

(3)

根据流体诱发振动理论，水平风会使输电导线产生空气升力FL和空气阻力FD[10]，其表达式为

式中：CL为空气升力系数；CD为空气阻力系数。设Cy为水平风对覆冰输电导线竖直向的空气动力系数，将竖直向的空气动力系数Cy进行数值拟合后得到[11]：

Cy=A′α+B′α3

(5)

式(5)中：A′、B′分别为空气动力系数Cy进行数值拟合后的一次项和三次项的动力系数参数。

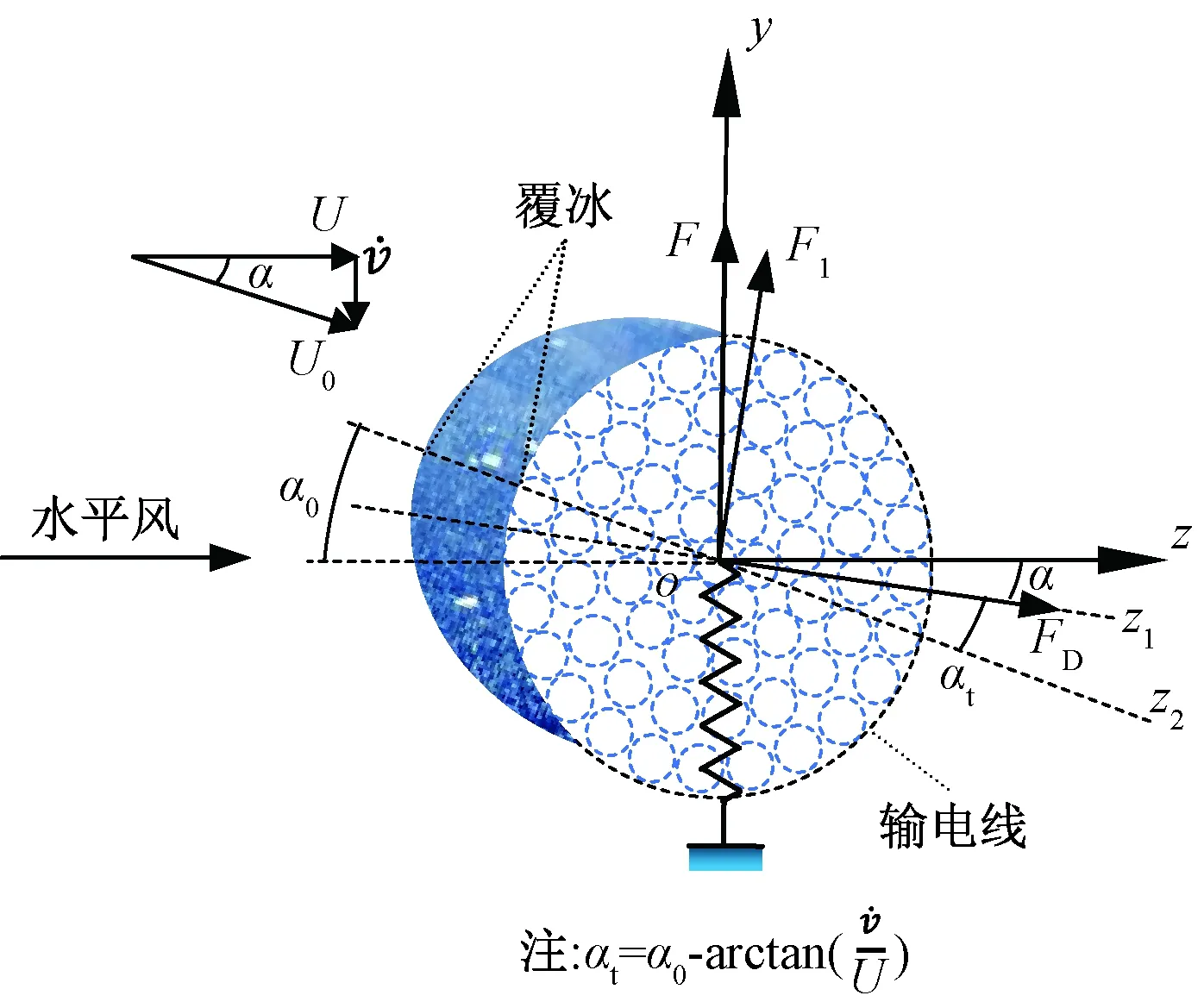
图2 输电导线横截面图Fig.2 The cross section view of a transmission conductor

则风对输电导线产生的竖向作用力Fy为

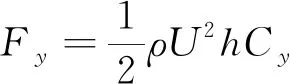
(6)

将式(1)和式(5)代入式(6)中得到竖直向作用力的另一种表达式为

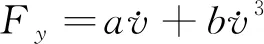
(7)

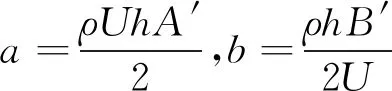
(8)

式(8)中：ρ、h分别为空气密度和输电线的直径，输电线属于大跨度的柔性索结构，针对这种类型的结构，作如下假设：

(1)在静止状态下，输电导线外形可以通过抛物线y=4d[x/l-(x/l)2]来描述。

(2)假设其中ds≈dx，即初始张力的水平分量为导线的张力H。

根据图1，导线面内竖向的运动平衡方程[3]为

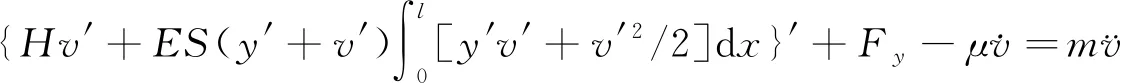
(9)

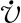
v(x,t)=f(x)q(t)

(10)

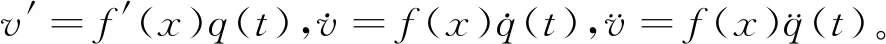
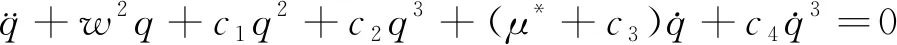
(11)

式(11)中：

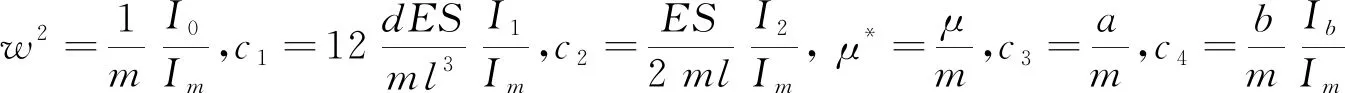
(12)

式(12)中：w对应于输电导线的频率；I的值依赖于特征函数f(x)，定义为

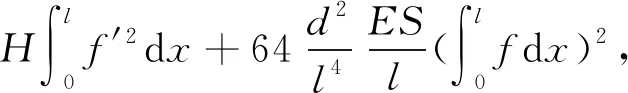
(13)

在式(11)中，由于恢复力中包括二次项和三次项，系统中空气动力荷载的空气动力系数也包含了一次项和三次项，通常认为阻尼和非线性项对系统的影响较小，或针对限幅振动，可以对阻尼项和非线性项作如下转换:

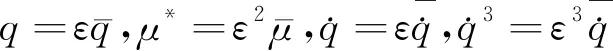
(14)

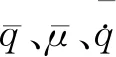
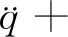
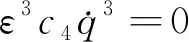
(15)

2 平均法求解

平均法能够一次得到近似解，在工程中常被使用。相比较于Linz Ted-Poincaré法(L-P)、谐波平衡法、Krylov-Bogoliubov-Mitropol’skii法(KBM)、多尺度法和平均法计算简单。平均法设定阻尼项以及非线性项的小量均设为一阶[12]，故非线性常微分方程[式(11)]应该写为

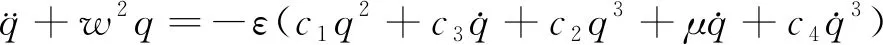
(16)

式(16)表示一个弱非线性自治系统，假设ε为足够小的量，式(16)的左边为线性派生系统，其自由振动解为

令ψ=wt+θ，并且将a和θ考虑为随时间变化的函数，a(t)是振幅函数，θ(t)是相移函数。式(17a)对时间t的导数可表示为

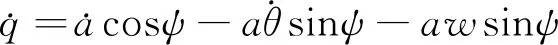
(18)

联立式(17b)与式(18)可得到:

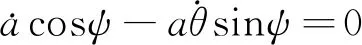
(19)

同理，式(17b)对时间t求导可得：

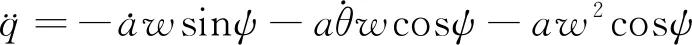
(20)

将式(17)、式(20)代入式(16)得到：

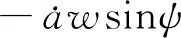
εc1a2cos2ψ+εc2a3cos3ψ-

εc4a3w3sin3ψ=0

(21)

结合式(19)和式(21)解得：

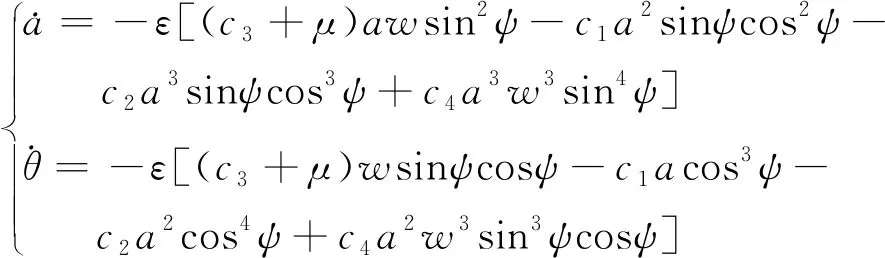
(22)

Q(a,θ)和P(a,θ)表示为

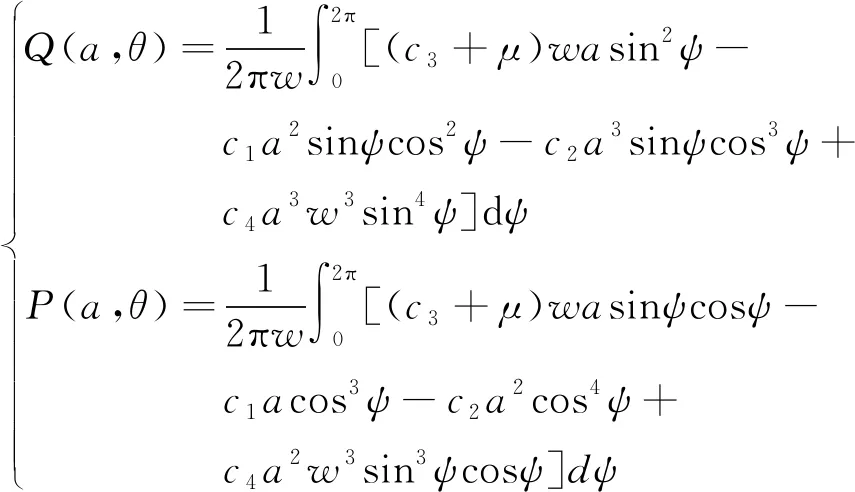
(24)

式(23a)对时间进行积分，可得幅值函数为

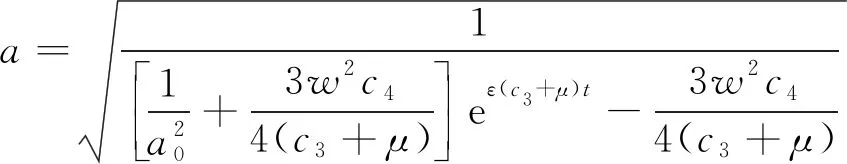
(25)

采用文献[11]的方法，将a看作常值，式(23b)对时间进行积分可得到相移函数为

(26)

综合式(17a)、式(25)和式(26)可得到输电导线竖向振幅表达式为

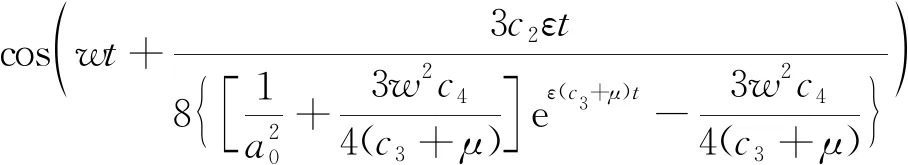
(27)

将式(27)对时间求导数，求得输电导线竖向速度变化规律为

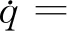
(w+ga2)asin(wt+θ)

(28)

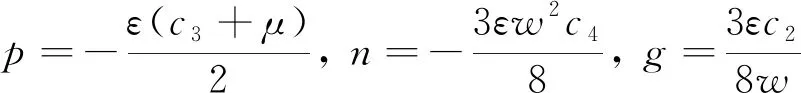
(29)

3 多尺度法求解

多尺度法相比较于平均法能对方程求出更加准确的近似解。采用多尺度法，引入Tn=εnt(n=0,1,…,3)，得到新的独立时间变量，n表示多尺度法划分时间变量的阶数，n取值越大，计算量和复杂程度也会急剧增大[13]，仅考虑多尺度法的三阶近似解。除了多尺度阶数大小对结果有影响外，无量纲参数ε的取值也会影响多尺度最终求得的周期解析解的结果，小量ε越小对弱非线性的近似程度越好，取小量ε=0.1。将q展开ε的幂级数：

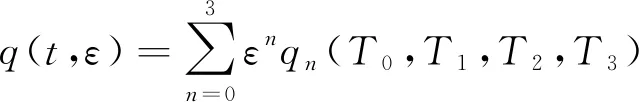
(30)

将式(30)代入式(15)展开得到：

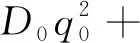
2D0D1q1+w2q2+2c1q0q1+c3(D0q1+

μ(D0q1+D1q0)+c4(D0q0)3]=0

(31)

式(31)中:Dk表示对Tk时间尺度求偏导数，令小量ε的等次幂系数为0，得到如下线性偏微分方程组：

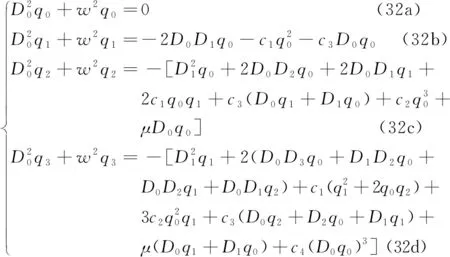
解式(32a)结果为

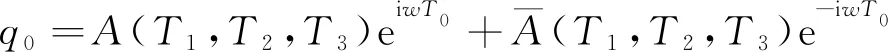
(33)

式(33)中：A可设为

A(T1,T2,T3)=1/2a(T1,T2,T3)exp[iθ(T1,T2,T3)]

(34)

式(34)中：a和θ分别表示系统的振幅和相位。

将式(33)和式(34)代入到式(32b)，D0q0即为q0对时间尺度T0的导数，那么可以得到[14]：

(35a)

(35b)

将式(33)～式(35)代入(32c)中得到：

将式(33)～式(36)代入式(32d)中得到：

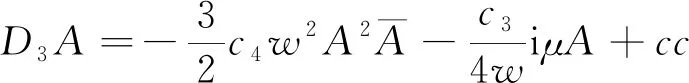
(37)

结合式(34)～式(37)，可得到系统振幅和频率的变化率方程为

(38)

将式(38)对时间积分得到幅值和频率表达式为

结合式(30)、式(33)和式(34)可得到系统ε0阶小量对应的振幅表达式为

q=acosψ

(40)

式(40)中：ψ=wt+θ，结合式(30)、式(33)、式(34)和式(35b)可得到系统(ε0,ε1)阶小量对应的振幅表达式为

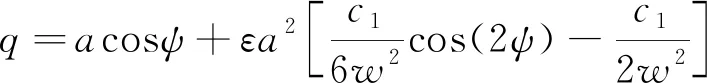
(41)

结合式(30)、式(33)、式(34)、式(35b)和式(36b)可得到系统(ε0,ε1,ε2)阶小量对应的振幅表达式为

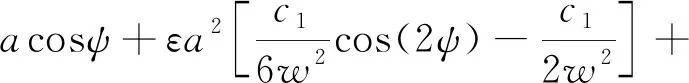
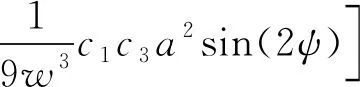
(42)

如上述内容所示，运用多尺度对该弱非线自治方程求解，分别求得幅值、频率表达式以及各阶小量对应的周期解析解。不仅能对风激励下覆冰导线的运动状态进行分析，还能分析各参数对运动状态的影响以及各参数之间相互存在的一些关联，给出了不同阶近似解析解精度讨论。

4 近似解解析精度讨论

4.1 数值解

为了便于分析比较，对于等高差的单挡输电线，覆冰的冰形选用新月形覆冰，选用文献[15]的几何参数、材料参数和相应的气动力参数如表1所示。

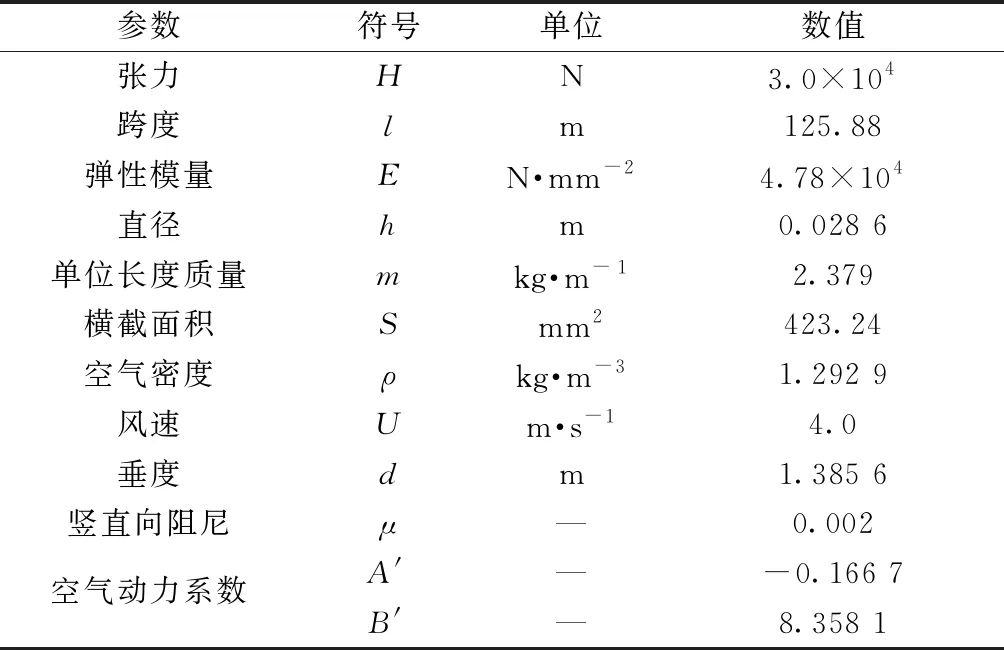
表1 输电导线线路物理参数

为了考查解析解的精度，使用表1中的结构参数和环境参数，让水平风作用在覆冰输电导线上，然后采用Runge-Kutta方法求解式(11)，给输电线施加竖向0.05 m的初始扰动后，用数值方法得到时程位移和速度图像以及相位图[16]。如图3和图4所示，覆冰输电导线在水平风的激励作用下，输电导线的幅值和振动速度随着时间的变化逐渐增大，荷载激励时间达到1 200 s以后，该系统的振幅和振动速度就逐渐趋近于一个稳定的值，数值解的最大幅值分别为0.234 0 m和-0.252 5 m，可见由于系统的非线性项导致了振动中心向下发生了 0.009 25 m 的漂移；速度也逐渐趋近于一个常值，最大竖向速度都趋近于±0.68 m/s。从图3和图4中可看出覆冰输电导线幅值和输电导线速度的变化趋势基本一致。

图5为该弱非线性自治系统的相位图，取输电线受水平风激励后1 800～2 000 s的时段，反映了输电导线在竖直方向上速度和位移的关系图。当到达1 200 s后，幅值和速度趋于常值，就形成如图5的稳定极限环。

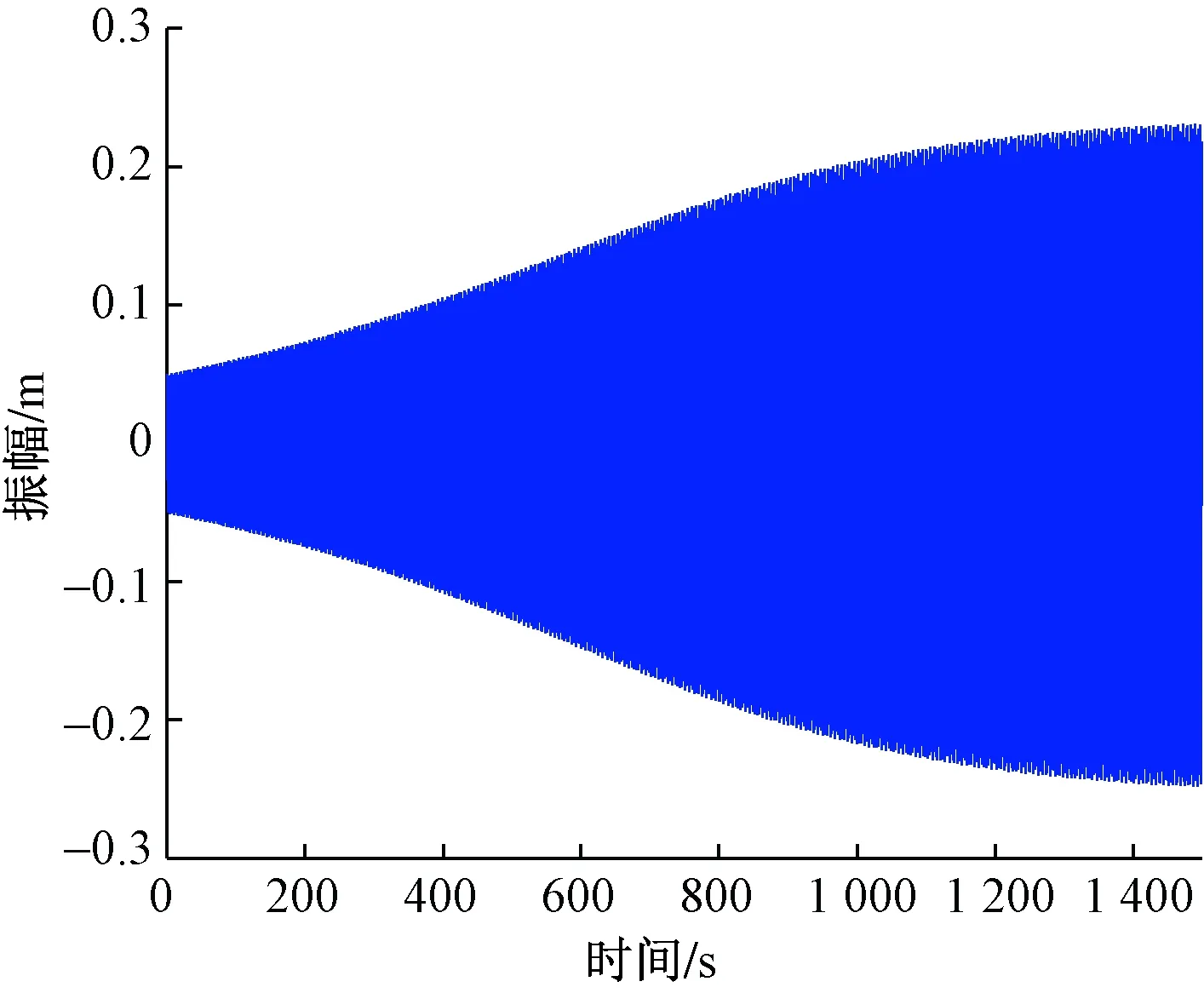
图3 时程位移图像-数值解Fig.3 Time history displacement diagram-numerical solution

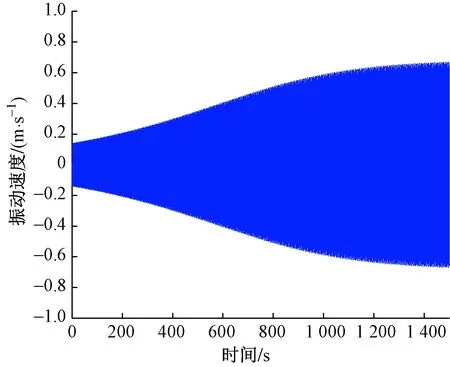
图4 竖向速度图像-数值解Fig.4 Vertical velocity diagram-numerical solution

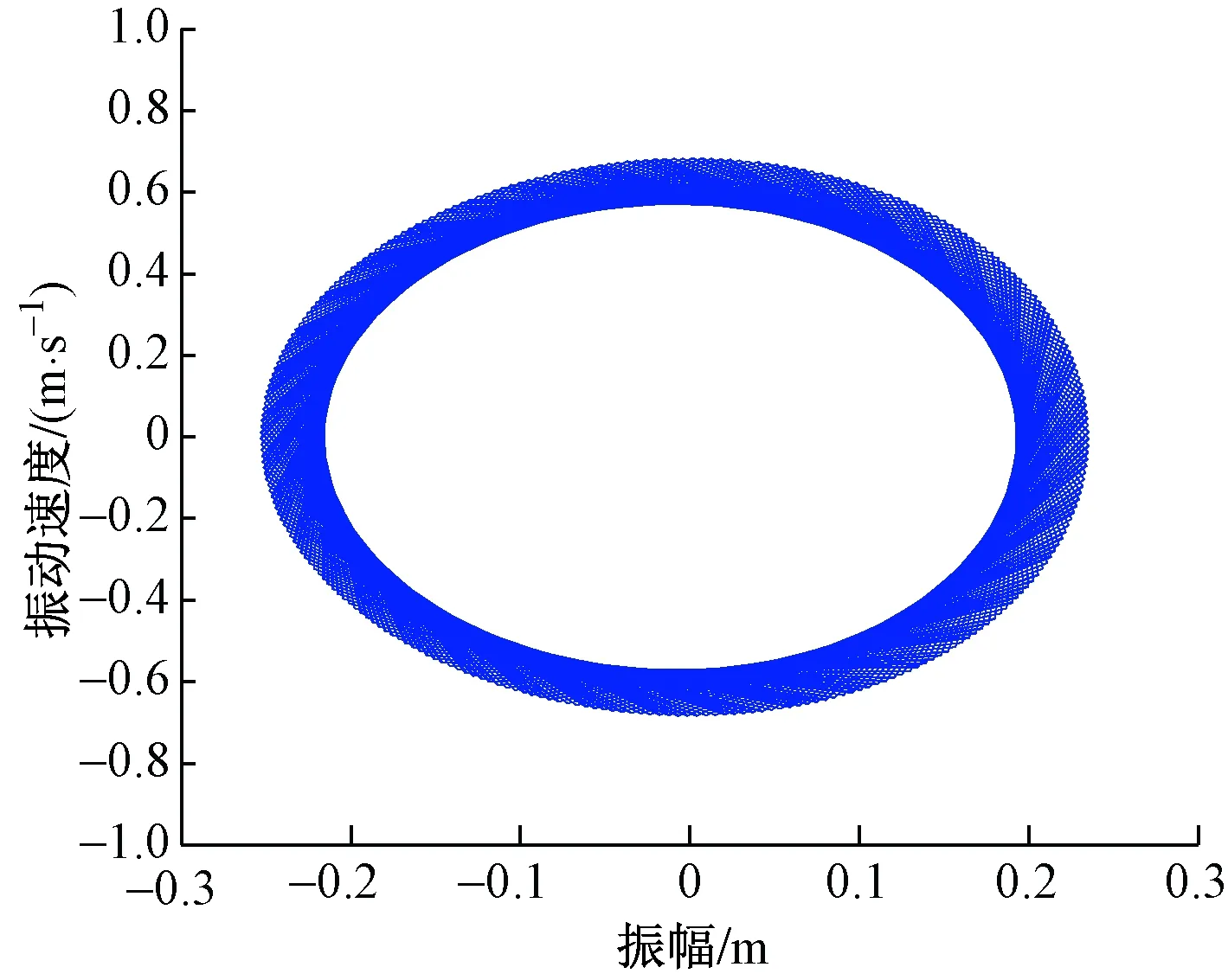
图5 相位图-数值解Fig.5 Phase diagram-numerical solution

4.2 平均法和多尺度法解析解与数值解的比较

平均法和多尺度法都是求解弱非线性问题常用的方法。对于平均法，相比于其他摄动法而言的优点就是能够快速求得近似解；多尺度法的优点就是能够求解更加精确的近似解，可以根据计算精度需要来决定使用几阶小量。小量的阶次越高，计算过程也越复杂，这也是多尺度法的缺点。那么为了讨论这两种方法对于求解覆冰输电线这类弱非线性自治系统的适用性。比较了相同条件下平均法、多尺度法的解析解与数值解结果，得到不同方法的计算结果精确程度。

数值法和平均法时程位移的时间区段如图6所示。从图6可以看出平均法解析解和数值解的图像并不能吻合。造成这种现象的原因是平均法得到的式(26)和多尺度法得到的式(39b)有区别，多尺度法对相位描述的更加准确。当振动方程中含有高次非线性项时，使用平均法对频率的非线性修正项有错误，从而也得到不准确的结果[16]。

图7为平均法解析解与数值法在时间区段内的相位图。图7中坐标为(0,0)的点表示平均法结果的振动中心，坐标为(-0.009 3,0)的点表示数值法结果的振动中心。从图7中看出平均法解析解和数值解的振动中心没有重合，并且两者的相位图也并不能重合。平均法解析解的图像是关于坐标中心对称的，数值方法的相位图则不是关于原点对称，所以结合图6和图7表明平均法的解析解对比数值法结果没有发生漂移现象。图8为式(40)所得结果，仅考虑多尺度法得到的ε0阶对应的解。由图8可以看出多尺度法ε0阶解析解与数值解的最大正向和负向幅值不能完全重合，即表现为振动中心的偏移，与平均法所求结果一致。结合图6～图8和上述分析可以得到：平均法和多尺度法(ε0)的解析解对弱非线性自治系统的振动状态描述不够准确。

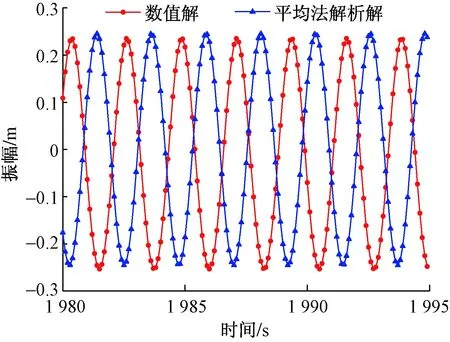
图6 时程位移图-平均法解析解与数值解Fig.6 Time history displacement diagram-average method analytic solution and numerical solution

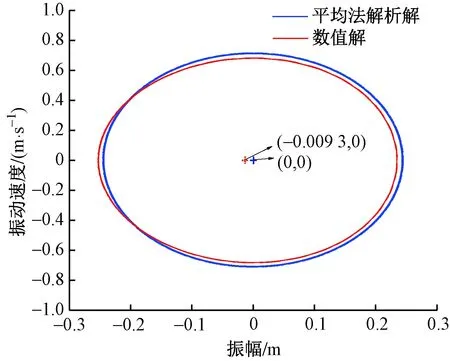
图7 相位图-平均法解析解和数值解Fig.7 Phase diagram-average method analytical solution and numerical solution

图9和图10分别为式(41)和式(42)解析解与数值解对比所得到的结果，其中图9为多尺度法(ε0，ε1)一阶解析解对应的相位图，图10为多尺度法(ε0，ε1，ε2)二阶解析解对应的时程位移图像。从两幅图中可以看出多尺度法(ε0，ε1)和多尺度法(ε0，ε1，ε2)的解析解与数值解图像十分吻合，并且幅值接近，振动中心也发生了漂移现象。图11是多尺度法(ε0，ε1)和多尺度法(ε0，ε1，ε2)解析解对弱非线性系统的振动状态的描述，从图11中可以看出，在此种工况下，多尺度法(ε0，ε1)和多尺度法(ε0，ε1，ε2)解析解均能十分准确地描述系统的相位和幅值。

图8 时程位移图像-多尺度法(ε0)解析解Fig.8 Time-history displacement diagram-multiscale method (ε0) analytic solution

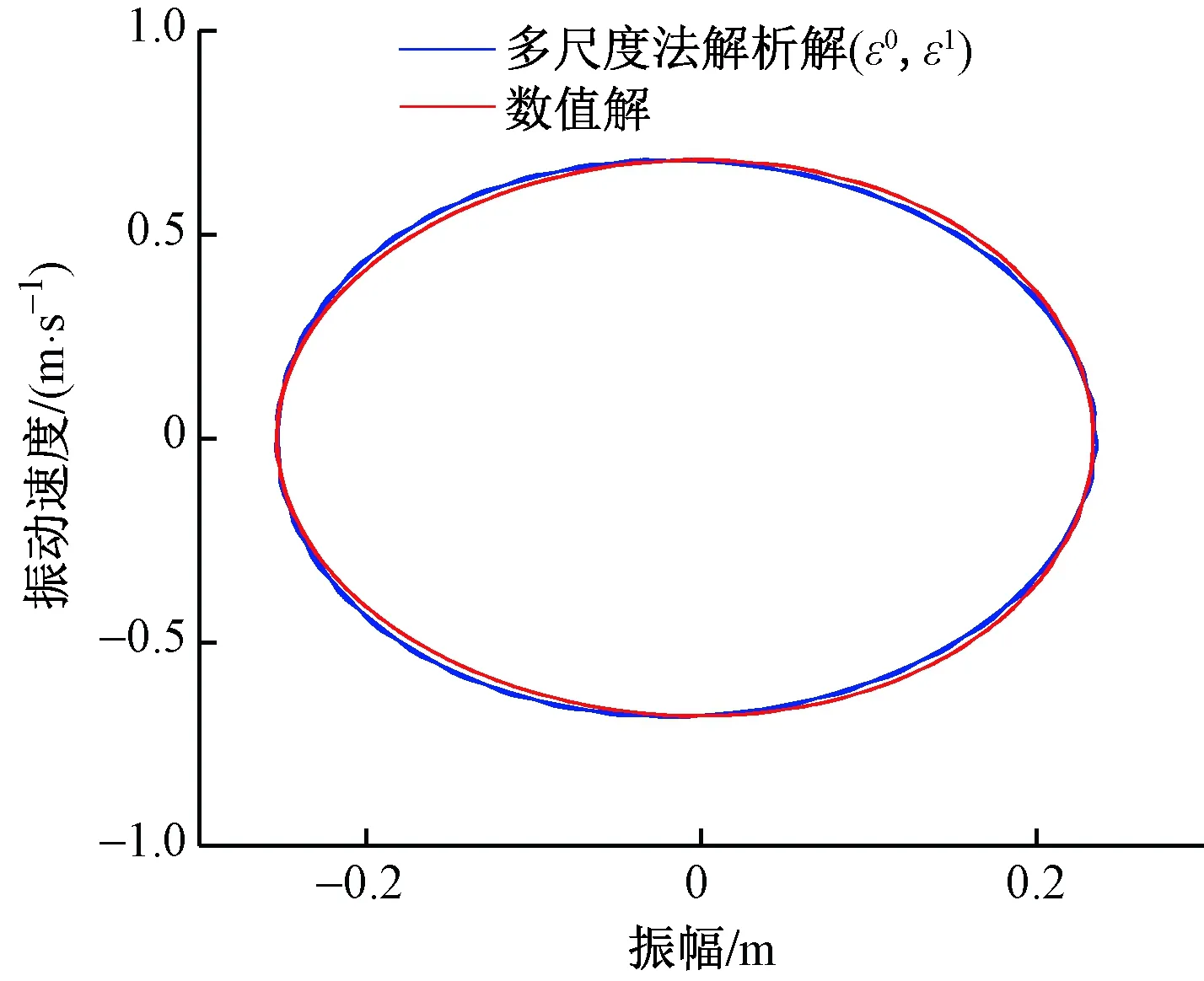
图9 相位图-多尺度法(ε0、ε1)解析解和数值解Fig.9 Phase diagram-multiscale method (ε0，ε1) analytic solution and numerical solution

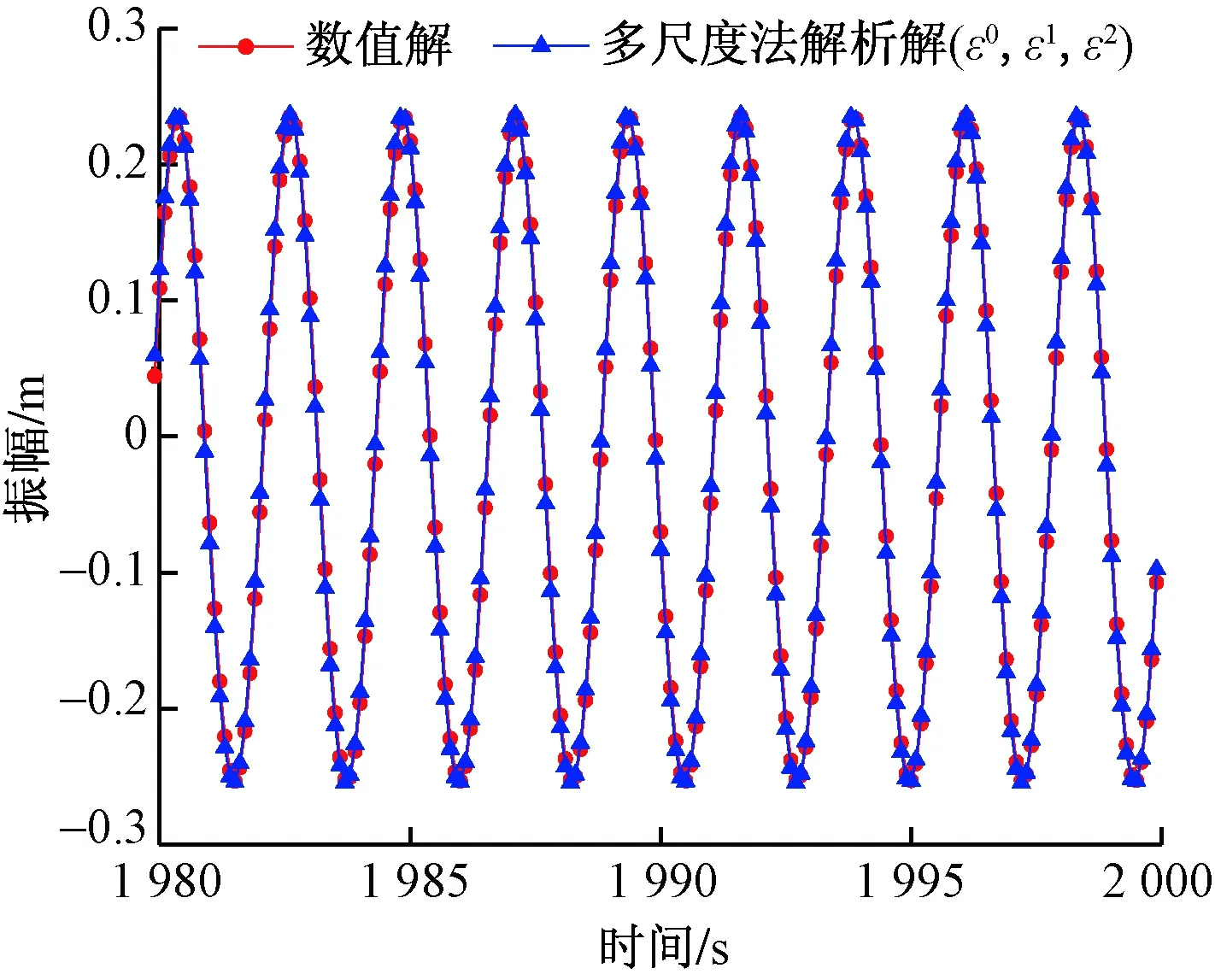
图10 时程位移图像-多尺度法(ε0，ε1，ε2)解析解和数值解Fig.10 Time-history displacement diagram-multiscale method (ε0，ε1，ε2) analytic solution and numerical solution

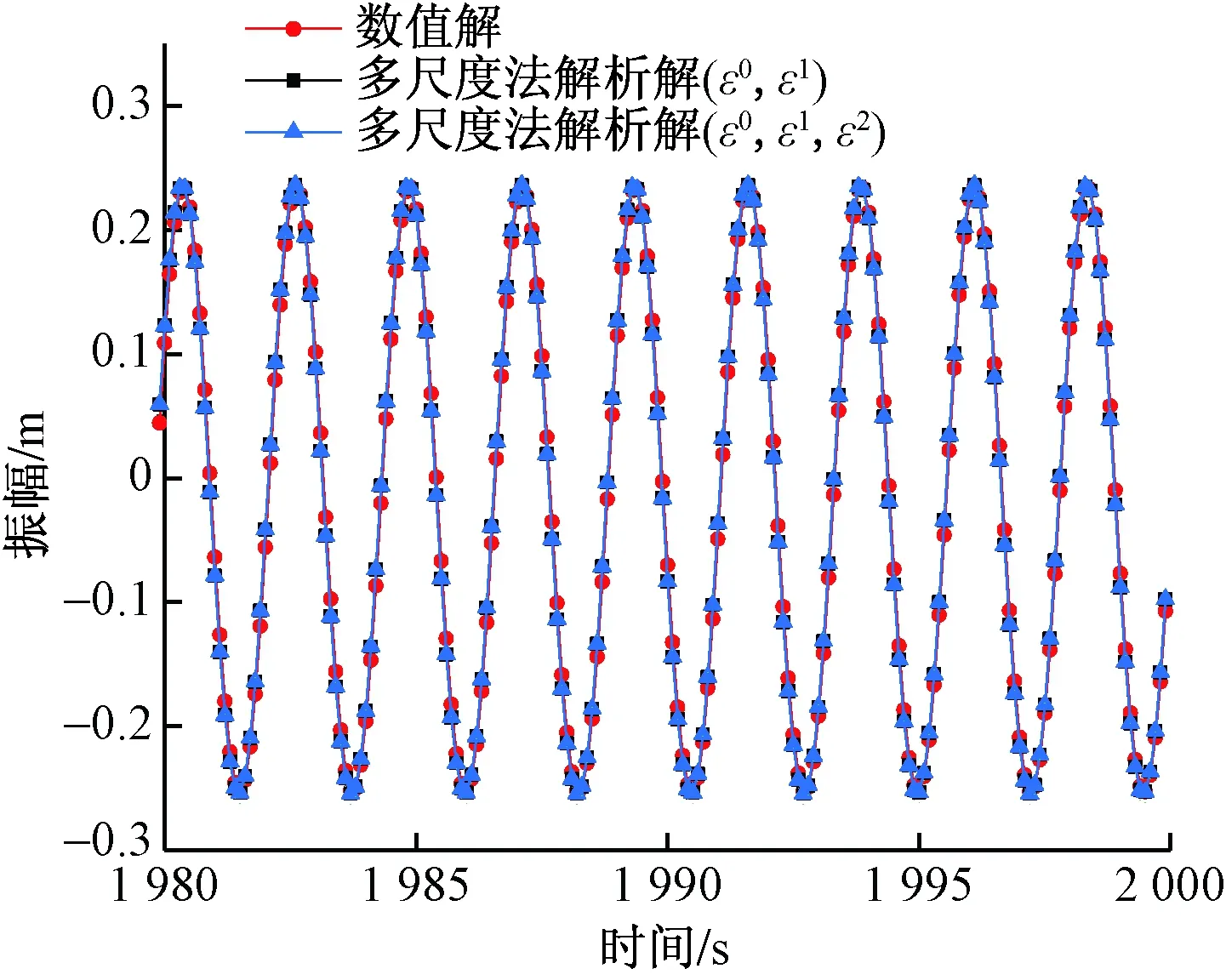
图11 时程位移图像-多尺度法(ε0，ε1)(ε0，ε1，ε2)解析解和数值解Fig.11 Time-history displacement diagram-multiscale method (ε0，ε1)(ε0，ε1，ε2) analytical solutions and numerical solution

为了进一步分析平均法、多尺度法的精度，将舞动的幅值与数值解进行差异性分析，如表2所示。

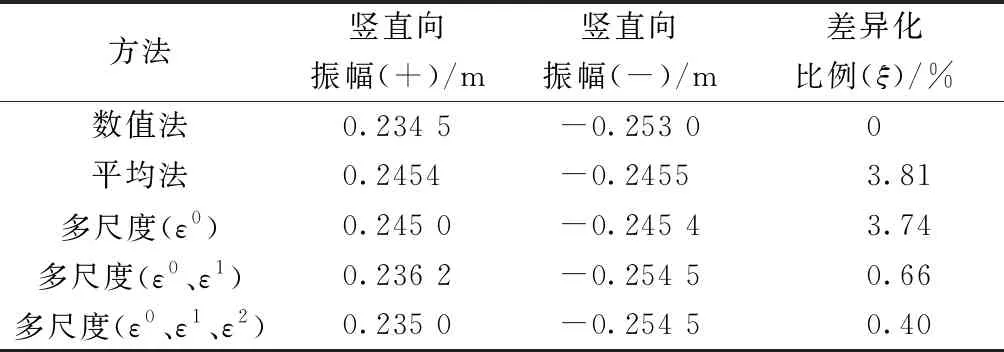
表2 解析解-数值解

表2中数据进一步证明了运用平均法和多尺度(ε0)求解该弱非线性自治系统的周期解与数值法有一定的差异，采用二阶(ε0，ε1，ε2)多尺度法对应的解析解能对弱非线性系统进行更为准确的描述。

4.3 风速对振幅的影响

覆冰输电导线舞动受导线的自身结构、导线覆冰情况以及风的影响。一般情况下，输电线发生舞动后幅值和振动速度随着风速的提高而增大。而弱非线性系统以自身的运动状态作为调节器[17]，因此风速对输电线舞动有比较大的影响。为了能确定风速的增大会不会对多尺度法周期解析解的准确性有影响，以下研究不同风速对多尺度法和平均法解析解精度的影响。

图12为风速10 m/s时舞动位移时程曲线，输电导线振幅随着时间增长较为缓慢，到达700 s时振幅才逐渐稳定；并且当输电导线发生舞动时，输电导线幅值为0.596 0 m和 -0.726 0 m。图13为风速16 m/s时的图像，输电导线发生舞动时间缩减至450 s;舞动幅值也增大到0.918 0 m和-1.258 8 m。上述分析可以得出风速的增大会使得覆冰输电线发生舞动所需要的时间减少，并且舞动幅值和速度也会增大。

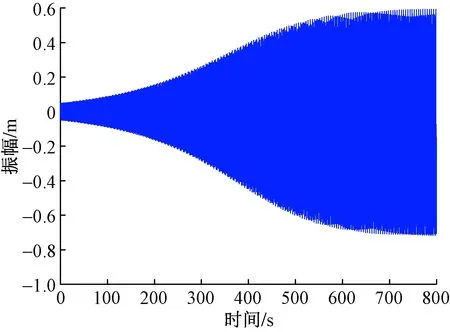
图12 风速为10 m/s的时程位移图像Fig.12 Time history displacement diagram with wind speed is 10 m/s

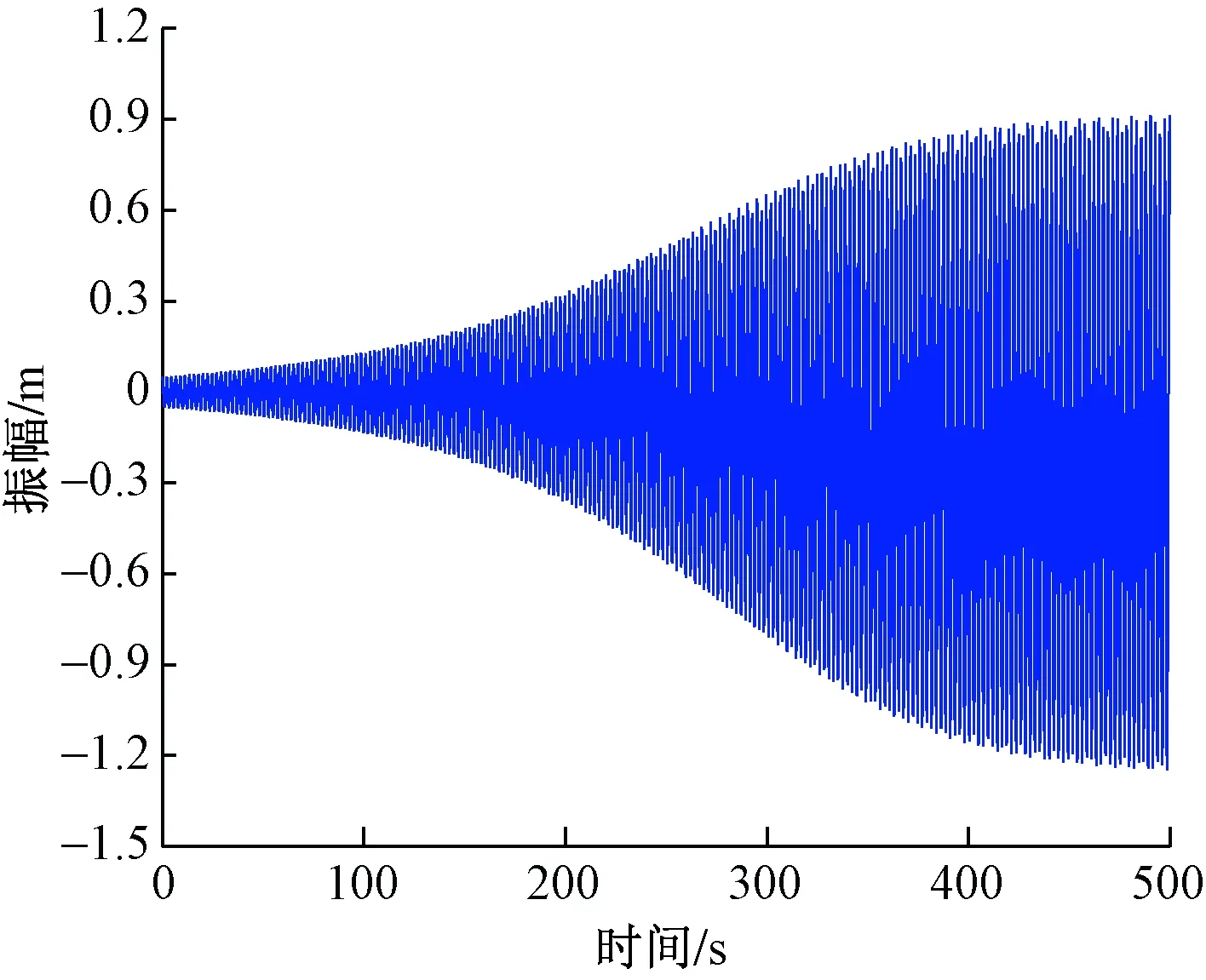
图13 风速为16 m/s的时程位移图像Fig.13 Time history displacement diagram with wind speed of 16 m/s

为了弄清楚幅值变化对漂移量的影响，采用数值方法，取4～20 m/s的风速得到振幅和漂移量随风速变化的具体情况，结果如表3所示。表3中主要包括竖直向的最大正向位移和最大负向位移，以及振动中心的漂移量。可以看出，随着风速的增加，不仅舞动幅值会逐渐增加，振动中心的漂移量也会随着增加。舞动幅值从风速为4 m/s的 0.243 3 m 到风速为20 m/s的1.384 3 m。振动中心漂移量也从风速4 m/s的0.009 3 m到风速 20 m/s 的0.264 8 m。表3可以明显看出，振幅增长和风速是正相关的。风速的增大也使得输电导线舞动的振动中心漂移量增加。舞动振幅是不会一直增长的，当输电导线振幅达到限值时，可能会发生金具损坏或断线等危害。

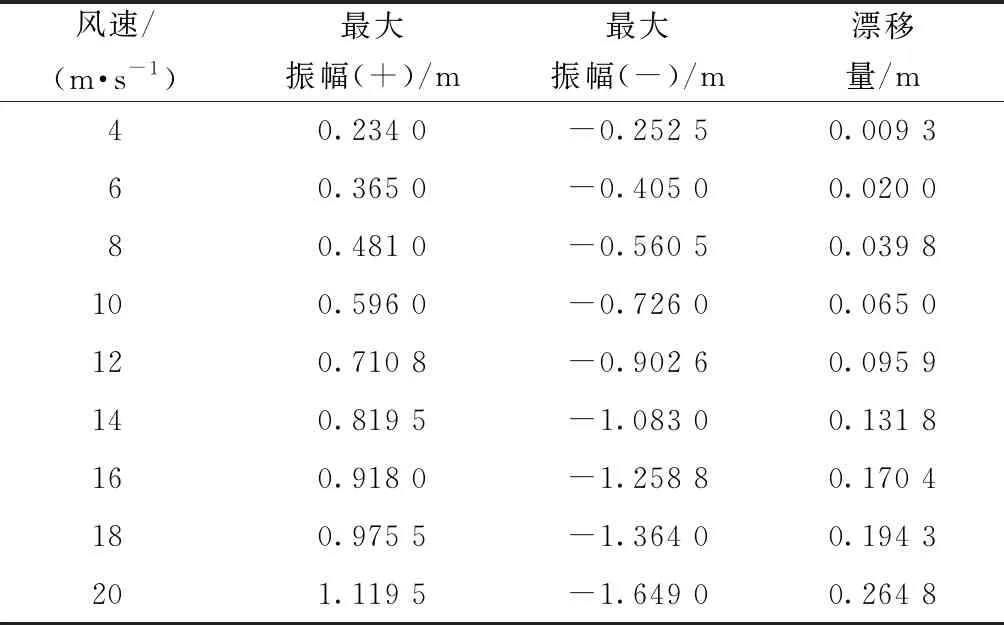
表3 数值解

随着风速的改变，为了检验平均法和多尺度法解析解之间的误差是否有变化，将平均法和多尺度法对应的零阶、一阶、二阶解析解分别和数值解作对比分析，得到的误差如表4所示。从表4中可清楚地看出，随着风速的增大，各方法的误差也随着增大，其中平均法和多尺度零阶的误差变得更大(从4 m/s的3.8%到20 m/s的19.2%)。而多尺度法二阶对应的解析解在风速达到20 m/s时，误差仅为3.3%。因此，相较于平均法和多尺度法零阶小量对应的周期解析解，多尺度一阶(ε0，ε1)解析解以及多尺度二阶(ε0，ε1，ε2)解析解适用于描述输电导线舞动过程，并且后者的描述更加准确。

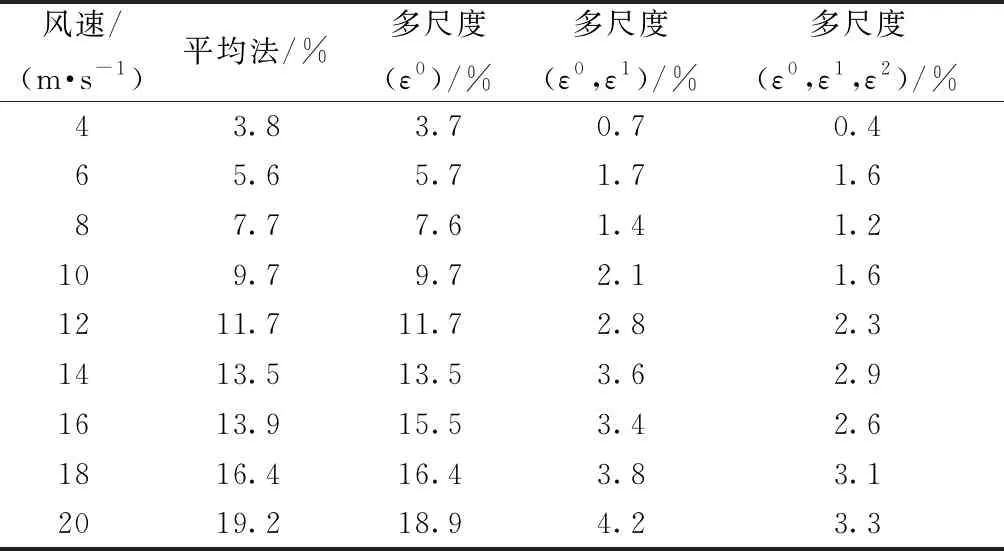
表4 风速变化对解析解误差的影响

5 结论

运用平均法和多尺度法求解出该弱非线性舞动方程的振幅和相位解析解，然后用数值方法求得数值解，将解析解和数值解进行比较得到如下结果。

(1)将平均法和多尺度ε0阶解析解与数值解进行比较，得出平均法和多尺度法ε0阶解析解精度很接近，但是平均法不能准确描述相位的变化情况，而多尺度法ε0阶解析解对相位的描述有较高的精度。

(2)由于非线性项的存在，覆冰输电线舞动的振动中心会发生漂移，并且随着风速的增大振动中心漂移量也逐渐增加。

(3)随着风速的增加，非线性逐渐加强，运用平均法和多尺度法ε0阶解析解结果的误差显著增加，误差最大达到19.2%，因此不适于描述非线性舞动过程，多尺度一阶(ε0，ε1)解析解以及多尺度二阶(ε0，ε1，ε2)解析解误差逐渐增大，但是误差最大仅为4.2%，仍可以较为准确描述舞动幅值。