平面几何历史“名题”视角下的解析几何
沈海全 裘孟超
(1.浙江省绍兴市越州中学 312000;2.浙江省嵊州市城关中学 312400)
在解析几何教学中,常常有教师把“解析几何教学”仅简单地理解为“用坐标法求解几何问题”,因而,常常忽视对其作为几何图形的特征和性质的分析,忽视几何方法的运用.其实,解析几何的建立是数与形有机结合的标志,是数形结合、运动变化、转化化归思想的集中体现,有的解析几何问题还蕴含丰富的平面几何历史“名题”背景,如“圆幂定理”、“燕尾定理”、“蝴蝶定理”、“梅涅劳斯定理”、“托勒密定理”等. 笔者认为,解析几何教学除了“坐标法”思想外,也要重视引导学生从平面几何的视角分析,重视运用平面几何知识,做到几何方法与代数方法的有机结合,甚至还可以挖掘问题所蕴含的平面几何历史“名题”背景.下面笔者结合实例谈谈解析几何中的平面几何历史“名题”,供读者赏析,不当之处请读者斧正.
一、解析几何中的“圆幂定理”
圆幂定理若过定点P作一动直线与半径为R的圆O相交于A,B两点,则PA·PB=|OP2-R2|(把常数|OP2-R2|叫做定点P对于定圆O的幂).
圆幂定理是一个总结性的定理,是对相交弦定理、切割线定理以及它们推论的统一与归纳,证明如下.
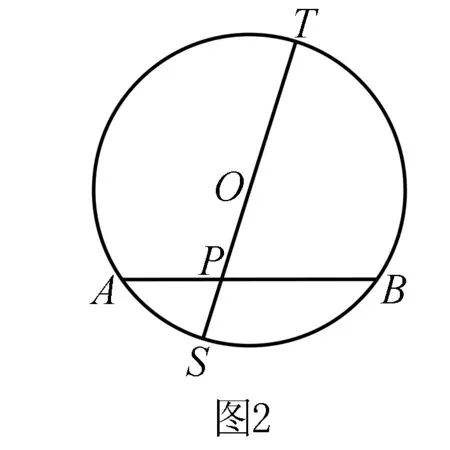
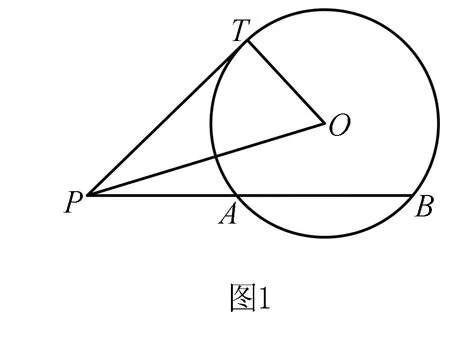
证明当点P在圆O外时,如图1所示,过P作圆O的切线PT,由切割线定理及勾股定理可得PA·PB=PT2=OP2-R2;当点P在圆O上时,不妨设P与A重合,易得PA·PB=0=OP2-R2;当点P在圆O内时,如图2所示,过P作圆O的直径ST,由相交弦定理可得PA·PB=PS·PT=(R-OP)(R+OP)=R2-OP2.
综上PA·PB=|OP2-R2|,证毕.
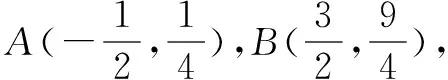
(1)求直线AP斜率的取值范围;
(2)求|PA|·|PQ|的最大值.
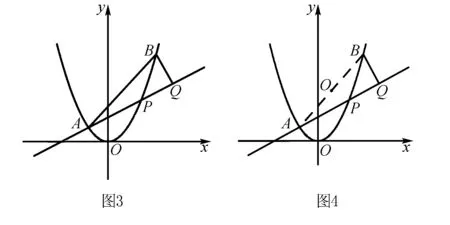
解(1)限于篇幅,略.
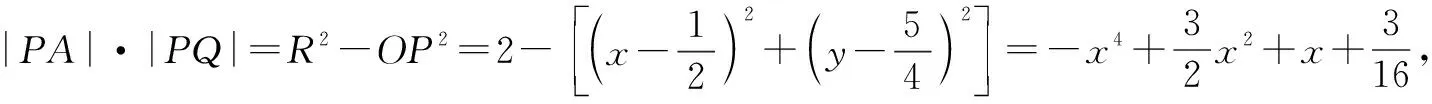
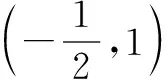
评注本题秉承了浙江试题的特色,素材朴素,内涵丰富,较宽的切入口给不同层次的学生提供了思考的空间,但方法不当会计算量较大耗时较多甚至很难解出来. 实际上本题命题者以抛物线为载体,以平面几何历史名题“圆幂定理”而命制的试题,若能从本题几何背景即圆幂定理入手,可发现解法新颖别致、赏心悦目.
二、解析几何中的“燕尾定理”
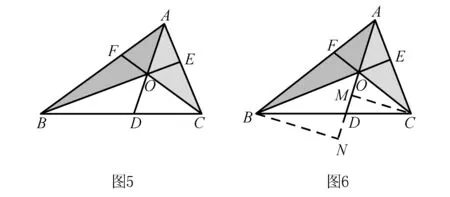
燕尾定理如图5在△ABC中,AD,BE,CF相交于同一点O,那么S△ABO∶S△ACO=BD∶DC.
燕尾定理将三角形的面积比转化为线段长度比,因为△ABO,△ACO的图形形状很像燕子的尾巴,所以这个定理被称为燕尾定理.该定理在许多几何题目中都有着广泛的运用,为三角形面积比与对应的底边比提供了互相联系的途径.
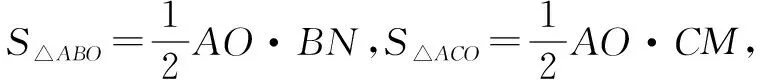
试题赏析(2019浙江高考第21题)如图7,过焦点F(1,0)的直线与抛物线y2=2px(p>0)交于A,B两点,点C在抛物线上,△ABC的重心G在x轴上,直线AC交x轴于点Q(点Q在点F右侧).
(1)求抛物线的方程及准线方程;
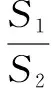
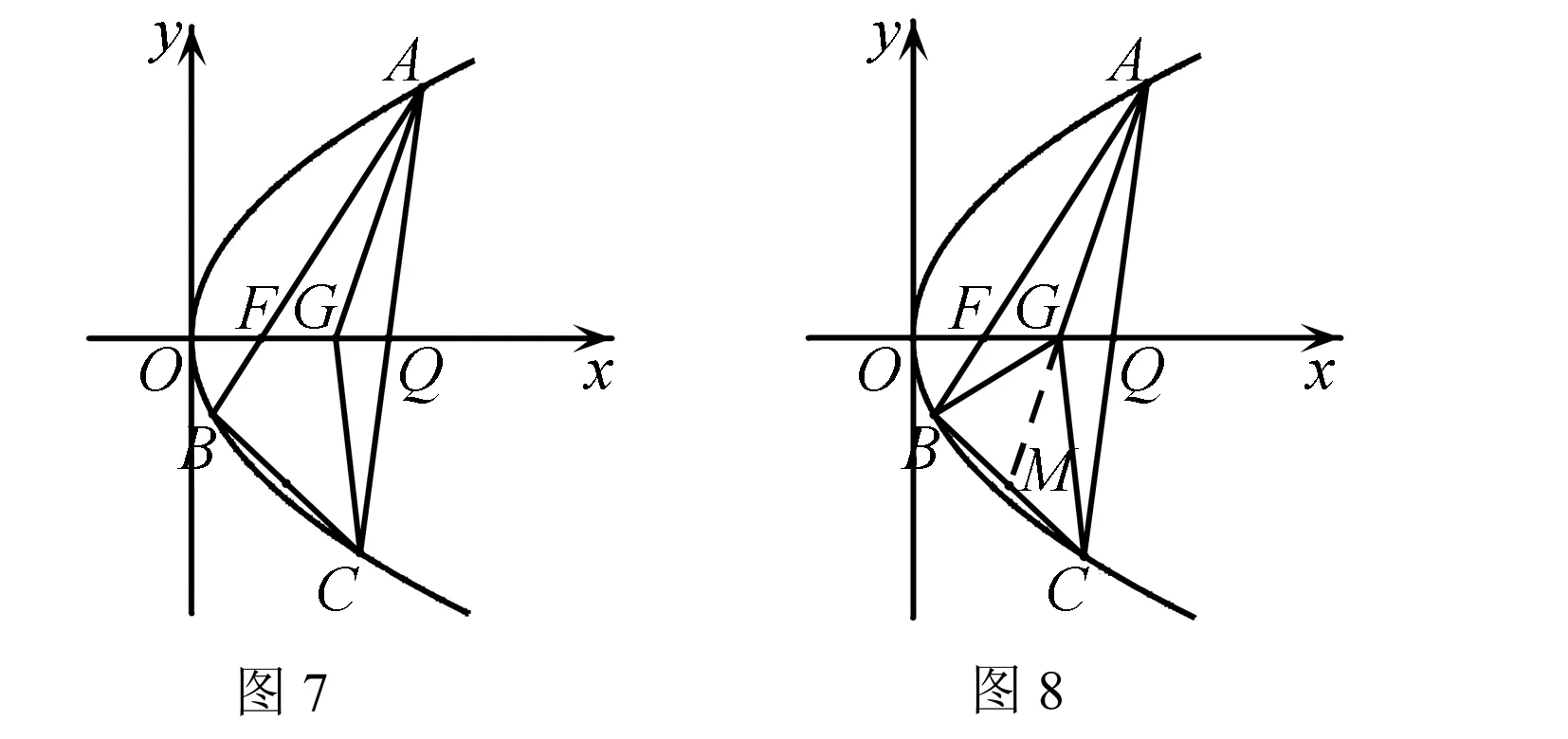
解(1)限于篇幅,略.
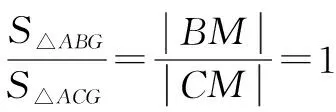
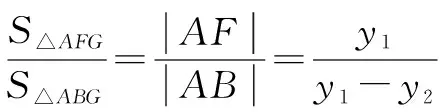
又注意到,y3=-(y1+y2)④,
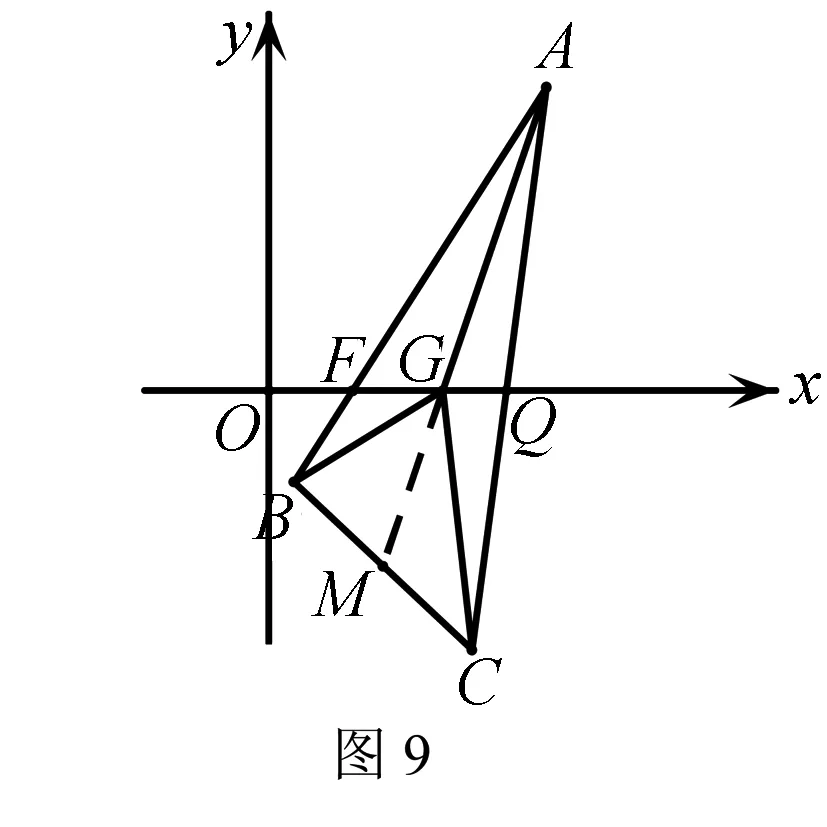
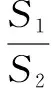
评注命题者以抛物线为载体,平面几何历史“名题”燕尾定理为几何背景而命制解析几何试题,考试院给出的答案是利用点参数来表示面积之比从而求得最小值,利用“坐标法”思想须较强的运算功底.但若利用燕尾定理将面积之比转化为线段长度之比,从而很快可用点坐标表示(即数与形的有机结合),有效避开了设点求其他点的过程,大大减少运算量.更可贵的是挖掘了试题的本质,站到了命题者的高度.
三、解析几何中的“蝴蝶定理”
蝴蝶定理如图10,设AB是已知圆的弦,M是AB的中点,弦CD,EF过点M,弦CF,ED与AB分别相交于P,Q两点,求证:PM=MQ.
以上问题的图形,像一只在圆中翩翩起舞的蝴蝶,这正是该命题被冠以“蝴蝶定理”美名的缘由.
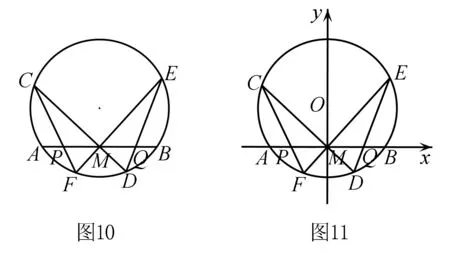
证明(1983单墫教授给出的证明)如图11,以M为原点,弦AB所在直线为x轴,视圆O为单位圆,建立直角坐标系.设圆O的方程为x2+(y-a)2=1,直线的方程分别为y=k1x,y=k2x,由圆和直线组成的二次曲线系方程为μ[x2+(y-a)2-1]+λ(y-k1x)(y-k2x)=0.令y=0,则xP,xQ满足方程(μ+λk1k2)x2+μ(a2-1)=0,由于x的系数为0,结合韦达定理可得xP+xQ=0,即xP=-xQ,故PM=MQ.
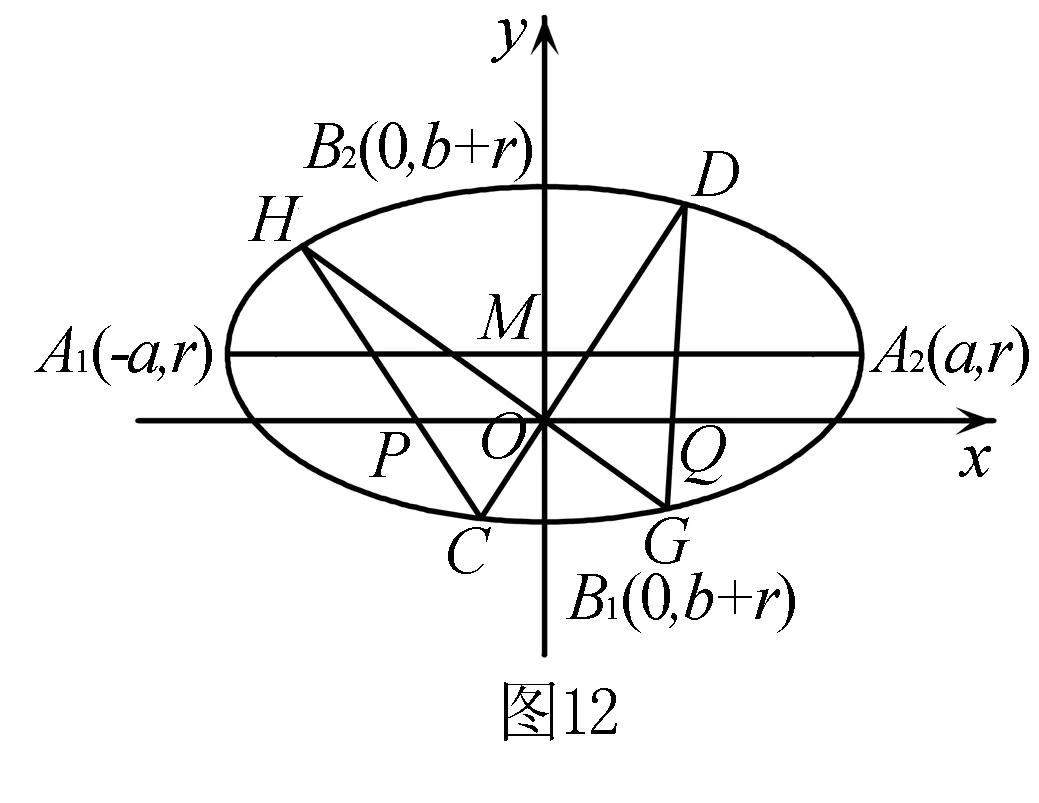
试题赏析(2003年北京理科高考18题)如图12,已知椭圆的长轴A1A2与x轴平行,短轴B1B2在y轴上,中心M(0,r)(b>r>0).
(1)写出椭圆方程并求出焦点坐标和离心率;
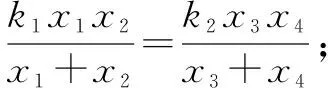
(3)对于(2)中的点C,D,G,H,设CH交x轴于P点,GD交x轴于Q点,求证:|OP|=|OQ|.(证明过程不考虑CH或GD垂直于x轴的情形).
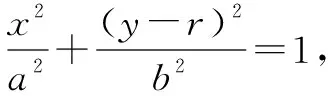
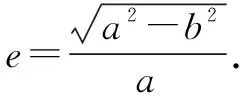
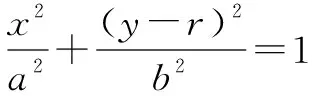
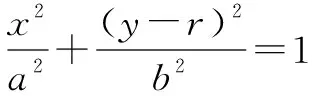
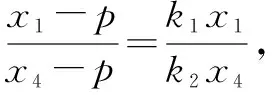
所以|p|=|q|,即|OP|=|OQ|.
评注高考命题者将这只“蝴蝶”飞入了椭圆,使得问题和图形都显得非常漂亮. 本题实质是蝴蝶定理的推广,是变异了的“蝶形”.下面请看蝴蝶定理的推广,证明同上问题,留给读者证明.
蝴蝶定理推广在圆锥曲线中,过弦AB的中点M作两条弦CD,EF,直线CE和DF交直线AB于点P,Q,则有MP=MQ.
四、解析几何中的“梅涅劳斯定理”
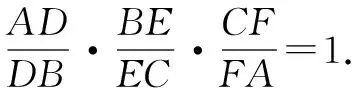
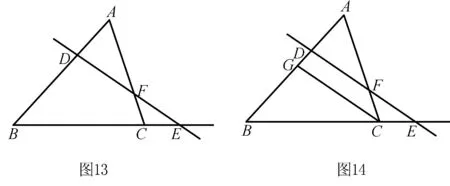
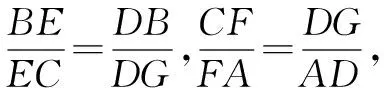
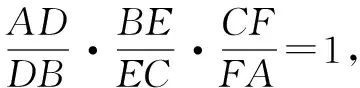
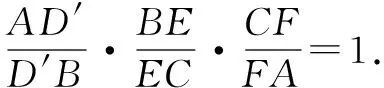
试题赏析(2012年北京理科高考第19题)已知曲线C:(5-m)x2+(m-2)y2=8(m∈R)
(1) 若曲线C是焦点在x轴上的椭圆,求m的取值范围;
(2) 设m=4,曲线C与y轴的交点为A,B(点A位于点B的上方),直线y=kx+4与曲线C交于不同的两点M,N,直线y=1与直线BM交于点G. 求证:A,G,N三点共线 .
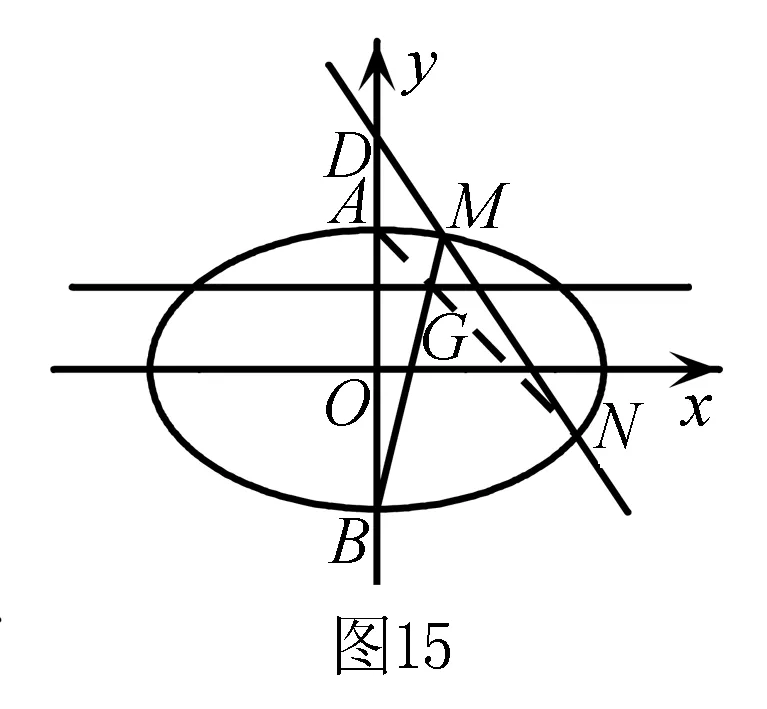
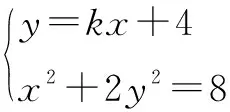

评注命题者以椭圆为载体,以平面几何历史名题“梅涅劳斯定理逆定理”为背景而命制的试题,若能从几何背景入手,解法新颖别致,明显优于利用斜率、向量来证明.
五、解析几何中的“托勒密定理”
托勒密定理在圆内接四边形中,两条对角线的乘积等于两组对边乘积之和.如图16,设四边形ABCD内接于圆O,则有AB·CD+AD·BC=AC·BD.
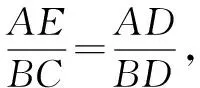
由①+②得AB·CD+AD·BC=AC·BD.
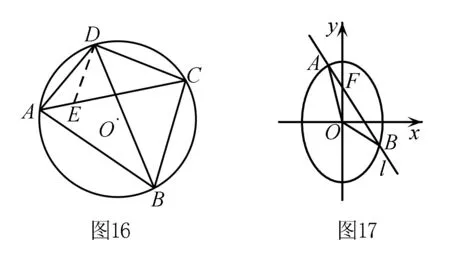
托勒密定理逆定理两组对边乘积之和等于两条对角线之积的凸四边形必内接于圆.
限于篇幅,托勒密定理逆定理留给读者自行证明.
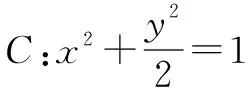
(1)求证:点P在椭圆C上;
(2)设点P关于点O的对称点为Q,求证:A,P,B,Q四点在同一圆上.
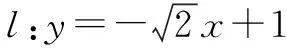
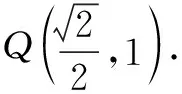
评注命题者以椭圆为载体,以平面几何历史名题“托勒密定理逆定理”为背景而命制的试题,若能从几何背景入手解法新颖别致,明显优于利用方程来证明.
解析几何的核心思想是坐标法,但解析几何的研究对象是“几何图形”,若有时能站在平面几何的视角来观察分析图形,或许会有不一样的风景.

