介质存在时利用镜像法求解电势的讨论

付春娥

(西安交通大学 物理学院 应用物理系，陕西 西安 710049)

若假设在下半空间是充满介电常数为ε的介质，上半空间在(0,0,a)处有一点电荷q，那么在点电荷q产生的电场的作用下，介质将发生极化，在介质的交界面处会出现极化电荷，进而极化电荷产生附加电场，与点电荷q产生的场叠加在一起形成总场.对于此电场的求解，一般采用镜像法[1-5]先求解相应的电势，再得到电场.而镜像法的关键在于，在求解的区域外引入适当的镜像电荷，使镜像电荷与点电荷q形成的场满足边值关系.本文将要讨论的是，在这种情况下，可以引入不同的镜像电荷，而得到同样的电势.

1 在(0,0,a)和(0,0,-a)处引入镜像电荷q′

考虑极化电荷在上半空间的电场，可在下半空间的引入的镜像电荷q′(假设在(0,0,-a)处)，如图1中(a)所示.同时，考虑极化电荷在下半空间的电场，可在上半空间引入的镜像电荷q′(假设在(0,0,a)处)，如图1中(b)图所示.假定这两个镜像电荷的电量相同，进而考虑边值关系来确定它们的带电量.

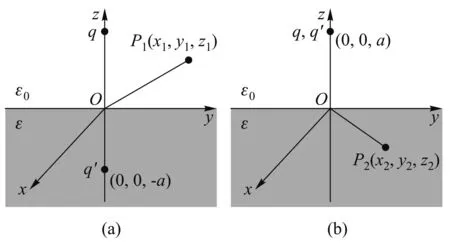
图1 镜像电荷的选择1

建立直角坐标系，引入上述镜像电荷后，在上半空间某一点P1(x1,y1,z1)处的总电势可以表示为

(1)

而在下半空间任意一点P2(x2,y2,z2)的电势为

(2)

(3)

所以叠加得上半空间任意一点(x1,y1,z1)及下半空间中任意一点(x2,y2,z2)的电势为

(4)

(5)

注意：在求下半空间的电势时，此处用了真空中的介电常数，而不是介质中的介电常数.而由表达式(2)可以进一步理解为，在下半空间的场是由在(0,0,a)处的总电量为

(6)

其镜像电荷在真空中产生的电场为式(5).因此也可以将这种镜像电荷称为真空中的镜像电荷，它所代替的是自由电荷与界面上的束缚电荷在下半空间的作用.

2 在(0,0,a)和(0,0,-a)处引入镜像电荷q′及q″

下面给出另一种镜像电荷的引入方法，可以得到与式(4)、(5)相同的场分布.

首先，如果仍假设在上半空间的电场由自由电荷及下半空空间(0,0,-a)处引入的镜像电荷q′产生的场叠加而成，如图1中(a)图所示.那么在上半空间某一点P1(x1,y1,z1)处的总电势可以表示为

(7)

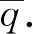
那么下半空间任意一点P2(x2,y2,z2)的电势为

(8)

由边值关系最后可得

(9)

而此时空间中的电势与用第一种方法求得的完全一致.

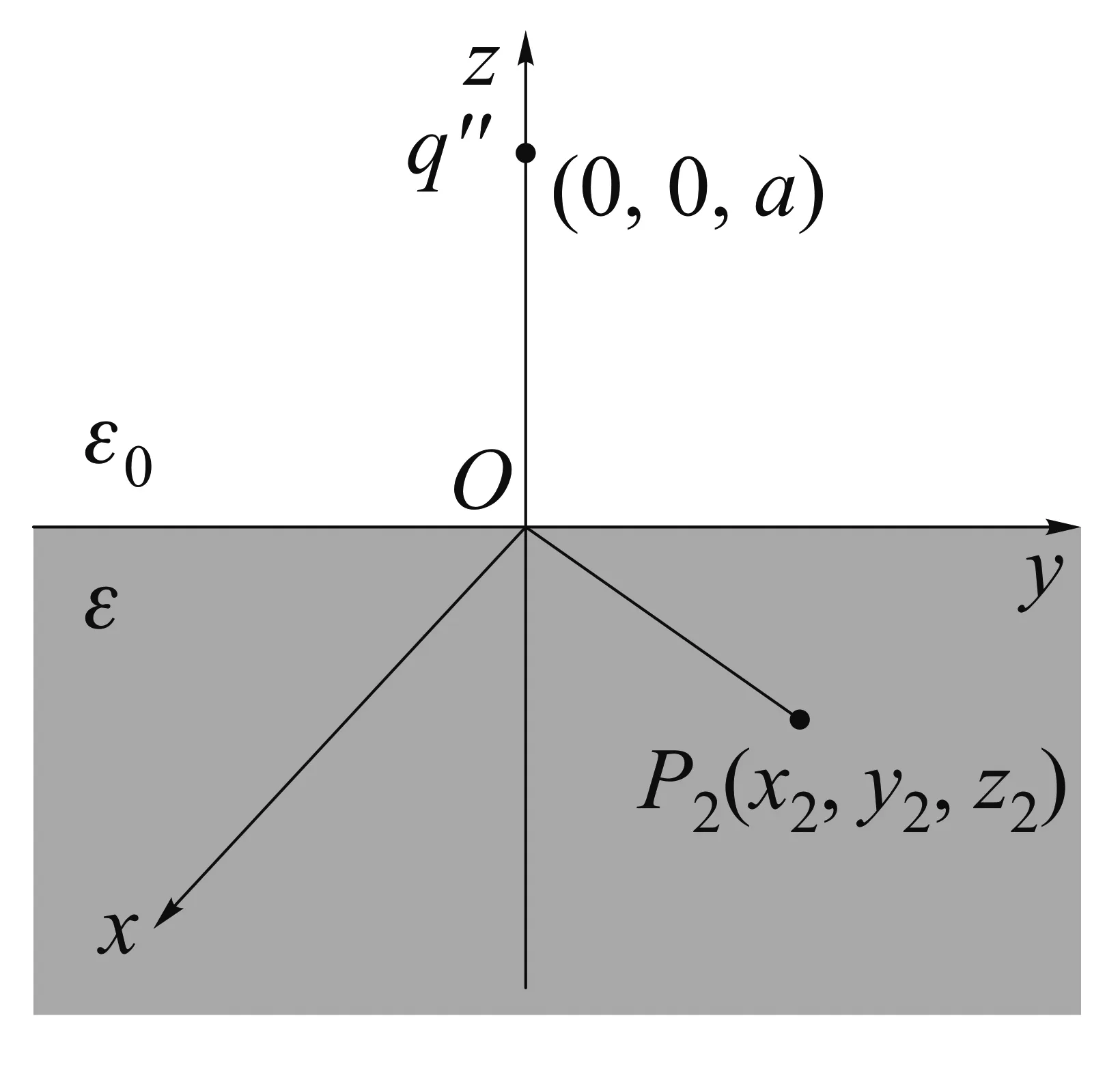
图2 镜像电荷的选择2

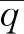
由此可见，在介质存在时，镜像电荷的选择并不唯一，不同的镜像电荷都可以得到相同的场.从数学上讲，这并不难理解，因为在介质存在时，决定镜像电荷的电量的(位置一般由对称性决定了)由两个方程，两个未知数，而不同的方程有不同的解，所以镜像电荷的电量可以不同.而最后的结果与唯一性定理并不矛盾.因为镜像电荷是在保证此空间中的源与边值关系都没有被改变的前提下引入的，那么该空间中的场肯定是唯一的.

不过如果再由电场进一步求出界面的束缚电荷，又会发现，第一种镜像电荷的选择其总电量与整个界面上的总电量相同，但第二种镜像电荷却与之不同.

3 介质交界面上的极化电荷

既然求出了总的电磁场，可根据边值关系求出面上的极化电荷面密度

(10)

对整个无限大平面积分，换到球坐标系

(11)

由此可见，第一种镜像电荷的选择，其总电量与束缚电荷的总电量相同.

但是在上半空间不是真空，而是另外一种介质时，虽然同样可以找到不同的镜像电荷，并得到最终的场(仍然是唯一的).可是这时，由总场算出的束缚电荷的总电荷量并不与任何的一种镜像电荷的电量相同[2].