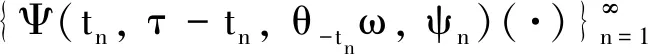非自治随机时滞广义Kuramoto-Sivashinsky方程的拉回随机吸引子
李 勇,张强恒,李扬荣
西南大学 数学与统计学院,重庆 400715
文献[1]研究了广义Kuramoto-Sivashinsky方程的整体吸引子及其性质,文献[2]对随机广义Kuramoto-Sivashinsky方程的随机吸引子进行了研究.本文主要研究在一维有界区域O=[-L,L]上的时滞广义Kuramoto-Sivashinsky方程
(1)
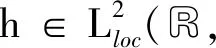
(E1)g(0)=0,g′(l)≤b;
(E2) |f(l)|≤A1|l|p,|f′(l)|≤A2|l|p-1;
(E3)φ′(l)≤m,|φ′(l)|≤B1|l|q,|φ″(l)|≤B2|l|q-1;
其中A1,A2,B1,B2,m,CF和LF是正实数,b是负实数,而且2≤p<7,1 拉回随机吸引子最初是由文献[3]提出来的,文献[4-5]对非自治随机动力系统的拉回随机吸引子问题进行了讨论,文献[6-7]对时滞微分方程的拉回随机吸引子的问题进行了一系列的讨论.本文主要研究在状态空间Xρ=C([-ρ,0],L2(O))上的拉回随机吸引子的存在性. 在空间(Ω,F,P)上定义一簇遍历的保测变换{θt}t∈R: θtω(·)=ω(·+t)-ω(t) ∀ω∈Ω,t∈R (2) (3) (4) Ψ(t,τ,ω,ψ)(·)=vt+τ(·,τ,θ-τω,ψ) (5) (6) 其中λ为庞加莱不等式常数.定义映射 (7) (8) (9) 引理1假设(E1),(E2),(E3),(E4),(5)式和(6)式成立,则对任意的τ∈R,ω∈Ω和D∈D,存在T=T(τ,ω,D)≥4ρ+1,使得对任意t≥T,σ∈[τ-3ρ-1,τ],ψ∈D(τ-t,θ-tω),v满足 ‖vσ(·,τ-t,θ-τω,ψ)‖2≤R(τ,ω) 其中R(τ,ω)定义为 (10) C为依赖于τ,ω和D的正实数. 证用方程(4)与v做内积,得 (11) 由(E1),(E2),(E3),(E4),对任意ε>0有 (12) (13) (14) (15) (16) 由(5)式和(11)-(16)式可得 (17) (18) (19) 用τ-t和θ-τω分别代替τ和ω,则σ≥τ-t+ρ,令σ∈[τ-3ρ-1,τ],则t≥4ρ+1,可以得到 (20) (21) 由(2)式和(8)式,对任意ε>0和ω∈Ω,存在T(ε,ω)≥4ρ+1,使得对任意|t|≥T(ε,ω)都有 (22) (23) (24) 则由(20)-(24)式可得,存在T≥4ρ+1,当t≥T时引理1成立. 引理2[1]V是周期为2L的光滑周期函数,成立以下不等式: 引理3假设(E1),(E2),(E3),(E4),(5)式和(6)式成立,则对任意的τ∈R,ω∈Ω和D∈D,存在T=T(τ,ω,D)≥4ρ+1,使得对任意t≥T,σ1∈[τ-ρ-1,τ],ψ∈D(τ-t,θ-tω),v满足 其中R1(τ,ω)为依赖于τ,ω和D的正实数. 证用方程(4)与-vxx做内积,得 (25) 由假设(E1),(E2),(E3),(E4)以及引理2和Young不等式,得 (26) (27) (28) (29) (30) (31) (32) 则由(25)-(32)式可以得出 (33) 由引理1可得 (34) (35) 令τ∈R,t≥4ρ+1,ω∈Ω,κ∈(τ+s-2ρ-1,τ+s-ρ-1),s∈[-ρ,0],σ1∈[τ-ρ-1,τ],对(33)式在[κ,σ1+s]上求积分,用τ-t和θ-τω分别代替τ和ω,则由(34),(35)式可以得出 (36) 与(36)式的证明类似,对(33)式在[τ-ρ,τ]上积分,由(34),(35)和(36)式可得 (37) 其中Q1(τ,ω),Q2(τ,ω)为依赖于τ,ω和D的正实数.由(5),(36)和(37)式得引理3成立. 引理4假设(E1),(E2),(E3),(E4),(5)和(6)式成立,则对任意τ∈R,ω∈Ω和D∈D,存在T=T(τ,ω,D)≥4ρ+1,使得对任意t≥T,ψ∈D(τ-t,θ-tω),v满足 其中R2(τ,ω)是依赖于τ,ω和D的正实数. 证用方程(4)与vxxxx做内积,可得 (38) 由假设(E1),(E2),(E3),(E4)以及引理2,可得 (39) (40) (41) (42) (43) 由(38)-(43)式可以得出 (44) 由引理2可得 (45) 令τ∈R,t≥4ρ+1,ω∈Ω,κ1∈(τ+s-1,τ+s),s∈[-ρ,0],κ1≤κ2,对(44)式在[κ1,κ2+s]上求积分,用τ-t和θ-τω分别代替τ和ω,再用τ代替κ2,由(34),(35),(45)式可得 (46) 与(46)式的证明类似,对(44)式在[τ-ρ,τ]上积分,由(34),(35),(45),(46)式可得 (47) 引理5假设(E1),(E2),(E3),(E4),(5)式和(6)式成立,则非自治随机动力系统Ψ有一个闭的可测的D-拉回吸收集K={K(τ,ω):τ∈R,ω∈Ω}∈D,K(τ,ω)定义为 其中R(τ,ω)由(10)式定义. 证由引理1,对任意的τ∈R,ω∈Ω和D∈D,存在T=T(τ,ω,D)>0,使得对任意t≥T有 Ψ(t,τ-t,θ-tω,D(τ-t,θ-tω))⊆K(τ,ω) 引理6假设(E1),(E2),(E3),(E4),(5)式和(6)式成立,则非自治随机动力系统Ψ在Xρ上是D-拉回预紧的. 为了证明在Xρ上vτ(·,τ-tn,θ-τω,ψn)是预紧的,首先证明vτ(·,τ-tn,θ-τω,ψn)在Xρ上等度连续,由假设(E1),(E2),(E3),(E4)以及引理1、引理3、引理4和(4)式可知,存在N1=N1(τ,ω)>0,使得对任意n>N1有 其中c=c(τ,ω)>0.因此对任意n>N1,s1,s2∈[-ρ,0],且s1>s2,有 定理1假设(E1),(E2),(E3),(E4),(5)式和(6)式成立,则连续非自治随机动力系统Ψ在Xρ上存在D-拉回随机吸引子. 证由于引理5和引理6的结论满足文献[3]中D-拉回随机吸引子的存在性条件,所以连续非自治随机动力系统Ψ在Xρ上存在D-拉回随机吸引子.1 连续非自治随机动力系统

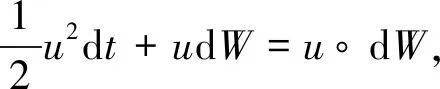


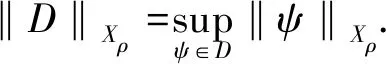


2 解的一致估计
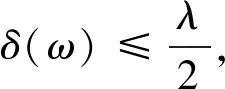
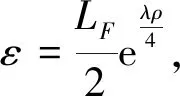
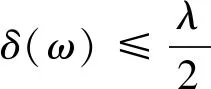

3 拉回吸引子