关于不定方程x2+4n=y11的整数解*

蔡 小 群

(华南师范大学 数学科学学院，广州 510631)

0 引 言

设B∈N, 研究Lebesgue-Nagell不定方程:

x2+B=yk

(1)

的整数解是数论中不可或缺的一部分。

最初，Lebesgue[1]证明了当B=1时，式(1)仅有整数解(x,y)=(0,1)；潘承洞等[2]证明了当B=1，k=3时,式(1)仅有解(x,y)=(0,1)；当B=4，k=3 时,式(1)仅有解(x,y)=(±2,2)，(±11,5)。近年来, 不少学者研究了B=4n，n≥1 时，式(1)的整数解[3-28]。文献[19]提出以下猜想:

文献[9]与[19] 分别证明了k=5,9时猜想1成立。本文将验证k=11时，猜想1也成立。为此，首先证明不定方程x2+4n=y11在x为奇数，n≥1时无整数解, 再证明不定方程x2+4n=y11在n∈{1,8,9,10} 时均无整数解, 进而证明k=11时猜想1成立，即证明不定方程x2+4n=y11有整数解的充要条件是n≡0(mod 11)或n≡5(mod 11)，且当n≡0(mod 11)时，其整数解为(x,y)=(0,4m)；当n≡5(mod 11)时，其整数解为 (x,y)=(±211m+5,22m+1)，这里的m为非负整数。

1 相关概念、性质及记号

定义2[2]设M=(M,⊕,⊗)是一个整环，α,β∈M， 若存在单位元素ε，使β=ε⊗α，则称β是α的相伴数, 记作β～α。

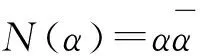
性质1[2]设α,β∈Z[i]，若α|β，则N(α)|N(β)。

以下， 为方便起见，把α⊗β记为αβ。

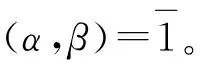
α=ε1μk，β=ε2νk

这里ε1,ε2是M中的单位元素, 且ε1ε2=εk，ε为单位元素。

引理2[19]在Z[i]中, 若δ|2, 则在相伴意义下,δ∈{1,1+i,2}。

引理3[1]不定方程x2+40=y11仅有整数解(x,y)=(0,1)。

引理4[20]不定方程x2+42=y11无整数解。

引理5[21]不定方程x2+43=y11与x2+44=y11均无整数解, 且不定方程x2+45=y11仅有整数解(x,y)=(±32,2)。

引理6[21]不定方程x2+46=y11与x2+47=y11均无整数解。

2 主要结论及证明

本节首先证明当x为奇数，n≥1 时, 不定方程x2+4n=y11无整数解，再证明不定方程x2+4n=y11(n∈{1,8,9,10})无整数解，最后给出不定方程x2+4n=y11有整数解的充要条件。

引理7 不定方程x2+4n=y11当n≥1，x为奇数时无整数解。

证明不定方程x2+4n=y11在Z[i]中可表示成(x+2ni)(x-2ni)=y11。

设δ=(x+2ni,x-2ni), 由x是奇数知(2x,2n+1i)=2，从而δ|2。由引理2知，δ可取1,1+i,2。以下将分3种情形进行证明。

情形1 若δ=2， 由x为奇数知x+2ni为奇数，与δ|(x+2ni)矛盾, 故δ≠2。

情形2 若δ=1+i, 由性质1知N(1+i)|N(x+2ni), 即2|(x2+4n), 这与x为奇数矛盾, 故δ≠1+i。

情形3 若δ=1，由引理1及Z[i]中的任一单位元素均可表为其中一个单位元素的11次方可设x+2ni=(a+bi)11, 这里a,b∈Z。从而有

x=a11-55a9b2+330a7b4-462a5b6+165a3b8-11ab10

(2)

2n=b(11a10-165a8b2+462a6b4-330a4b6+55a2b8-b10)

(3)

因为a,b∈Z, 由式(3)可得b=±2t(0≤t≤n)。下面将分t=0，1≤t≤n-1(n≥2)，t=n这3种情形进行讨论。

情形1t=0。

此时将b=±1代入式(2)，得

x=a11-55a9+330a7-462a5+165a3-11a≡

a11-55a9+165a3-11a(mod 2)

易见x为偶数，这与x为奇数矛盾。

情形2 1≤t≤n-1，这里n≥2。

将b=±2t(1≤t≤n-1)代入式(3)，得

±2n-t=11a10-165a8b2+462a6b4-330a4b6+55a2b8-b10

显见a是偶数，从而由式(2)知x为偶数，这与x为奇数 矛盾。

情形3t=n。

子情形3.1b=2n。

将b=2n代入式(3)，得

11a2(a8-15a6b2+42a4b4-30a2b6+5b8)=
210n+1

(4)

对式(4)两边同时取模11, 式(4)左边≡0(mod 11), 而右边≡2(mod 11)， 显然矛盾。

子情形3.2b=-2n。

子情形3.2.1n=1。

此时将b=-2 代入式(3)，得

11a2(a8-15a6b2+42a4b4-30a2b6+5b8)=3×11×31

由a∈Z易得a2=1。

将a2=1,b=-2 代入式(3)整理得-27=93， 矛盾。

子情形3.2.2n≥2。

将b=-2n代入式(3)得

11a10-165a8b2+462a6b4-330a4b6+55a2b8=
210n-1

(5)

由式(2)及x为奇数可知a为奇数, 从而a2≡1(mod 8)。对式(5)两边同时模8,由n≥2可知式(5)左边≡11a10≡3(mod 8)，而右边≡7(mod 8)，矛盾。

综上所述，不定方程x2+4n=y11当x为奇数时无整数解。

引理8 不定方程x2+4=y11无整数解。

证明分x的奇偶性进行分类讨论。

情形1x为奇数。

由引理7可知不定方程x2+4=y11无整数解。

情形2x为偶数。

综上可知，不定方程x2+4=y11无整数解。

引理9 不定方程x2+4n=y11(n=8,9,10)无整数解。

证明分x为奇数和偶数两种情况分别证明。

情形1x为奇数。

由引理7可知此时,不定方程x2+4n=y11(n=8,9,10)无整数解。

情形2x为偶数。

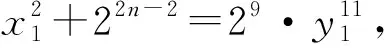
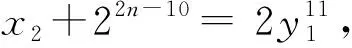
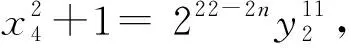
综上可知, 不定方程x2+4n=y11(n=8,9,10)无整数解。

定理1 不定方程x2+4n=y11有整数解的充要条件是n≡0(mod 11)或n≡5(mod 11)，且当n≡0(mod 11)时,其整数解为(x,y)=(0,4m)；当n≡5(mod 11)时,其整数解为 (x,y)=(±211m+5,22m+1)，这里的m为非负整数。

证明充分性显然, 仅证必要性, 即证当不定方程x2+4n=y11有整数解时的充要条件是n≡0(mod 11)或n≡5(mod 11)，且当n≡0(mod 11)时,其整数解为(x,y)=(0,4m)；当n≡5(mod 11)时,其整数解为 (x,y)=(±211m+5,22m+1)，这里的m为非负整数。

以下按x的奇偶性进行分类证明。

情形1x为奇数。

此时由引理 3 及引理7知, 不定方程x2+4n=y11无整数解。

情形2x为偶数。

不失一般性, 不妨设n=11m+l, 其中l∈{0,1,…,10}, 这里m是非负整数。下面对m用数学归纳法进行证明。

当m=0 时, 由引理3—6，引理8及引理9知结论成立。

当m=1时,x2+4n=y11可表示成x2+411+l=y11。

由m=0的结论可知，不定方程u2+4l=v11有整数解时l=0或l=5，且当l=0 时，其整数解为(u,v)=(0,1)；当l=5时，其整数解为(u,v)=(±25,2)。因此不定方程x2+411+l=y11有整数解时，11+l≡0(mod 11)或11+l≡0(mod 11)，且当l=0时，其整数解为(x,y)=(0,41)；当l=5时, 其整数解为(x,y)=(±211×1+5,22×1+1)。故m=1时结论成立。

假设m=t(t>1)时结论成立,即当x2+411t+l=y11有整数解时，11t+l≡0(mod 11)或11t+l≡0(mod 11),且当l=0时，其整数解为(x,y)=(0,4t)；当l=5时，其整数解为(x,y)=(±211t+5,22t+1)。下证当m=t+1时, 即n=11(t+1)+l时, 结论也成立。

此时不定方程x2+4n=y11可表示成x2+411(t+1)+l=y11，即x2+411+(11t+l)=y11。类似于m=1的证明过程可知,x2+411+(11t+l)=y11有整数解当且仅当u2+411t+l=v11有整数解, 且有解时，有x=211u,y=4v。由归纳假设可知，u2+411t+l=v11有整数解时，11t+l≡0(mod 11)或11t+l≡5(mod 11)，且当l=0时, 其整数解为(u,v)=(0,4t)；当l=5时,其整数解为(u,v)=(±211t+5,22t+1)。故当x2+411(t+1)+l=y11有整数解时，11(t+1)+l≡0(mod 11)或11(t+1)+l≡5(mod 11),且当l=0时,其整数解为(x,y)=(0,4t+1)；当l=5时其整数解(x,y)=(±211(t+1)+5,22(t+1)+1)。从而当m=t+1时,结论也成立。

综上，由数学归纳法可知结论成立。证毕。

显见，由定理1及已知结果，可知猜想1在k=5,9,11时已成立。在后续研究中，将证明k=7时猜想1也成立。