局部修复码综述

邢朝平

（上海交通大学 电子信息与电气工程学院，上海200030）

随着计算机技术和网络技术的发展，数据正以爆炸式的速度增长，对存储系统提出了巨大的挑战.分布式存储系统因其海量存储能力、高扩展性和低成本等特性受到广泛开发和使用.面临海量数据存储的大背景，当前大型分布式存储系统的存储规模越来越大，存储设备的质量往往得不到保障，导致存储系统中的节点出现故障.如何有效保障数据可靠性也成为当前分布式存储系统重点关注的问题之一.为了保障数据的可靠性，传统的方法是使用备份的方法.但是随着数据爆炸式增长，存储成本越来越为大型分布式存储系统所关注.备份的方法需要占用大量的存储空间.相较于备份这种容错技术，基于纠删码的容错存储技术能够在保证一定的可靠性的前提下，降低冗余存储开销，因而在实际存储系统中被广泛的部署.国际上很多数据存储的大公司，例如谷歌、微软、Dropbox、Windows Azure、HDFS、Amazon等已经相继采用纠删码技术来保证存储系统中数据的可靠性.纠删码起源于通信传输领域，原先主要是用于解决数据传输中的纠错问题，后来逐渐应用到存储系统中的数据检错和纠错问题中，以提高存储系统的可靠性.目前，根据存储系统应用的特点和需求，人们对纠删码进行了一系列的推广并且针对具体的存储模型提出了各种各样的解决方案.

良好的容错技术通常要求存储系统具有低的冗余开销、低修复带宽以及高的错误容忍度.如何在这三者之间达到最优的权衡是该领域的关键研究方向.传统的纠删码的思想是当出现错误的时候，利用码的全局纠错能力把整个码字都恢复出来.然而已有统计数据表明在存储系统中，很大的可能都是一个节点或者少数几个节点失效，因而大多数研究主要针对如何以较低的修复带宽来修复一个或两个失效的节点.为了降低修复带宽，人们提出了局部修复码的概念，即通过访问少数可用节点就可恢复失效的节点，从而达到比较少的计算量及带宽.如今局部修复码在分布式存储中已被广泛应用，尤其是在大数据的可靠性及云存储方面起着重要作用.

本文介绍国际上目前比较热门的三类局部修复码，即经典的局部修复码、再生码和极大局部修复码.重点是介绍这三类码的最优性质.第一节介绍基本概念及必要的基础知识.第二节综述最优局部修复码及构造.第三节综述达到cut-set界的再生码及构造.最后一节综述最优极大局部修复码及构造.

1 基本概念

本节将介绍一些基本概念及必要的基础知识，包括线性码、广义Reed-Solomon码以及局部译码等相关结论.这些基础知识为后面的研究提供了理论依据.下面首先介绍码的一些相关结论，读者可参考文献［1-2］.设q为一个素数幂，Fq表示含有q个元素的有限域表示Fq上的n维向量空间，即

1.1 码的相关结论的每个非空子集C称为一个码长为n的q元码，C中向量叫做码字，｜C｜称为码字个数，k＝logq｜C｜称为信息位数.若码长为n的q元码C的码字个数｜C｜＝M，则称C为（n，M）q码.若恰为Fq-线性子空间，则称C为q元线性码.此时码的信息位数k恰为子空间C的维数.码长为n，信息位数为k的q元线性码可以表示成［n，k］q.以线性码C的一组基为行向量构成的矩阵G称为C的生成矩阵，以G的解空间的一组基为行向量构成的矩阵H称为C的校验矩阵.记

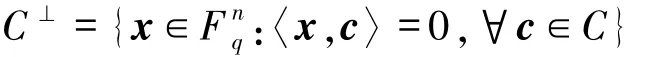
为C的对偶码.

除了码长和码字个数（或信息位数）之外，码还有一个非常重要的参数——最小距离.在介绍最小距离之前，先简单回顾一下Hamming距离.设向量

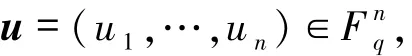
记［n］＝｛1，2，…，n｝，向量u的支撑集定义为

向量u的汉明重量wtH（u）定义为

两个向量u、v的Hamming距离dH（u，v）定义为

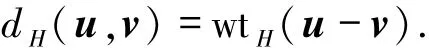
由此可以给出码的最小距离的定义（在本文余下部分，若无混淆的话将省略下标H）.

定义1.1设是一个q元码.C的最小距离d（C）定义为

特别地，线性码C的最小距离为

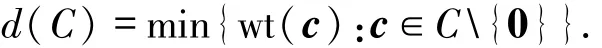
码长为n，信息位数为k，最小距离为d的q元线性码可以表示成［n，k，d］q.码的各个参数之间彼此制约，比如常用的Singleton界.

引理1.1［2］（Singleton界）q元［n，k，d］线性码C的参数满足

若q元［n，k，d］线性码C的参数满足n+1＝k+d，则称码C为极大距离可分码，简称为MDS码.

为了更好地描述MDS码，接下来引入信息集的概念.

定义1.2设C为q元（n，qk）码.若I⊆［n］满足｜I｜＝k且

其中cI是c在I上的投影，则称I为C的一个信息集.

MDS码是一类非常重要的码，纠错能力强，在局部修复码中有着非常广泛的应用.下面给出MDS码的信息集的性质.

引理1.2q元（n，qk）码C是MDS码当且仅当每个元素个数为k的子集I⊆［n］都是C的一个信息集.

证明一方面，设（n，qk）q码C是MDS码，I⊆［n］是任一元素个数为k的集合.考虑映射

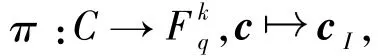
由C为MDS码可知映射π是单射，所以

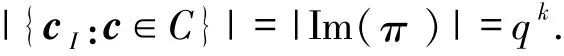
由定义可知，I⊆［n］是C的一个信息集.

另一方面，设集合［n］的每个元素个数为k的子集I都是C的一个信息集.反证，假设C不是MDS码，则有d≤n-k.从而存在两个码字u，v∈C使得d（u，v）＝d，即

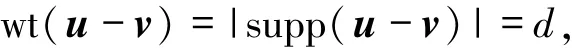
所以

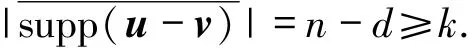
不妨设I是的一个子集，且｜I｜＝k，则I是C的一个信息集.根据定义有

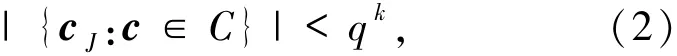
（1）与（2）式矛盾，假设不成立，因此C是MDS码.

下面的引理总结了MDS码的若干等价刻画.

引理1.3［3］设［n，k］q线性码C的生成矩阵和校验矩阵分别是G和H，则下面的结论是等价的：

1）C是MDS码；

2）H的任意n-k列线性无关；

3）G的任意k列线性无关；

4）C⊥是MDS码；

5）任意一个元素个数为k的集合I⊆［n］都是C的一个信息集；

6）任意一个元素个数为n-k的集合I⊆［n］都是C⊥的一个信息集.

回顾一类最常见的MDS码——广义Reed-Solomon码.设α1，α2，…，αn是有限域Fq中n个不同的元素（从而n≤q），v1，v2，…，vn均为Fq中的非零元素，整数k满足1＜k＜n.记a＝（α1，α2，…，αn）和v＝（v1，v2，…，vn）.

定义1.3广义Reed-Solomon码被定义为GRSk（a，v）＝｛（v1f（α1），v2f（α2），…，vnf（αn））：

f（x）∈Fq［x］；degf（x）＜k｝.

引理1.4［1］GRSk（a，v）是［n，k，n-k+1］q线性码，因此GRSk（a，v）是MDS码.

引理1.5［2］GRSk（a，v）的对偶码也是广义Reed-Solomon码，并且有

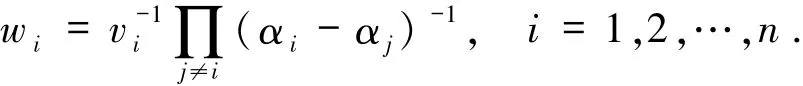
1.2 MRD码和对偶基通过向量空间的Fq-同构，可以把Fq N中的元素看做是中的列向量.因此，向量对应一个Fq上的N×n矩阵U（不妨设n≤N）.

定义1.4两个向量之间的秩距离dR（u1，u2）定义为rank（U1-U2），其中U1，U2∈FqN×n分别对应u1，u2.的每一个子集C称为一个秩度量码.秩度量码C的最小秩距离dR（C）定义为

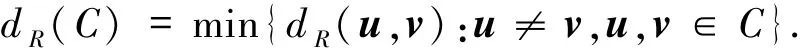
若C是的一个Fq N-子空间，则称C为线性秩度量码.类似于经典码的Singleton界，秩度量码的参数满足如下结论.

引理1.6［4］（秩度量码的Singleton界） 维数为k，最小秩距离为d的Fq N-线性秩度量码C⊆的参数满足

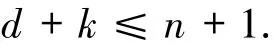
达到Singleton界的秩度量码被称为最大秩距离码（简称为MRD码）.文献［4］给出了MRD码的判别准则.

引理1.7［4］设是维数为k的Fq N-线性秩度量码，其生成矩阵为则C是MRD码当且仅当对于每个中任意秩为k的矩阵M，矩阵GMT是可逆的.

下面介绍有限域上的对偶基.

定义1.5设Fq／Fp是有限域扩张，且

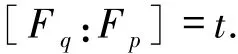
设｛ζ1，ζ2，…，ζt｝是Fq的一组Fp-基，若Fq上另一组Fp-基｛θ1，θ2，…，θt｝满足

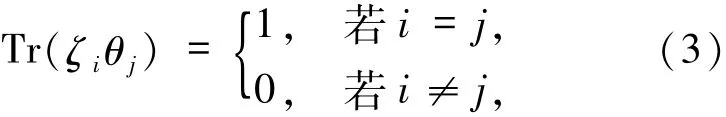
其中Tr是Fq到Fp的迹映射，则称｛θ1，θ2，…，θt｝为｛ζ1，ζ2，…，ζt｝的对偶基.

已知对于Fq的任意一组Fp-基，其对偶基总是存在的［5］.可以利用对偶基和迹映射将扩域上元素表示出来.若固定Fq的一组Fp-基｛ζ1，ζ2，…，ζt｝及其对偶基｛θ1，θ2，…，θt｝，对于任意的α∈Fq，不妨设其中ai∈Fp，则对于任意的j∈［n］，由对偶基定义可知

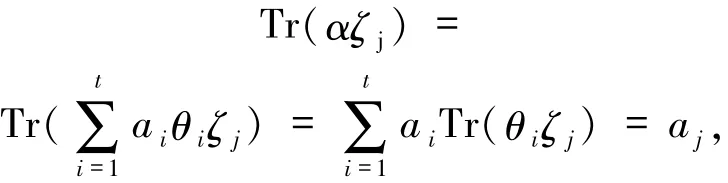
因此α可表示为

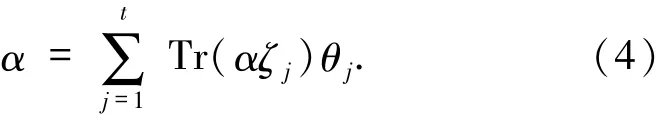
1.3 纠删码和局部译码在分布式网络存储系统中需要考虑的是如何修复某个（些）故障的节点.这种类型的错误称为删除错误，即错误的位置是已知的.本文研究的是在网络存储中对删除错误使用局部译码来恢复网络中的某个故障节点，即用网络中的部分而不是全部节点去修复.对存储系统中使用的删除编码通常要满足以下要求：1）局部性低，用尽可能少的节点去修复；2）带宽低，修复需下载的数据量尽可能小；3）节点计算少；4）硬件实现容易；5）有高效的译码算法等.

事实上，码的最小距离和可纠正删除错误个数之间有密切的关系.

引理1.8q元（n，M）码C可纠正d-1个删除错误当且仅当d（C）≥d.

证明（n，M）q码C可纠正d-1个删除错误等价于：对于任意的元素个数为d-1的集合I⊆［n］以及任意的u，v∈C，u＝v当且仅当u¯I＝v¯I，其中¯I＝［n］＼I.

一方面，设d（C）≥d.若对于任意的元素个数为d-1的集合I⊆［n］以及任意的u，v∈C有u¯I＝v¯I，则有d（u，v）≤｜I｜＝d-1，这表明u＝v.

另一方面，设对于任意的元素个数为d-1的集合I⊆［n］以及任意的u，v∈C，u＝v当且仅当u¯I＝v¯I.假设d（C）＜d，则存在两个码字u≠v使得d（u，v）≤d-1.设J是u-v的支撑集，则｜J｜≤d-1.选择I⊂［n］满足｜I｜＝d-1，且J⊂I，则有u¯I＝v¯I，进而u＝v，与u≠v矛盾.

利用上面的引理可以直接得到如下结论.

引理1.9q元（n，M）码C在集合R⊂［n］中可局部纠正d-1个删除错误当且仅当码CR：＝｛cR：c∈C｝的最小距离至少是d-1.

2 最优局部修复码

局部修复码是近几年来一个非常热门的研究方向，主要研究在分布式数据存储系统中通过局部修复提高存储节点修复效率的编码理论和方法.本节将介绍最优局部修复码的相关进展.

2.1 局部修复码及其Singleton-like界

定义2.1设C为码长是n的q元码，若对任意的i∈［n］，存在元素个数为r的子集Ri⊂［n］＼｛i｝使得对于任意的c＝（c1，…，cn）∈C，ci可被｛cj｝j∈R i恢复，则称C为具有局部修复性r的局部修复码，集合Ri称为i的恢复集.

注具有局部修复性r的局部修复码也可有如下的等价刻画：对于任意的i∈［n］，存在元素个数为r的子集Ri⊂［n］＼｛i｝使得对于任意的u，v∈C，有

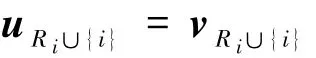
当且仅当uR i＝vR i.也就是说局部修复码中可以通过下载局部r个位置的信息来修复单个删除错误.

下面的引理给出如何从对偶码的角度刻画线性码的恢复集.

引理2.1［6］设C是码长为n的q元线性码.集合R⊂［n］＼｛i｝是i的恢复集当且仅当存在c∈C⊥使得i∈supp（c）⊂R∪｛i｝.

类似于经典码，局部修复码的参数之间也彼此制约，文献［7］中首次给出了局部修复码的Singleton-like界.

引理2.2（Singleton-like界） 若q元［n，k，d］线性码C具有局部修复性r，则有

当r＝k时，上面的Singleton-like界即为经典的Singleton界.若具有局部修复性r的q元［n，k，d］线性码的参数达到Singleton-like界，即

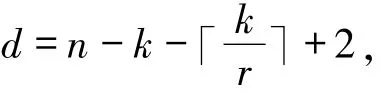
则称C为最优局部修复码.特别地，当（r+1）｜n时，可以给出Singleton-like界的另一种形式，这种形式便于后面通过校验阵刻画最优局部修复码.

引理2.3［6］设整数n、k、d、r满足（r+1）｜n且则

更进一步，还可以得到最优局部修复码的恢复集刚好是［n］的一个划分.

引理2.4［6］设C是参数为［n，k，d］q具有局部修复性r的最优局部修复码.若（r+1）｜n且满足

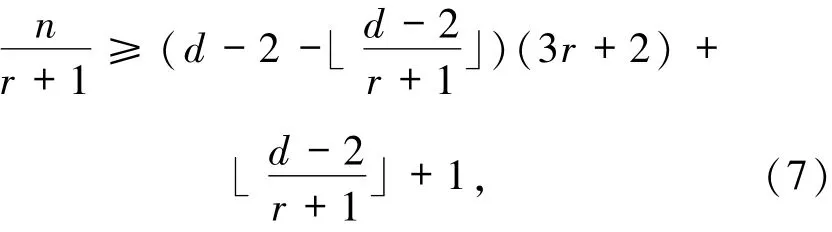
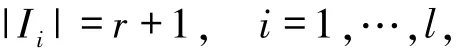
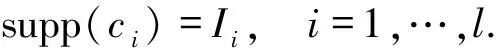
2.2 最优局部修复码码长的两个上界经典的MDS猜想告诉我们，不存在码长超过q+1的非平凡（最小距离d＞2）的q元MDS码，其中当q为偶数且k＝3时，不存在码长超过q+2的q元MDS码.MDS猜想目前只有q为素数的情况被Ball［8］证明.由最优局部修复码和MDS码之间的类比，一个很自然的问题就是当固定字母集大小q后，q元最优局部修复码的最大码长n能否超过q+1.令人惊讶的是，当d＝3，4时，文献［9］中利用循环码构作的最优局部修复码，其码长可以任意大.当d≥5时，最优局部修复码的最大码长和MDS码一样是被q的函数限制的，但可以超过q+1.下面介绍文献［6］中给出的最优局部修复码的两个上界.

定理2.1［6］设C是参数为［n，k，d］q具有局部修复性r的最优局部修复码，设（r+1）｜n且参数满足（7）式，若d≥5且d≡a（mod 4），1≤a≤4，则有

特别地，有n＝O（dq3+4／（d-4））.更进一步，当n＝5，6，分别有n＝O（q2），O（q3）.

对于最小距离d和码长n成比例的情形，利用如下引理同样可以得到码长的一个上界.

引理2.5［10］设C是参数为［n，k，d］q具有局部修复性r的最优局部修复码，则有

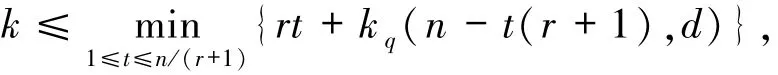
其中kq（m，d）＝max｛k：存在［m，k，d］q线性码｝.

利用上述引理，文献［6］证明了如下结论.

引理2.6［6］设C是q元具有局部修复性r的最优局部修复码，则C的最小距离满足

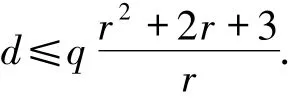
由上述引理直接可以得到当d和n成比例时，最优局部修复码码长的上界.

定理2.2［6］若d＝O（n），且r是常数，则q元具有局部恢复性r的最优局部修复码的码长n满足n＝O（q）.

2.3 利用多项式构造最优局部修复码局部修复码研究中的一个热点问题是如何具体构造出达到Singleton-like界的最优局部恢复码.一个突破性工作是2014年Tamo等［11］利用特殊多项式插值，构造了码长n≤q的q元最优局部修复码.下面介绍一下文献［11］的工作.他们首先刻画了一类在陪集上取值固定的“好的”多项式.

引理2.7［11］记为有限域Fq中非零元构成的集合，则有

1）若H是的乘法子群，则对于任意的β∈多项式在陪集βH上是常值函数，即对于任意的β1，β2∈βH，g（β1）＝g（β2）.

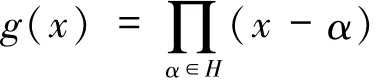
2）若W是Fq的加法子群，则对于任意的β∈Fq，多项式

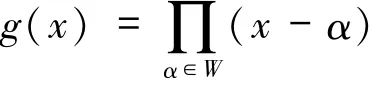
在陪集β+W上是常值函数，即对于任意的β1，β2∈β+W，g（β1）＝g（β2）.

3）设Fl是Fq的子域，W是Fq的Fl-子空间，H是的乘法子群.则对于任意的β∈Fq，多项式

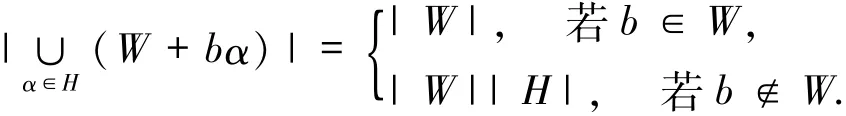
本文仅针对第一种情形介绍文献［11］的构造.设H是的乘法子群，且｜H｜＝r+1.令

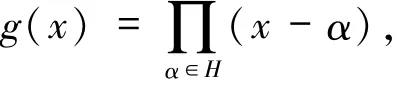
并定义多项式集合

显然，V是Fq-空间且

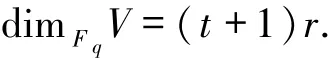
易知C是［m（r+1），（t+1）r，d］q线性码，其中

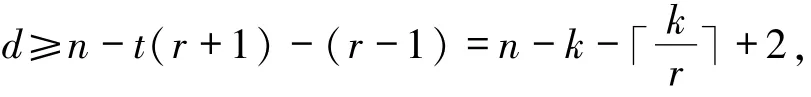
即C的参数达到（5）式.因此要证明C是具有局部修复性r的最优局部修复码只需证明C具有局部修复性r.

设码字（f（β1α1），…，f（β1αr+1），…，f（βmα1），…，f（βmαr+1））∈C，其中f（x）∈V.不失一般性，只需证明f（β1αr+1）能被（f（β1α1），…，f（β1αr））恢复.不妨设

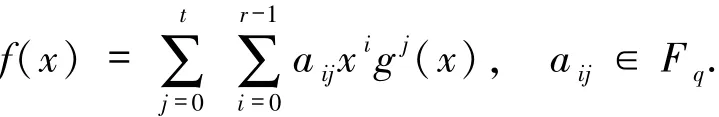
令

则有deg（h（x））≤r-1，且对于1≤m≤r+1，有

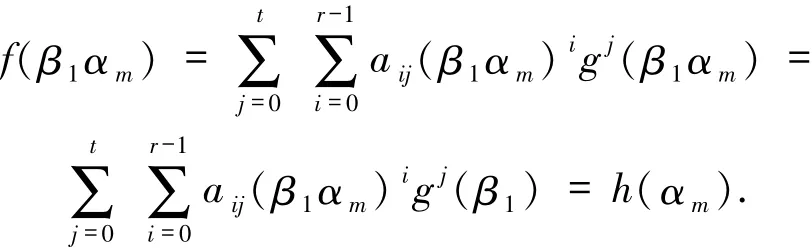
由deg（h（x））≤r-1知，h（x）可完全由h（α1），…，h（αr）决定.因此h（αr+1）可由h（α1），…，h（αr）决定，即f（β1αr+1）能被（f（β1α1），…，f（β1αr））恢复.即表明C具有局部修复性r.利用同样的方法，文献［11］得到了具有如下参数的最优局部修复码.

定理2.3［11］若满足以下条件之一，则存在参数为［n，k，d］q，具有局部修复性r的最优局部修复码.

1）n｜（q-1），（r+1）｜n，存在整数t≥0使得k＝（t+1）r且n＞t（r+1）+r-1.

2）n｜q，（r+1）｜n，存在整数t≥0使得k＝（t+1）r且n＞t（r+1）+r-1.

3）设l是素数幂，存在整数s≥1，使得q＝ls，r+1＝luh，（r+1）｜n，n≤q，其中h｜（l-1），整数u满足1≤u≤d.

类似文献［11］的构造，利用有理函数域的自同构群的结构，文献［12］给出了n≤q+1的最优局部修复码的构造.

定理2.4［12］设（r+1）｜n，若n｜（q-1）或n｜（q+1），则存在码长为n的具有局部修复性r的q元最优局部修复码.

类似文献［11］的构造，利用椭圆函数域的自同构群的结构，文献［13］给出了的最优局部修复码的构造.

定理2.5［13］设当r＝2，3，5，7，11和23时，存在码长为n的具有局部修复性r的q元最优局部修复码.

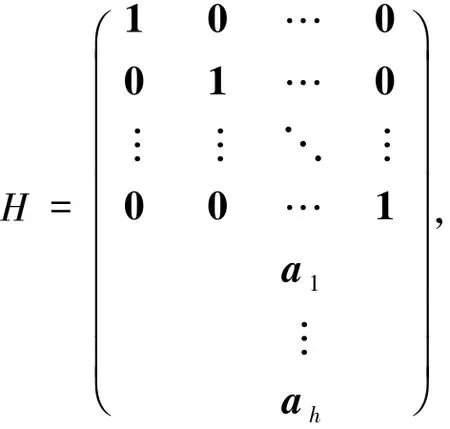
2.4 通过校验阵刻画最优局部修复码由引理2.1、2.3和2.4可知，若（r+1）｜n，则参数为［n，k，d］q具有局部修复性r的最优局部修复码的校验矩阵H有如下形式：且满足H的任意d-1列线性无关，其中1（0）是长为r+1的全1（0）向量，ai是长为n的向量（1≤i≤h），这里本小节将回顾利用校验阵刻画最优局部修复码的部分工作.文献［6］利用校验阵给出了当最小距离d＝2，3，4时，任意码长的最优局部修复码的构造.在此之前，文献［9］利用循环码得到了类似的结论.

定理2.6［6］设d-2≤r，（r+1）｜n.若q≥r+1时，则当最小距离d＝2，3，4时，存在任意码长的最优局部修复码.

证明这里仅证明d＝4的情形.对任意n满足（r+1）｜n，令取

定理2.1证明了当最小距离d≥5时，q元最优局部修复码码长的上界为O（dq3）.文献［6］利用校验阵给出了最优局部修复码的最大码长的一个下界.

定理2.7［6］设d≤r+2，（r+1）｜n，则存在码长为的最优局部修复码.特别地，若r＞3和（r+1）｜n，则存在码长为n＝Ω（q2），最小距离为5的最优局部修复码.

这个证明是非构造性的.特别地，当最小距离d＝5时，由定理2.7知最优局部修复码的最大码长的下界是Ω（q2），而由定理2.1可知此时最大码长的上界同样是O（q2）.也就是说当最小距离d＝5时，最优局部修复码的最大码长的量级为Θ（q2），文献［14］利用常重码的相关结论，通过检验阵刻画给出了一类码长为Θ（q2）的最小距离为5的最优局部修复码的精确刻画.同时文献［14］利用常重码和Moore矩阵还给出了一类偶特征上最小距离为6的最优局部修复码的构造.

定理2.8［14］设r、t为两个正整数，则有

1）若r+1≥5为一个素数幂，则可具体构造出一簇q元具有局部修复性r参数为［n，k，5］的最优局部修复码，其中

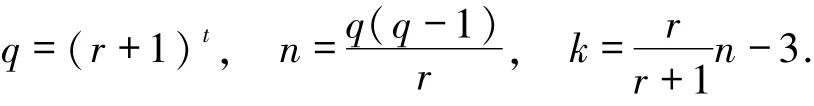
2）设r+1≥8为2的幂次，则可具体构造出一簇q元具有局部修复性r参数为［n，k，6］的最优局部修复码，其中

从定理2.7中可以看出，当d＞6时，存在码长是q1+ϵ量级的最优局部修复码，其中0＜ϵ＜1.很自然的一个问题就是如何精确构造出这样的局部修复码.文献［15］利用校验矩阵构造了q元域上具有局部化参数r＝d-1的参数为［r+1r（q-1），q-r，d］最优局部修复码.

定理2.9［15］设r｜（q-1）且d＝r+1，则存在局部度为r的参数为最优局部修复码.

最后给出两个最优局部修复码中尚未解决的问题：

1）当d≥6时，给出码长为n＝Ω（q1+ε）的最优局部修复码的构造，其中ε＞0为常数.

2）当d＝Ω（n）时，给出码长为n＝Ω（（1+ε）n）的最优局部修复码的构造，或证明其存在性，其中ε＞0为常数.

3 达到cut-set界的再生码

在分布式存储系统中，当某个存储节点失效后，局部修复码采用的方式是通过访问少数可用节点来恢复失效节点.近年来出现的再生码则关注于带宽的消耗.再生码引入网络编码的思想，在修复失效节点时，参与修复过程的节点可进行计算，目的是将最终修复带宽消耗降低.本节将介绍达到cut-set界的再生码的相关研究进展.

3.1 再生码的定义及cut-set界再生码的定义最早由Dimakis等［16］提出.

定义3.1设n、k、d、r、B为正数，若C⊆Fnq满足C＝qk且有：

1）任选码字c＝（c1，…，cn）∈C，对任意的i∈［n］和任意I⊂［n］＼｛i｝满足｜I｜＝r，有ci可被cI恢复；

2）任选码字c＝（c1，…，cn）∈C，对任意的i∈［n］和任意I⊂［n］＼｛i｝满足｜I｜＝d，从｛cj｝j∈I中最多下载B比特可将ci恢复.

则称C是局部度为r，带宽为B的q元（n，k，d）-再生码.

注由定义可以看出局部度为r，带宽为B的q元（n，k，d）-再生码是具有局部性r的q元（n，qk）-局部修复码.不同于局部修复码不需要在每个节点计算，再生码允许在每个节点处计算.

从再生码的思想可以看出，希望使每个结点存储的数据logq和下载带宽B尽可能地小.而每个结点存储的数据量有如下的下界.

引理3.1设C是局部度为r，带宽为B的q元（n，k，d）-再生码.则

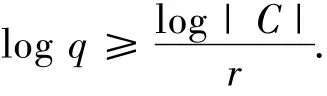
证明因为码字c的每个分量都可被其前r个分量恢复，所以码字c完全被其前r个分量决定，它表明｜C｜≤qr，因此

定义3.2若局部度为r，带宽为B的q元（n，k，d）-再生码C满足即r＝k，则称C为最小存储再生码（简称为MSR码）.

下面的引理说明了MSR和MDS码的等价性.

引理3.2局部度为r，带宽为B的q元（n，k，d）-再生码C是MSR码当且仅当C是MDS码.

证明一方面，设C是局部度为r＝k，带宽为B的q元（n，k，d）-再生码，则每个码字都可被任意k个分量恢复，这表明任意元素个数为k的集合I⊂［n］都是一个信息集，由引理1.3可知C是MDS码.另一方面，设C是MDS码.由引理1.3可知任意元素个数为k的集合I⊂［n］都是一个信息集，因此码字的每个分量都可被其它任意的k个分量恢复，即局部度为r＝k.因此C是MSR码.

由于局部度为r，带宽为B的q元（n，k，d）-MSR码满足r＝k，因此接下来就直接说带宽为B的q元（n，k，d）-MSR码.针对MSR码，希望带宽B尽可能地小.文献［16］给出了带宽B的cut-set下界.

引理3.3［16］（cut-set界） 设C是带宽为B的q元（n，k，d）-MSR码，则

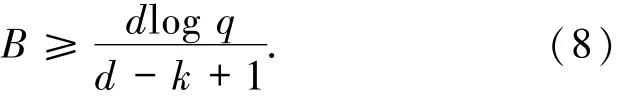
当logq相对于n-k充分大时，（8）式的等号可以达到.而当logq相对于n-k比较小时，（8）式的等式无法达到.常用更平凡的界替代它：

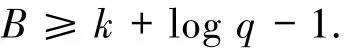
特别当d＝n-1时，（8）式化为

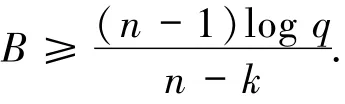
引理3.4［16］设C是q元（n，qk）MDS码，对于每个码字c＝（c1，…，cn）∈C，对任意i∈［n］，从任意di个位置中下载Bi比特可将ci恢复，则有

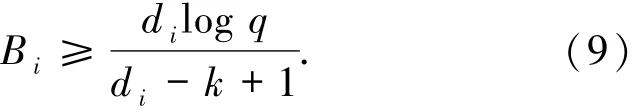
研究达到cut-set界的MSR码是再生码研究中所关心的问题.如文献［17］研究了码率≤1／2的情形，文献［18-20］研究了码率＞1／2的情形.

3.2 Reed-Solomon码可达到cut-set界Reed-Solomon码在编码学中有着非常广泛的应用.再生码概念提出后的一段时间里，人们普遍认为Reed-Solomon码可能不是很好的再生码.而Guruswami等［21］给出了Reed-Solomon码的一个线性的修复算法，证明了在某些参数的情况下Reed-Solomon码可达到cut-set界.在文献［21］工作的基础上，Tamo等［22］利用Reed-Solomon码具体构造出达到cutset界的再生码.本小节介绍他们的工作.

3.2.1Reed-Solomon码的修复算法 首先介绍Guruswami等［21］的工作.设q＝pt，ζ1，…，ζt是Fq的一组Fp-基，θ1，…，θt为其对偶基.设GRSk（a，1）为定义1.3中给出的q元Reed-Solomon码.

定理3.1［21］设正整数k、l、d满足k+l≤d，给定i∈［n］，若对于每个u∈［t］，总存在次数不超过l的多项式hu（x）使得hu（αi）＝ζu，则对任意i∈［n］，GRSk（a，1）中第i个分量可通过下载

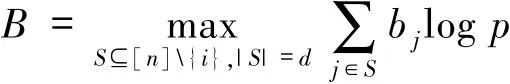
比特来修复，其中

bj＝dimF pSpanF p｛hu（αj）：u＝1，2，…，t｝.（10）

证明为了文章的可读性，这里简单介绍下文献［21］的证明.设GRSn-k（a，w）是GRSk（a，1）的对偶码，其中

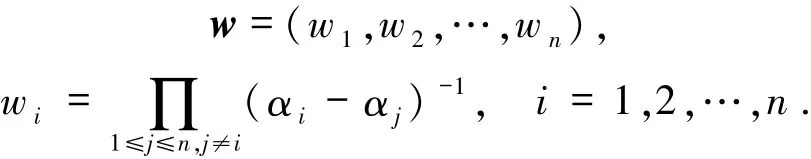
设（f（α1），f（α2），…，f（αn））∈GRSk（a，1），其中degf（x）≤k-1.假设要恢复f（αi）.设S⊆［n］＼｛i｝且｜S｜＝d.令

则有degg（x）＝n-d-1≤n-（l+k）-1，g（αi）≠0且g（αm）＝0，m∈［n］＼（S∪｛i｝）.对于j∈S，考虑空间

Hj＝SpanF p｛hu（αj）：u＝1，2，…，t｝.

设Jj⊆［t］且｜Jj｜＝bj使得｛hs（αj）：s∈Jj｝是Hj的一组Fp-基.从存储f（αj）的节点下载

由Hj的定义可知，对于任意的u满足1≤u≤t，存在Fp中一组数｛λs｝s∈J j使得

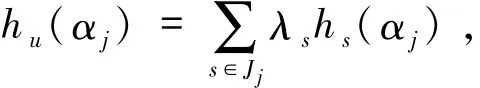
从而有

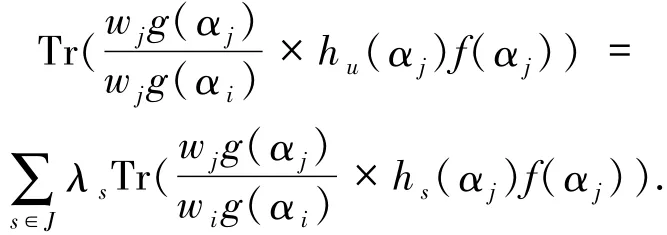
上式表明，从已下载的数据可以计算出

其中1≤u≤t，j∈S.

由对偶基的定义可知

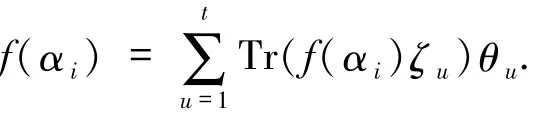
由

和

可得

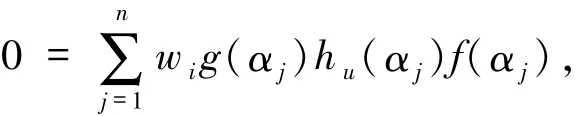
即

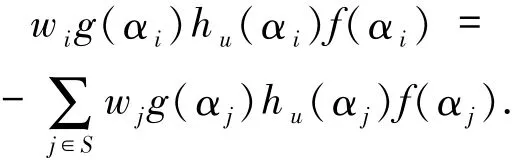
因此

结论得证.

3.2.2达到cut-set界的Reed-Solomon码的构造 现在介绍Tamo等［22］构造的达到cut-set界的再生码.首先介绍部分节点达到cut-set界的结论.

设正整数n、k满足n＞k，取m＝π（n-k），其中π（n-k）表示小于或等于n-k的素数的个数.设素数幂p满足p≥n-m，l1，…，lm是不超过n-k的素数全体.选取m个不同的元素α1，…，αm∈¯Fp使得

令

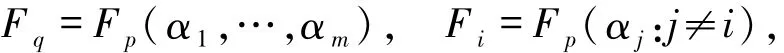
则有

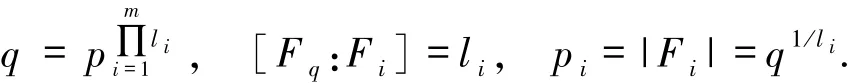
从Fp中选择n-m个不同的元素αm+1，…，αn.令

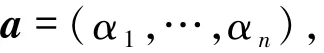
可得q元Reed-solomon码GRSk（a，1）.

定理3.2［22］Reed-Solomon码GRSk（a，1）的前m个节点达到（9）式的cut-set界.

证明简略叙述下证明过程.只需证明，对于1≤i≤m，从任意的di＝li+k-1个点下载比特即可修复第i个分量.

考虑域扩张Fq／Fi，可知是Fq的一组Fi-基.令，则有由定理3.1可知，只需下载

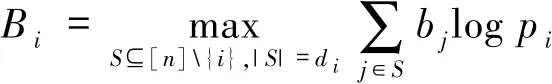
比特即可恢复第i个分量，其中

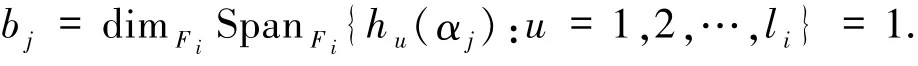
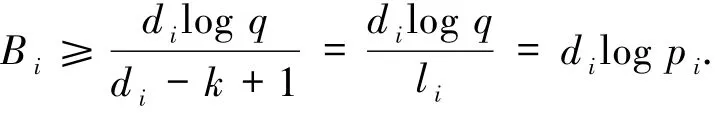
故结论得证.

利用类似的方法，Tamo等［22］构造了全部节点都达到cut-set界的再生码.设正整数n、d、k满足n＞d＞k，设p是一个素数，取s＝d-k+1.由Dirichlet定理可知，存在无穷多个素数l满足l≡1（mods）.选取n个不同素数l1，l2，…，ln，使得li≡1（mods）.选取αi∈¯Fp使得［Fp（αi）：Fp］＝li.定义

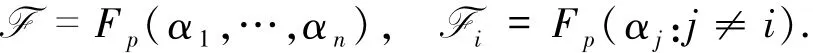
设Fq是F的s次扩域，则有

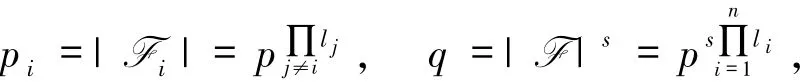
并且有

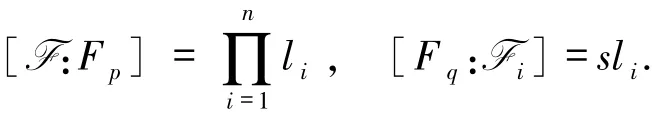
令a＝（α1，…，αn），考虑q元Reed-Solomon码GRSk（a，1）.

定理3.3［22］上述GRSk（a，1）是带宽为B的q元（n，k，d）-MSR码，其中从而达到cut-set界.

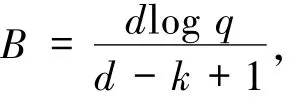
需要注意的是，文献［22］构造的再生码所在的有限域的元素个数是

这个域太大了！最后提出再生码方向两个尚未解决的问题：

1）如何构造“小”域上达到cut-set界的MSR码；

2）研究MSR码的带宽B和域的元素个数q之间的关系.

4 最优极大局部修复码

近年来，在线存储的数据量激增，这导致局部修复码已成为大型分布式存储系统的首选方案.现在考虑一个新的模型，除了考虑单个或少数节点发生故障情况下的局部修复问题，同时还考虑了对最坏情况下更多删除的容错能力［23］.最优极大局部修复码提供了这种局部和整体容错的最佳组合.本节介绍最优极大局部修复码的代数刻画和构造的相关工作.

4.1 最优极大局部修复码的生成阵和校验阵考虑一个分布式存储系统，若该系统由m个不同的元素个数均为r的组所构成，每组内可局部地纠正任意a个删除错误，除此之外整个系统还可额外纠正任意h个删除错误.可以纠正这种分布式存储系统的错误的最优码称为最优极大局部修复码，下面给出最优极大局部修复码的生成阵和校验阵的刻画.

定义4.1设l是素数幂，正整数a、m、r、h满足ma+h＜mr.令n＝mr和k＝n-ma-h.若矩阵

满足如下条件：

2）对于1≤i≤m，Bi可生成［r，r-a，a+1］lMDS码.

3）从每个Bi中删掉a列后，G余下的矩阵生成［n-ma，k，h+1］lMDS码.

则称以G为生成矩阵的l元［n，k］线性码为最优极大（n，r，h，a）l局部修复码（简称为MR（n，r，h，a）l-LRC码）.

根据定义，可直接得到下面的结论.

引理4.1［24］矩阵G＝（B1｜B2｜…｜Bm）∈是MR（n，r，h，a）l-LRC码的生成矩阵当且仅当G的任意一个含有Bi（1≤i≤m）中最多r-a列的k×k子矩阵S是可逆的.

类似地，也可利用校验矩阵给出MR（n，r，h，a）l-LRC码的等价定义.

定义4.2设l是素数幂，正整数a、m、r、h满足ma+h＜mr.令n＝mr和k＝n-ma-h.若矩阵

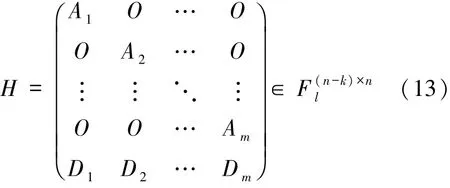
满足以下条件：

2）对于1≤i≤m，Ai可生成［r，a，r-a+1］lMDS码.

3）从每组中任意选择a列后，再任意选择h列，这am+h列Fl-线性无关.

则称以H为校验矩阵的l元［n，k］线性码为MR（n，r，h，a）l-LRC码.

事实上，校验矩阵中的子矩阵Ai是生成矩阵G中子矩阵Bi生成的线性码的校验矩阵.从定义可以看出，最优极大局部修复码的每个部分都是MDS码.类似MDS猜想关于MDS码码长和有限域元素个数之间的关系，很自然地一个问题是：存在l元MR（n，r，h，a）-LRC码的有限域的元素个数l最小是多少？文献［25］讨论了随机码的情形.

引理4.2［25］设l是素数幂，正整数a、m、r、h满足

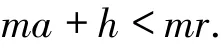
令n＝mr和k＝n-ma-h.若Fl上的随机矩阵G∈以很高概率生成一个MR（n，r，h，a）l-LRC码，则有

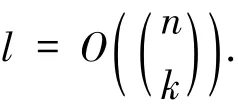
文献［26］等给出了一个下界.

引理4.3［26］设h、a是常数.若2≤h≤n／r，则MR（n，r，h，a）l-LRC码必定满足

4.2 构造最优极大局部修复码很多文献给出了最优极大局部修复码的具体构造.当h≤1时，文献

［27］构造的最优极大局部修复码的有限域元素个数为O（r）.当h＝2，3时，文献［26］构造的最优极大局部修复码的有限域元素个数分别为O（n）、O（n3）.文献［28］利用最大秩距离码的判别准则，从生成阵的角度构造了一类最优极大局部修复码，其有限域元素个数为等［24］从校验矩阵的角度构造了一类最优极大局部修复码，其有限域元素个数为介绍一下文献［28］和［24］的结果.

定理4.1［28］设是MRD码C的生成阵，令对角块矩阵

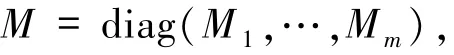
其中Mi是q元［r，r-a］-MDS码的生成矩阵，1≤i≤m，则G＝˜GM是MR（n，r，h，a）l-LRC码的生成矩阵，其中n＝mr，h＝n-ma-k和l＝qN.

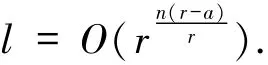
接下来介绍文献［24］中从校验矩阵角度构造最优极大局部修复码的结果.

定义4.3设l是q的幂次，α1，…，αh∈Fl，h阶Moore矩阵M定义为

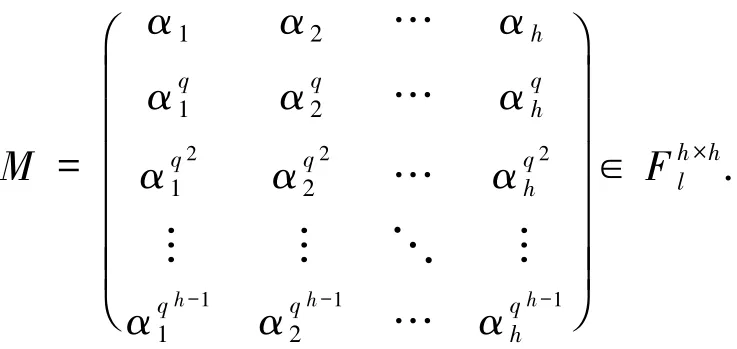
Moore矩阵M的行列式det（M）满足

其中（c1，…，ch）跑遍中全部h-1维线性射影空间中点.

由定义可知，det（M）≠0当且仅当α1，…，αh是Fq-线性无关的.接下来利用Moore矩阵来构造最优极大局部修复码的校验矩阵.设s、m是正整数，记

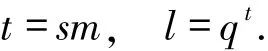
设α11，…，α1s，…，αm1，…，αms是Fl的一组Fq-基.若存在q元［r，r-s，h+a+1］线性码，则对于每个1≤i≤m，存在集合使得βi1，…，βir中任意h+a个元素是Fq-线性无关的.定义Fl上矩阵

利用最优极大局部修复码的校验矩阵的定义和Moore矩阵的性质，可以得到如下结论.

定理4.2［24］设是q元［r，a］MDS码的生成矩阵（1≤i≤m），Di是（14）式定义的矩阵.则以（13）式中的H为校验矩阵的线性码C是MR（n，r，h，a）l-LRC码，且有限域的元素个数是

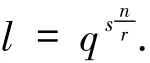
证明因为Ai是［r，a］l-MDS码的生成矩阵（1≤i≤m），所以只需证明定义4.2中的条件3）成立即可.

对于i＝1，2，…，m，设Ti是｛（i，1），（i，2），…，（i，r）｝的子集且｜Ti｜＝a，令Si是｛（i，1），（i，2），…，（i，r）｝＼Ti的子集且

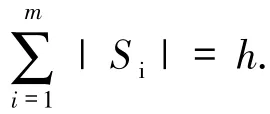
令Ai＝（ai1，…，air），hij是H的第i块的第j列，则

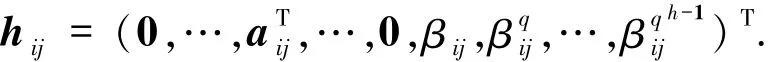
为了证明定义4.2中的条件3）成立，只需证明：对于所有可能的Ti和Si，

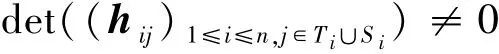
即可.

因此det（（hij）1≤i≤n，j∈T i∪S i）≠0当且仅当矩阵

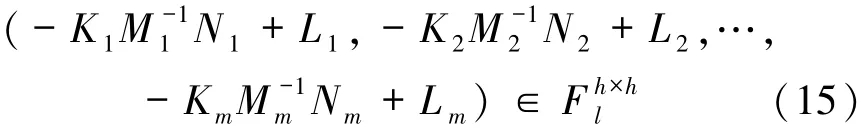
可逆.注意到（15）式给出的矩阵是Moore矩阵，且第一行是

其中μlj∈Fq.设λij∈Fq使得

即

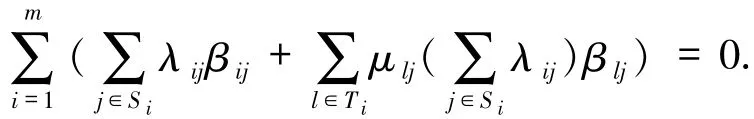
因此对于所有满足1≤i≤m的i都有

因为｛βij｝j∈T i∪S i是Fq-线性无关的，所以λij＝0，j∈Si.因此（16）式中的h个元素Fq-线性无关.故（15）式给出的Moore矩阵可逆，结论得证.

设r，h≥2，整数a满足a≤r.因为Ai是q元［r，a］-MDS码的生成矩阵，所以必有r≤q+1.设q＝2「log2r⏋，则存在q元［r，a］-MDS码和q元［r，r-s，h+a+1］-MDS码，其中s＝h+a.由定理4.2即可得到如下结论.

定理4.3［24］若r≥h+a+1，则存在MR（n，r，h，a）l-LRC码，且域的元素个数是