增广立方体的分支连通度

张其凡，徐丽琼

(集美大学理学院，福建 厦门 361021)

0 引言

互连网络的拓扑结构通常用一个连通图来表示,其中用顶点来代表处理器,边来代表连接线。连通度与边连通度是衡量网络容错性的重要参量。但是，随着大规模网络的不断发展,传统的连通度与边连通度已经不能准确地衡量网络的容错性。利用传统的连通度来衡量网络的容错性有以下3个缺点：首先,对于两个不同的网络,即使它们具有相同的连通度或者边连通度,它们也不一定具有相同的网络可靠性,因为对于不同的网络而言,每条边或每个顶点可能有不同的故障概率；其次,在一个图中删除同样阶数的顶点集或边集,其产生的分支情况可能会有很大的区别，即传统的连通度与边连通度不能准确地衡量网络的损坏程度；最后,在用传统连通度来衡量网络的可靠性时,是在假定一个顶点的所有邻点(或关联这个顶点的所有边)同时出现故障,即最坏情况下评估特定规模网络的可靠性,而这一情况在现实世界里是几乎不可能发生的,因此具有一定的局限性。

为了解决这一参数不足的问题,Harary[1]在1983年提出了条件连通度的概念。而后,Chartrand等[2]和Sapmpathkumar[3]在1984年又分别提出了分支连通度与分支边连通度的概念,它们在本质上就是对传统(边)连通度的推广,因此也可以看作一种条件连通度。一个非完全图G的r分支(边)连通度cκr(G)(cλr(G))指的是在图G中删除最少的顶点(边)数使一个图不连通,并且至少有r个连通分支。其中,cκ2(G)(cλ2(G))就是所研究的传统连通度与边连通度。关于分支连通度,许多互连网络已被研究,包括超立方体[4-5]、折叠超立方体[6]、扭立方体[7]、对偶立方体[8]、交错群图[9]等。

增广立方体是超立方体的众多变形网络中的一种,它不仅保持了超立方的一些优秀属性,比如高对称性和递归性等,而且拥有某些比超立方体更好的性质,比如它的连通度几乎是超立方体的两倍。增广立方体连通度的优越性能吸引了不少专家与学者对其可靠性的广泛研究。基于此,本文主要研究了增广立方体的分支连通度。

1 预备知识

设G=(V(G),E(G))是一个无向连通图,其中V(G)和E(G)分别表示图G的顶点集和边集，用κ(G)表示图G的连通度。对于图G中任意两点u、v，e=uv∈E(G)表示图G中的任意一条边,其中u、v称为边e的端点,边e称为与u、v关联的边。对于图G中任意一个非空顶点集F,用G-F表示从G中删去F中的顶点以及与这些顶点相关联的边所得到的子图。任取图G中的一个顶点u,用NG(u)表示G中与u相邻的所有顶点的集合,记为NG(u)={v∈V(G)：uv∈E(G)},dG(u)=|NG(u)|表示顶点u在图G中的度。对于图G中任意一个非空顶点集S,用|S|表示集合S中元素的个数,用NG(S)表示G中与S相邻的顶点的集合,记为NG(S)=∪v∈SNG(v)S。本文未予定义而直接使用的符号和术语见文献[10]。下面给出一些基本定义、引理及定理。

定义1[11]n维超立方体Qn的点集是定义在集合{0,1}上的n元数组,即V(Qn)={v1v2…vn:ui∈{0,1}}。Qn中的两个顶点u=u1u2…un与v=v1v2…vn之间有边当且仅当u与v的坐标中有且仅有一个不相同。

增广立方体是超立方体的一个变形,其递归定义为定义2。

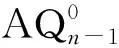
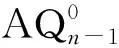
下面也给出n维增广立方体AQn的非递归定义3。

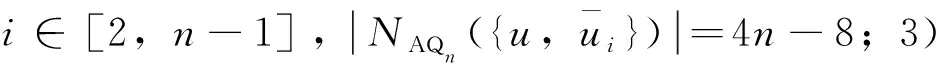
性质2[14]当n≥3时,AQn中的任意两个顶点至多有4个公共邻点。

引理1[13]κ(AQ1)=1,κ(AQ2)=3,κ(AQ3)=4,当n≥4时,κ(AQn)=2n-1。

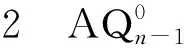
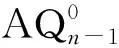
引理4[15]当n≥4时,设F是AQn的顶点子集满足|F|≤4n-9,则AQn-F满足下述条件之一:1)AQn-F是连通的;2)AQn-F有两个分支,其中一个分支是孤立点。

引理5[15]当n≥6时,设F是AQn的顶点子集满足|F|≤6n-18,则AQn-F有一个连通分支H满足|V(H)|≤2n-|F|-2。

引理6[16]当n≥6时,设F是AQn的顶点子集满足|F|≤8n-29,则AQn-F有一个连通分支H满足|V(H)|≤2n-|F|-3。

引理7 当n≥3时,设x、y是AQn中任意两个不相邻的顶点,则|NAQn({x,y})|≥4n-6。

证明根据AQn的定义知,AQn是(2n-1)-正则的。由性质2知,|NAQn(x)∩NAQn(y)|≤4。故|NAQn({x,y})|≥2(2n-1)-4=4n-6。

引理8 当n≥4时,设S是AQn的一个孤立集且满足|S|=3,则|NAQn(S)|≥6n-12。

证明对n进行归纳。当n=4时,易知|NAQ4(S)|≥12,结论成立。假设当n≥5时,结论对n-1维增广立方体成立。下面证明结论对n维增广立方体成立。

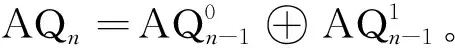
情形1S中的3个顶点属于同一个n-1维增广立方体。

情形2S中的两个顶点属于同一个n-1维增广立方体,另一个顶点属于另一个n-1维增广立方体。

综上可得,当n≥4时,|NAQn(S)|≥6n-12。

引理9 设F是AQ4的顶点子集满足|F|≤9,则AQ4-F至多有两个连通分支。

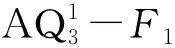
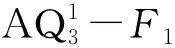
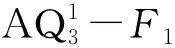
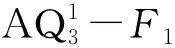
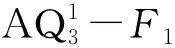
引理10 设F是AQ9的顶点子集满足|F|≤41,则AQ9-F至多有3个连通分支。

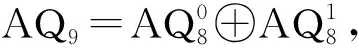
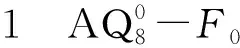
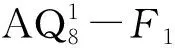
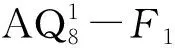
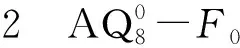
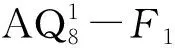
2 主要结果及其证明

定理1 当n≥4时,设F是AQn的顶点子集满足|F|≤4n-7,则AQn-F至多有两个连通分支。

证明对n进行归纳。当n=4时,由引理9知结论成立。假设当n≥5时,结论对n-1维增广立方体成立。下面证明结论对n维增广立方体成立。

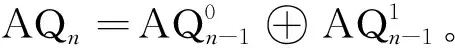
定理2 当n≥9时,设F是AQn的顶点子集满足|F|≤6n-13,则AQn-F至多有3个连通分支。

证明对n进行归纳。当n=9时,由引理10知结论成立。假设当n≥10时,结论对n-1维增广立方体成立。下面证明结论对n维增广立方体成立。

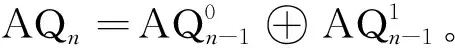
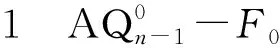
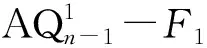
子情形1 |F1|≤4n-11。

子情形2 |F1|=4n-10。

定理3 当n≥4时,cκ3(AQn)=4n-6。

证明首先通过在AQn中构造一个3-分支割集F满足|F|=4n-6来证明cκ3(AQn)≤4n-6。

下面要证明cκ3(AQn)≥4n-6。由定理1知,当n≥4时,所有的3-分支割集的大小都要大于4n-7。根据3-分支连通度的定义知,cκ3(AQn)≥4n-6。

综上可得,当n≥4时,cκ3(AQn)=4n-6。

定理4 当n≥9时,cκ4(AQn)=6n-12。

证明通过在AQn中构造一个4-分支割集F满足|F|=6n-12来证明cκ4(AQn)≤6n-12。

下面要证明cκ4(AQn)≥6n-12。由定理2知,当n≥9时,所有的4-分支割集的大小都要大于6n-13。根据4-分支连通度的定义知,cκ4(AQn)≥6n-12。

综上可得,当n≥9时,cκ4(AQn)=6n-12。

3 结论

本文主要从分支连通度研究了增广立方体的容错性,要使得增广立方体不连通并且至少有3个连通分支,至少要从增广立方体中删去4n-6个顶点；要使得增广立方体不连通并且至少有4个连通分支,至少要从增广立方体中删去6n-12个顶点。本文研究的是特殊情况,而对于一般情况,即：若要使得增广立方体不连通并且至少有k个连通分支,至少要删去多少个顶点？这是接下来该考虑的问题。