Cahn-Allen方程的精确解

时倩倩,刘法贵

(华北水利水电大学 数学与统计学院，河南 郑州 450046)

近年来，相变理论中相场模型的相关研究备受瞩目。由于其数学内涵的丰富性及复杂程度，加上其在材料科学中的应用，故相场模型的研究无论是在理论上还是在实际上都有意义。相场理论的基本模型有4种：Cahn-Allen方程、Cahn-Hillard方程、Penrose-Fife系统、Cagnalp系统。其中，Cahn-Allen方程为

ut-uxx+u3-u=0。

(1)

随着科学技术的不断发展，人们采用直接积分法[1]、试探函数法[1-2]、齐次平衡法[3]、简单方程法[4]、(G′/G)-展开法[5]、广义双曲正切-余切法[6]等成功求解了不同类型的非线性偏微分方程。文献[5]应用(G′/G)展开法求出了Cahn-Allen方程的精确解,所得结果包含周期解和孤波解。文献[6]使用广义双曲正切-余切法对分数阶Cahn-Allen方程进行了研究，求出了非线性分数阶Cahn-Allen方程的行波解。

本研究使用试探函数法和齐次平衡法来求方程(1)的精确解,得到其扭状孤立波解。通过引入试探函数，将其代入原方程获得关于参数的一组方程，由于求解过程相对烦琐，故需要借助Mathematica软件。

1 试探函数法求精确解

引入函数变换

u(x，t)=φ(ξ)，ξ=x-ct，

(2)

式中：c为波速。由式(1)、(2)，经计算得

-cφ′-φ″+φ3-φ=0。

(3)

假设方程(3)具有如下形式的解:

(4)

式中：a、A、B为待定常数。由式(4)直接计算可得

(5)

(6)

将式(4)、(5)、(6)代入方程(3)，可得

-cAa(y+y2)-Aa2(y-y2)+A3y3+3A2B(y2+y3)+3AB2y(1+y)2-
Ay(1+y)2+(B3-B)(1+y)3=0，

(7)

式中：y=expaξ。由1、y、y2、y3的线性无关性，得到关于参数a、A、B的代数方程组：

(8)

对方程组(8)求解,得

于是，求得方程(3)的精确解为

(9)

(10)

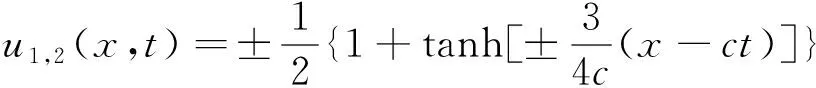
2 齐次平衡法求精确解

为使方程(1)中的最高阶导数项和非线性项部分平衡，假设方程(1)具有如下形式的解：

u=fx(φ)+r。

(11)

下面将确定函数f(φ)和φ(x，t)，以及常数r，使式(11)满足方程(1)。将式(11)代入方程(1)的左边，得

(12)

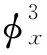
f′3-f‴=0。

(13)

该方程有解

(14)

从而得

(15)

利用式(13)，得

(16)

在式(16)中置f″、f′的系数和常数项为0，可得φ和r满足方程组

(17)

和

r3-r=0。

(18)

从式(18)中解出

r=1，r=-1，r=0。

(19)

取r=1，则方程组(17)变为

(20)

假设

φ=1+exp(kx+αt)，

(21)

式中：k和c为待定常数。将式(21)代入(20)，可知待定系数k和c满足

(22)

求解式(22)，得到

(23)

将式(21)、(23)及r=1代入式(11)中，可得

(24)

取r=-1，类似讨论，可得方程(1)的另一个孤立波解

(25)

取r=0，可同样得到式(24)、(25)。

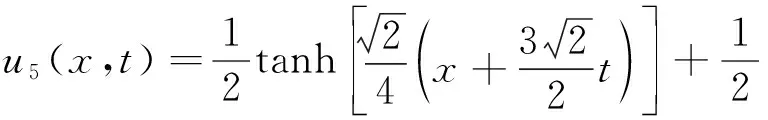
由定理1和定理2可以看出，虽用不同的方法，仍得到了具有相同函数形式的扭状孤立波解。

3 定性分析

令x=φ(ξ)、y=φ′(ξ)，则式(3)等价于

(26)

方程(26)有3个奇点O(0，0)、A(1，0)和B(-1，0)。对于奇点O,注意到方程(26)对应的线性系统特征根满足λ2+cλ+1=0。因此，当c<0时，O是不稳定的奇点，而当c>0时，O是稳定的奇点。对于奇点A、B,注意到方程(26)对应的线性系统特征根满足λ2+cλ-2=0。因此，A、B是不稳定的奇点。

对于方程(26)，由于Px+Qy=-c，故由Bendixson判据，可以断定如下结论成立:

定理3当c≠0时，方程(13)在全平面上不存在闭轨线，即此时方程(1)不存在钟状的孤立波解和周期行波解。

4 结语

本研究运用试探函数法、齐次平衡法求解Cahn-Allen方程，得到了具有相同形式的扭状孤立波解。并且，进行定性分析得到当c≠0时，方程(1)不存在钟状的孤立波解和周期行波解。由此可见，试探函数法和齐次平衡法是求解非线性发展方程的有效方法。