立足数学实验 积累活动经验 发展理性思维——以“三角形内角和定理（第1 课时）”为例

林运来

（厦门大学附属实验中学，福建 漳州 363123）

一、内容及解析

（一）内容

本节课选自北师大版《义务教育教科书·数学》八年级上册第七章第5 节“三角形内角和定理”（第1 课时），主要内容为探索并证明三角形内角和定理，以及应用该定理解决简单的问题.

（二）内容解析

三角形是初中数学研究的重要几何图形之一，也是学生深入、系统研究的第一个几何图形.三角形作为最简单的封闭图形，是研究几何的重要基础［1］，本节课作为“三角形内角和定理”的第一节课，具有承前启后的作用.教学中，通过引导学生回顾探究与验证“三角形内角和等于”的实验过程，立足学生已有的数学活动经验，获取证明思路，鼓励学生寻求多样的证明方法，并在多样的证明方法中感受其共性.通过本节课的学习，将深化学生对三角形的认识，让学生认识到说话办事要有根有据，体会到证明活动是探索活动的自然延续和必要发展，对于观察、实验、归纳得到的结论一定要给予证明，从而提升思维能力，发展核心素养.

本节课的教学重点：对三角形内角和定理证明的必要性的认识和理解；证明三角形的内角和定理，并进行简单的应用.

教学难点：三角形内角和定理的证明方法.

二、目标和目标解析

（1）经历三角形内角和定理的探索与证明过程，进一步发展推理能力.

（2）证明三角形内角和定理，并会应用该定理解决简单的问题.

（3）在一题多解、一题多变中，积累解决几何问题的经验，提升数学思维能力.

（4）初步掌握证明的规范性，逐步养成步步有据的习惯，形成严谨的科学态度.

三、教学问题诊断分析

学生在生活中广泛接触过三角形及其应用，具备一定的生活经验.在小学阶段学生已经学习过“三角形的内角和等于180°”，七年级学生又通过活动再次验证了这一结论，具备一定的知识基础.上述学习过程，让学生掌握了一定的方法基础.但学生对于证明意义的理解和证明过程中格式的规范性尚未掌握，对“理性思维”的认识有待提升.

《义务教育数学课程标准（2011 年版）》指出：“学生是数学学习的主体，在积极参与学习活动的过程中不断得到发展.”［2］在教学中，教师引导学生把握每个环节的探索任务，利用数学工具动手操作、动脑思考，积极参与到数学活动中，积累数学基本活动经验，从感性到理性掌握数学命题，不断提升实践能力.

四、教学媒体设计

通过黑板板书知识框架和研究思路，“使学生更好地把握教学内容的脉络”；通过PPT 展示课件内容；通过屏幕展示学生的学生成果；利用三角形纸片、三角板、量角器等教具展示有关结论的探索、发现过程.

五、教学过程

（一）温故知新，树立证明意识

教师活动：（PPT 展示）费马的失误

形如22n+1（n为自然数）的数称为费马数，简记为Fn.1640 年，法国数学家费马根据F0=3，F1=5，F2=17，F3=257，F4=65537 都是质数做出猜想：对于所有的自然n，Fn均为质数.

直到1732 年，瑞士数学家欧拉指出F5=641×6700417 不是质数，从而否定了费马的猜想.

问题1：从中你能得到什么启示？

生：通过观察、实验、归纳得到的结论可能正确，也可能不正确.

师：是的，归纳推理和演绎推理都是数学研究的有效工具.但是，基于简单操作生成的结论未必可靠，需要严格推理论证后方可推广使用.［3］

［设计意图］引领学生回顾旧知，为本节课的学习做好铺垫，唤醒学生对证明必要性的感受和证明意识的建立，帮助学生形成反思质疑等良好的学习习惯.

（二）数学实验，探索几何结论

教师活动：在黑板上作出△ABC.

问题2：大家说一说学过的三角形的相关知识.

生1：△ABC有三个顶点A，B，C，三条边AB，BC，CA，三个内角∠A，∠B，∠C.

生2：AB+BC>AC，AB+AC>BC，BC+CA>BA.

生3：三角形的内角和等于180°，也就是∠A+∠B+∠C=180°.

师（追问）：事实上，我们在小学就已经知道，任意一个三角形的内角和等于180°.你还记得我们是怎么发现这个结论的？

生3：通过度量或剪拼的方法得出这一结论的.

［设计意图］通过追问，引出“度量或剪拼”的探索方法，唤醒学生相关数学基本活动经验.

实验1：我们手上有一副三角板（如下图），用量角器测量每个三角板的三个角的大小，并计算它们的和.

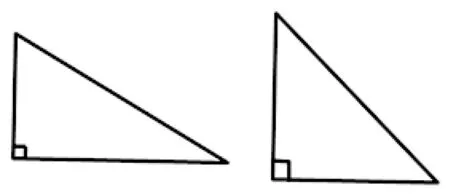
学生活动：按要求用量角器测量三角形的三个角的角度，然后把三个角度加起来.

实验2：在准备好的三角形纸片顶点处标上字母A，B，C，将三角形纸片的∠B和∠C剪下来，分别与∠A拼合在一起（顶点重合，三个角不重叠）.

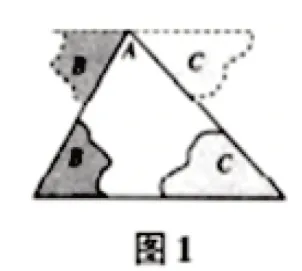
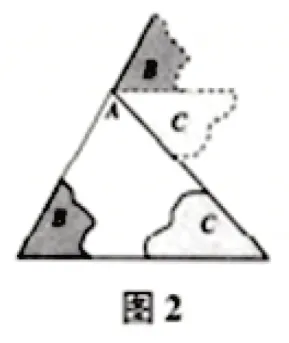
学生活动：按要求进行剪拼，并将剪拼结果贴到黑板上，如图1、图2 所示.

师（追问）：你有什么发现？

生4：在图1、图2 中，可以发现三个角合起来形成一个平角.

师：另取一张三角形纸片，与实验2 一样进行标注，剪下∠C，将其与∠A（或∠B）拼合在一起，你有什么发现？

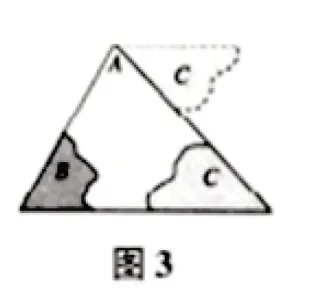
学生按要求活动，教师不急于做出判断，而是引导学生探索不同的拼合方法，并从中找出能用前面所学知识证明“三角形的内角和等于180°”的拼图，将其贴在黑板上，如图3 所示.

［设计意图］借助工具让学生动手操作、动脑思考，自主探索数学知识，从而经历知识的形成过程，“让思维可见”.同时通过引导学生经历从不同角度寻求分析问题、解决问题的过程，体验解决问题方法的多样性［2］.

（三）内化知识，创设推理情境

师：上面我们经过测量和剪拼实验后，大家得出了共同的结论：三角形的内角和等于180°.但是，形状不同的三角形有无穷多种，我们才测量了几个三角形，才剪拼了几种三角形，而仅仅通过测量和剪拼了全体三角形中的极小极小的一部分，何况“测量常常有误差”“剪拼后观察不一定细致”，这就会导致得出的结论不一定正确，不能完全让人信服.因此，要确定对所有的三角形而言，它的内角和一定是180°，我们怎么办呢？

生5：需要证明这个结论.

师：很好！在几何学里，只有从公理和定义出发，经过演绎推理而证明了的命题，才被认为是真理.归纳推理被赶出了几何的花园.［4］

师（继续）：虽然测量、实验所产生的“结论”不一定正确，但它是我们发现数学公式、定理的重要途径，有时也能为我们证明结论提供方法指引.

问题3：回顾上面的实验2，说说实验中剪拼角的目的是什么？从中能得到什么样的启发呢？

生6：图1 中，剪拼的过程，相当于将∠B，∠C都移到∠A处，图2 和图3 也有同样的效果.证明时，我们可以通过作平行线，实现这种平移效果.

问题4：大家观察图1、图2 和图3，在这三幅图中，是否存在一条与△ABC的边BC平行的直线？

师生活动：学生认真观察并分析，教师引导学生对实验的拼图结果进行抽象，得到图4、图5 和图6.

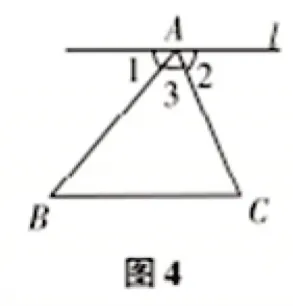
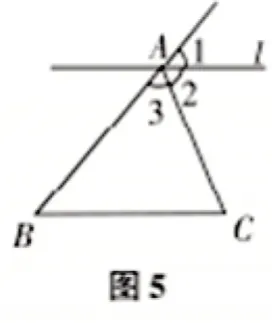
［设计意图］引导学生回顾探索与验证过程，归纳实验成果，从中获取证明的思路，为证明结论做好铺垫.通过引导学生对实验成果进行抽象，创设推理情境，“让思维可见”，有助于把握数学问题的本质，达到优化解题的目的，培养数学抽象、逻辑推理等数学学科核心素养.

（四）教师示范，注重答题规范

例1 已知：如图7，△ABC.

求证：∠A+∠B+∠C=180°.

教师活动：与学生交流图4 中辅助线的作法，并结合图形向学生“示范”推理过程.

证明：如图4，过点A作直线l，使l∥BC，则∠B=∠1（两直线平行，内错角相等），∠C=∠2（两直线平行，内错角相等）.

因为∠1+∠2+∠3=180°（平角的定义），

所以∠BAC+∠B+∠C=180°（等量代换）.

［设计意图］教师条理清晰地板书推理论证过程，以便学生“临摹”与“借鉴”，这样学生在遇到陌生的问题和领域时，就有章可循，有法可依.

问题5：你还能根据图5 或图6，用其他方法证明三角形内角和定理吗？

教师活动：利用投影展示学生的推理过程.

生7：如图5，延长BA，过点A作直线l∥BC，则

∠1=∠B（两直线平行，同位角相等），

∠2=∠C（两直线平行，内错角相等）.

因为∠1+∠2+∠3=180°（平角的定义），

所以∠BAC+∠B+∠C=180°（等量代换）.

生8：如图6，过点A作直线l∥BC，则

∠1=∠C（两直线平行，内错角相等），

∠1+∠2+∠B=180°（两直线平行，同旁内角互补）.

所以∠BAC+∠B+∠C=180°（等量代换）.

师：上面我们用几种不同的方法证明了“三角形的内角和等于180°”，这就是三角形内角和定理.

［设计意图］鼓励学生寻求多样的证明方法，有助于激活学生的数学思维，达到举一反三的效果.在一题多解、一题多变中，积累解决几何问题的经验，提升解决问题的能力.［5］在学生思考的基础上，教师要求学生写出严格的证明过程，最后进行展示、交流、评析，矫正学生的典型错误.

问题6：上面的几种证明方法可谓“殊途同归”，都圆满地证明了三角形内角和定理，你能说说这几种证明方法有什么共同的特点吗？

生9：通过作平行线，利用平行线的性质，将部分角移到适当的位置，使分散的三个角相对集中，从而解决问题.

［设计意图］引导学生比较不同的解法，同时在多样的证明方法中感受共性：利用辅助线，实施平移变换，将分散的要素集中起来.

（五）运用新知，解决简单问题

例2 如图8，在△ABC中，∠B=38°，∠C=62°，AD是△ABC的角平分线，求∠ADB的度数.

解：在△ANC中，

∠B+∠C+∠ABC=180°（三角形内角和定理）.

因 为∠B=38°，∠C=62°（已知），

所 以∠BAC=180°-38°-62°=80°（等式的性质）.

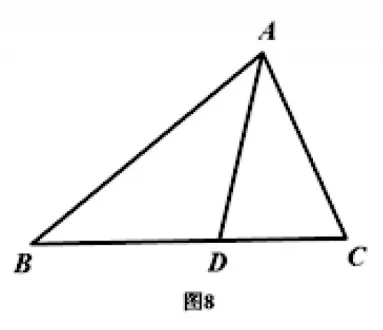
因为AD平分∠BAC（已知），所以∠BAD=∠CAD=∠BAC=40（°角平分线的定义）.

在△ADB中，

∠B+∠BAD+∠ADB=180°（三 角 形 内 角 和 定理）.

所 以∠ADB=180°-∠B-∠BAD=180°-38°-40°=102°（等式的性质）.

师生活动：教师讲解例1，学生独立完成例2 以及教材179 页“随堂练习”1、2、3 题，教师提问学生并及时评价.

（六）反思小结，提升学科素养

问题7：请同学们想一想：

（1）本节课我们学习了哪些知识内容？

（2）你认为证明“三角形的内角和等于180°”有什么意义？

（3）在应用“三角形的内角和等于180°”这一结论解决问题时应注意些什么？

师生活动：学生短暂梳理，小组代表发言，教师总结.

［设计意图］该环节既有学生的分享交流，又有教师的总结提炼，引导学生从知识和方法两个层面关注本节课的收获，为后继学习做铺垫.

（七）设计板书，突出研究思路

本节课的板书如图9 所示.

图9

六、教学目标检测

（一）检测形式：课后作业.

（二）检测内容：

1.△ABC中，∠C=90°，那么∠A+∠B______.

2.在一个三角形中最多有几个钝角？为什么？

3.△ABC中，∠B=∠A+10°，∠C=∠B+10°.求△ABC的各内角的度数.

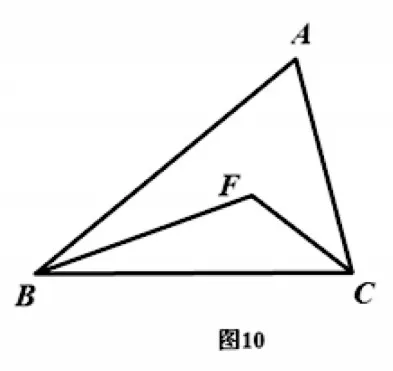
4.如 图10，在△ABC中，BF平分∠ABC，CF平分∠ACB，∠A=65°，求∠F的度数.

七、教学反思

（一）创设合适的问题情境，激发学生数学思考

合适的问题情境有助于引发学生思考与交流，形成和发展数学核心素养，也为学生数学核心素养提供了真实的表现机会.［6］本节课的多个环节，教师非常重视学生的主体地位，精心创设问题情境，如引导学生从“费马的失误”的故事中认识到数学需要证明，对数学学习和生活中的其他事物，也应养成追究其缘由、问个为什么的习惯；再如，引导学生由剪拼实验创设推理情境，引导学生把握数学内容的本质等.通过在数学对象发生发展的关节点上创设合适的教学情境，不仅能启发学生思考，更关键的是能够引导学生开展数学探究活动，真正让学生成为学习活动的主角.

（二）重视证明的规范性，发展学生推理能力

“教育就是培养良好的学习习惯”，学生推理能力的发展应贯穿于整个数学学习过程中.本节课的教学中，教师首先引导学生回顾探索“三角形内角和等于”的数学实验，感悟合情推理是数学研究的有效工具；其次，引导学生立足数学实验、借助图形直观地探索证明思路，体验发现结论到验证结论的过程；再次，借助规范的板书进行示范，做到步步有据，在这个过程中引导学生学会数学思考、感悟理性精神；最后，引导学生探索证明结论的不同思路和方法，解决问题，获得成就感，增强自信心，发展思维的广阔性和灵活性.这样的数学学习，使学生亲历数学知识的建构过程，既掌握了基础知识和基本技能，又获得了基本思想和基本活动经验.

密立根说过：“科学靠两条腿走路，一是理论，一是实验，有时一条腿走在前面，有时另一条腿走在前面，但只有使用两条腿，才能前进.”在数学实验教学中，立足基础，突出实验操作，可以提升学生的学习力，引导学生发现问题并探寻解决之道.要放手让学生去探究，变结果性知识为过程性知识，培养学生的信息获取能力、分析论证能力和问题解决能力，树立敢于质疑、善于思考、严谨求实的科学精神，引领学生从“学会”走向“会学”，最终促进学生的数学核心素养的发展.