修正Bernstein 算子加Jacobi 权的Voronovskaja 型估计

夏荣荣，虞旦盛

（杭州师范大学 数学系，浙江 杭州310036）

记C[0，1]为［0，1］上连续函数的全体，对任意的f(x) ∈C[0，1]，著 名 的 Bernstein 算 子 定 义 为x)n−k，k=0，1，2，…，n；n=1，2，…。 Bernstein 算子对连续函数逼近的研究已非常广泛［1-2］。ZHOU［3］证 明 了Bernstein 算 子 在 加Jacobi 权w(x)=xa(1−x)b，0 ＜a，b＜1 时 是 无 界 的(C，‖⋅‖w，这里‖f‖w=：‖wf‖C[0，1])。为解决此问题，ZHOU［3］引 入 了 一 种 新 的 范 数 ‖f‖w=：算 子在此范数下是有界的。之后，很多学者致力于研究Bernstein 算子在该范数下的加权逼近，但这些加权逼近结果大多只针对连续函数，而且权函数中的参数一般有上下界限制（要求0 ＜a，b＜1），当目标函数具有奇性时（如，经典的Bernstein算子可能无定义，不能用以逼近此类函数。

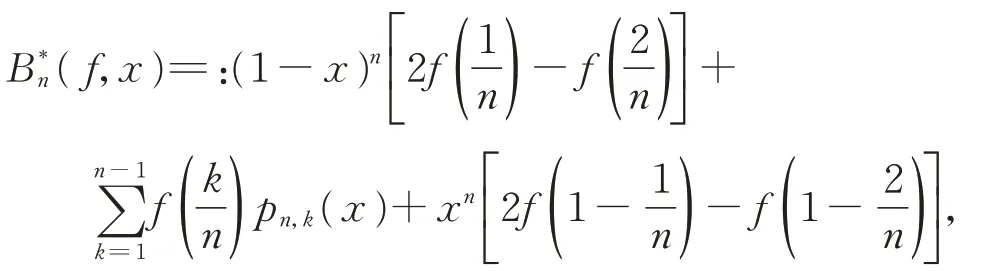
对于f(x) ∈Cw，定义加权光滑模

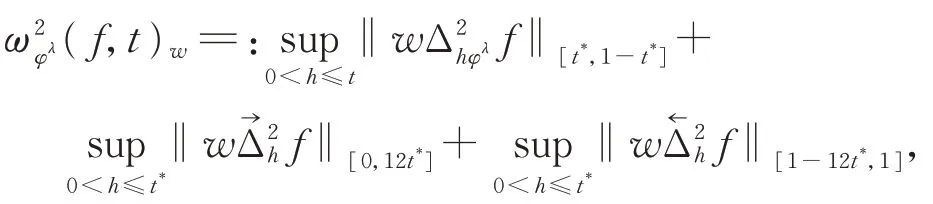
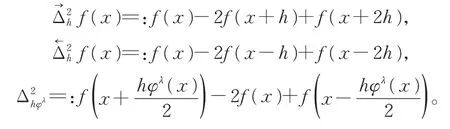
VECCHIA 等［4］建立了下列逼近正定理：

定理1对于任意的a，b＞0，有

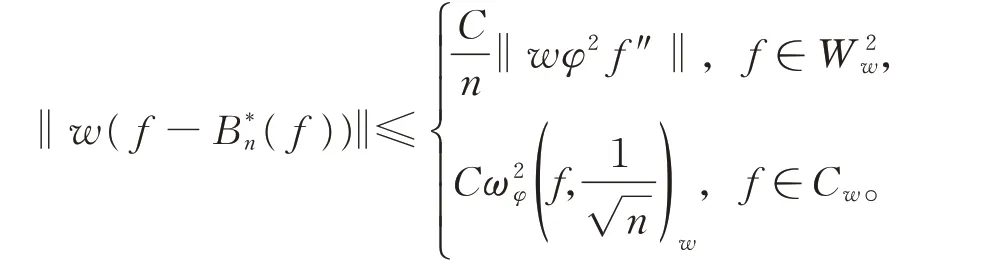
WEI 等［5］改进了上述定理，建立了下列点态逼近定理：

定 理 2对 于 任 意 的a，b＞0，0 ≤λ≤1，f∈Cw，有

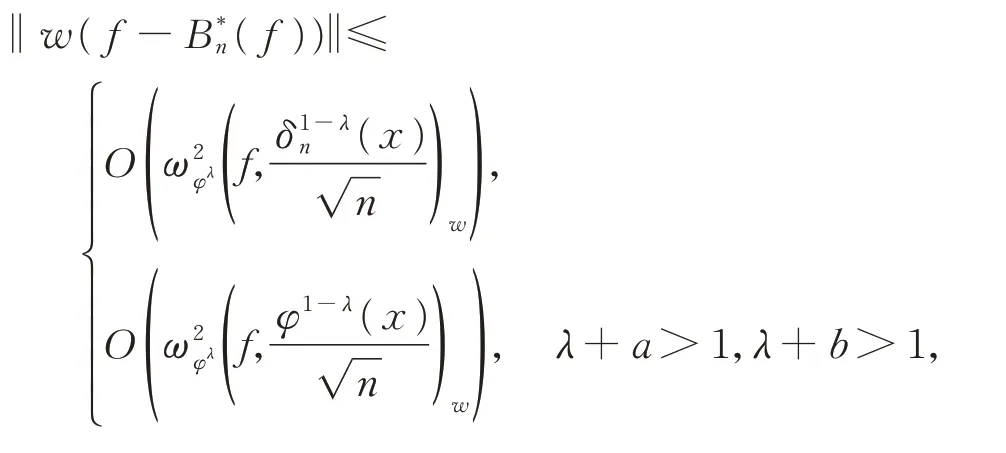
有关修正Bernstein 算子对具有奇性函数的加权逼近研究的部分工作可参见文献［6-11］。

本文的主要目的是建立(f，x)在加Jacobi 权w(x)=xa(1−x)b下的Voronovskaja 型估计。主要结论如下：

定 理3如 果f(x)∈Cw，0 ≤λ≤1，w(x)=xa(1−x)b，那么对于任意的a，b＞0，存在仅依赖于λ，a，b的常数C，使得

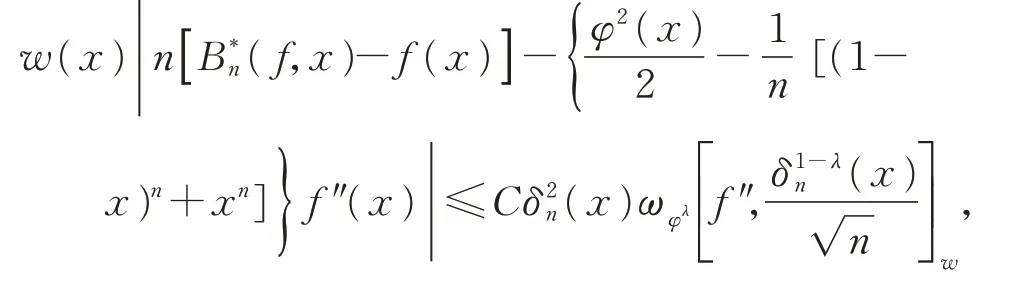
其中，

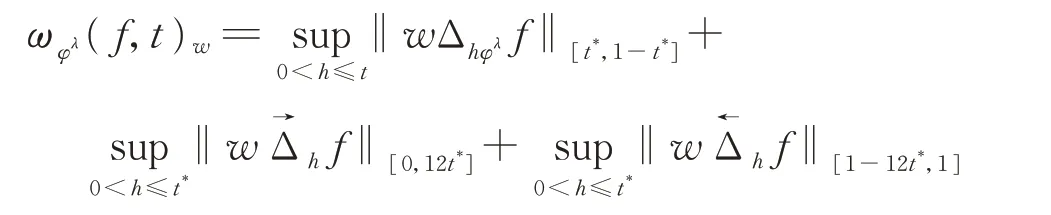
文中，C表示仅依赖于λ，a以及b的常数，在不同的地方可取的不同值。

1 引 理

引 理1记∞}，0 ≤λ≤1，a，b＞0，则对于任意的x∈(0，1)，有

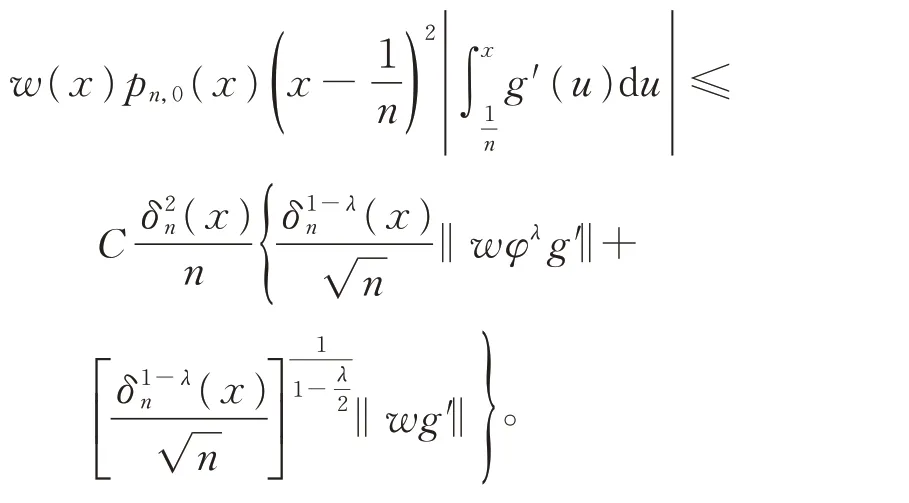
证明分以下2 种情形。

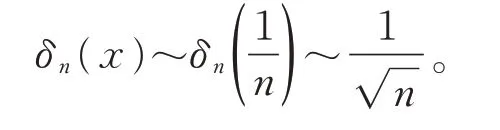
因此有

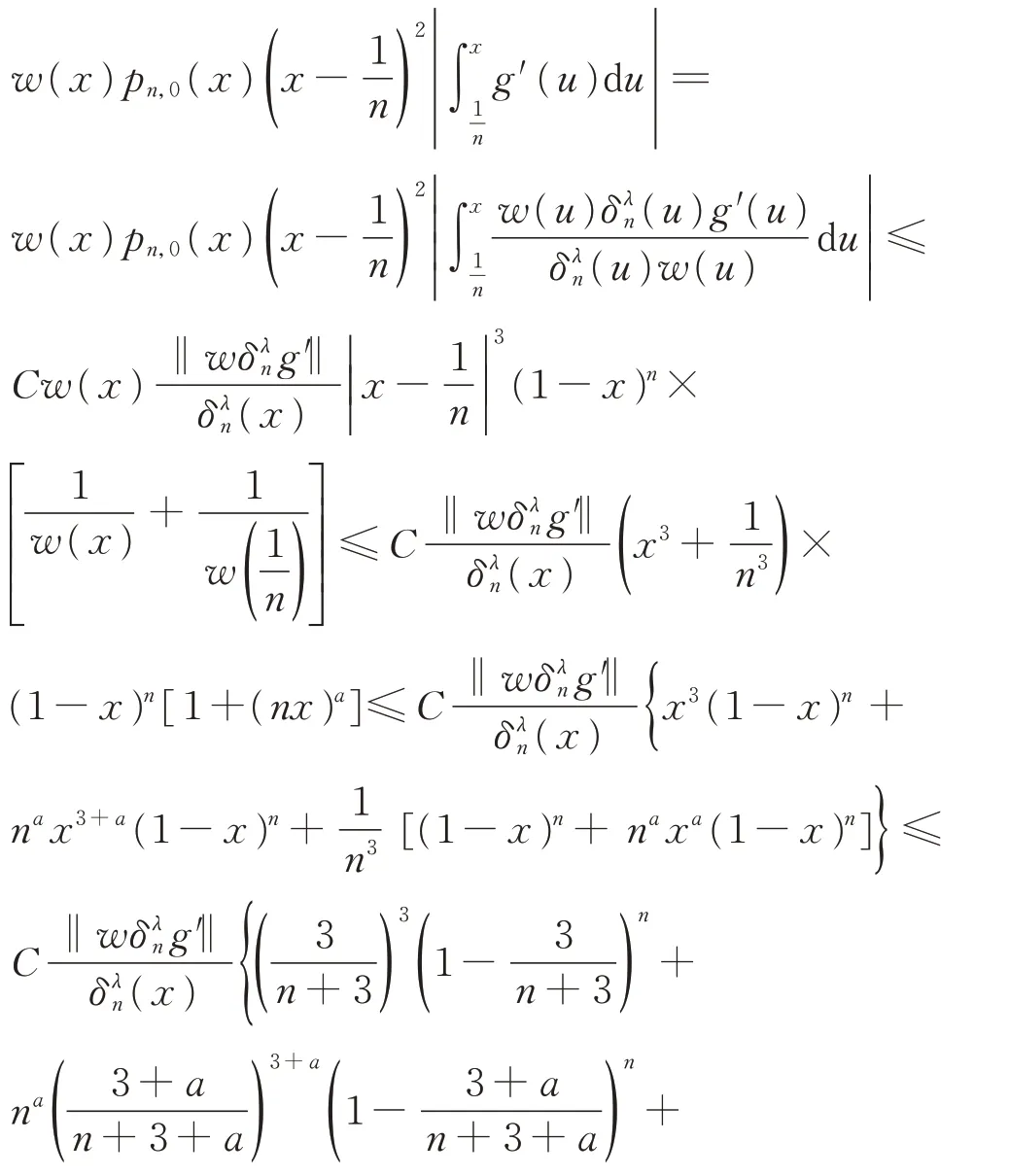
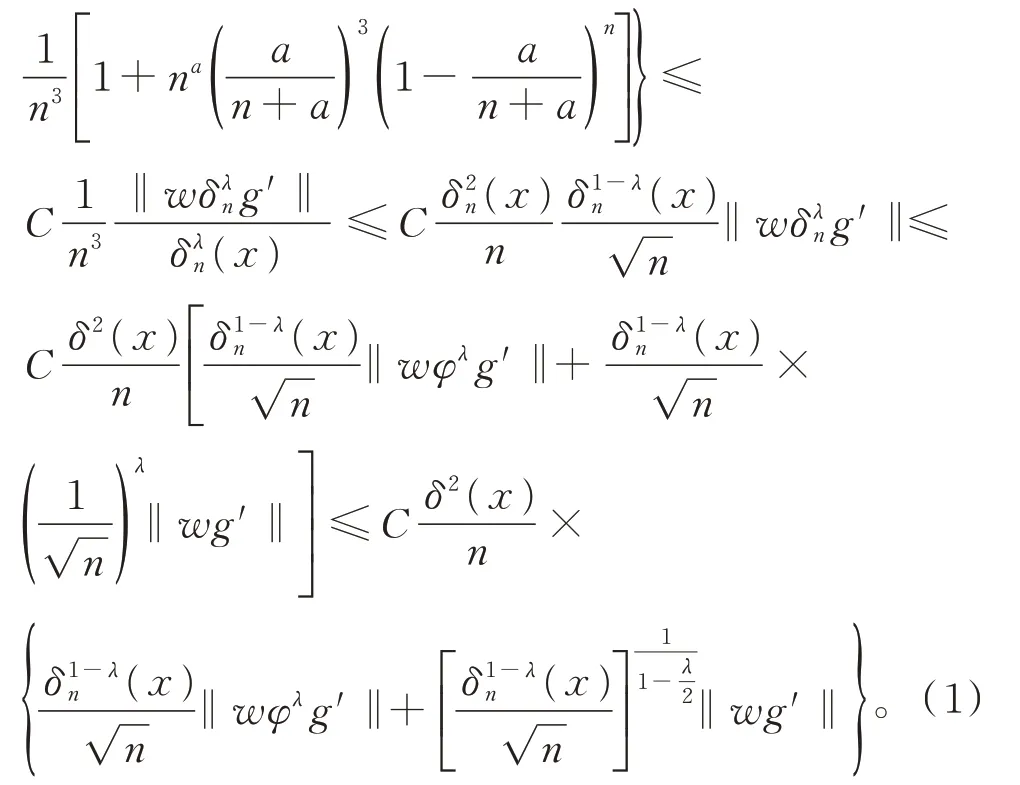
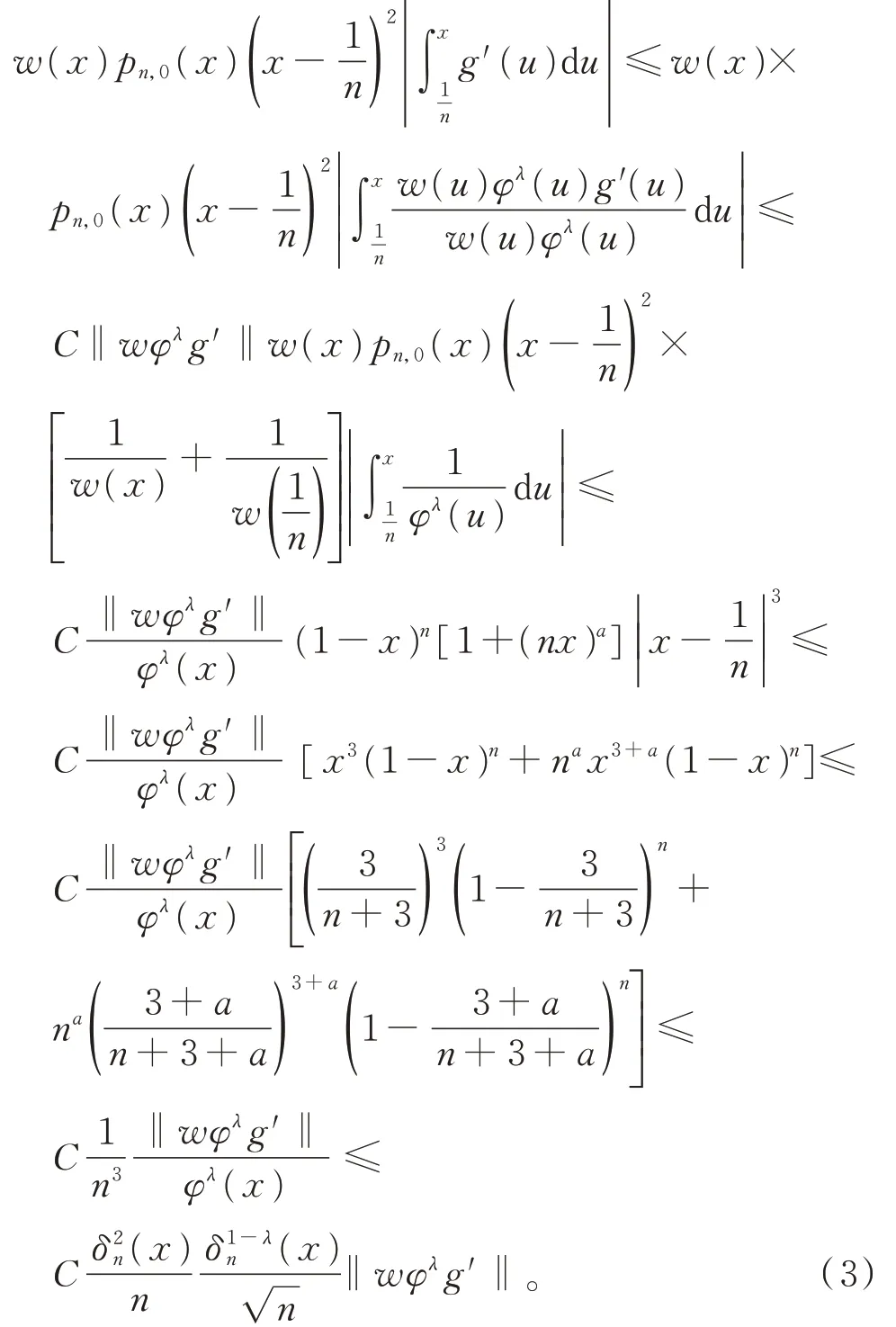
结合式（1）和式（3），引理1 得证。

引理2若f″(x) ∈Cw，则有

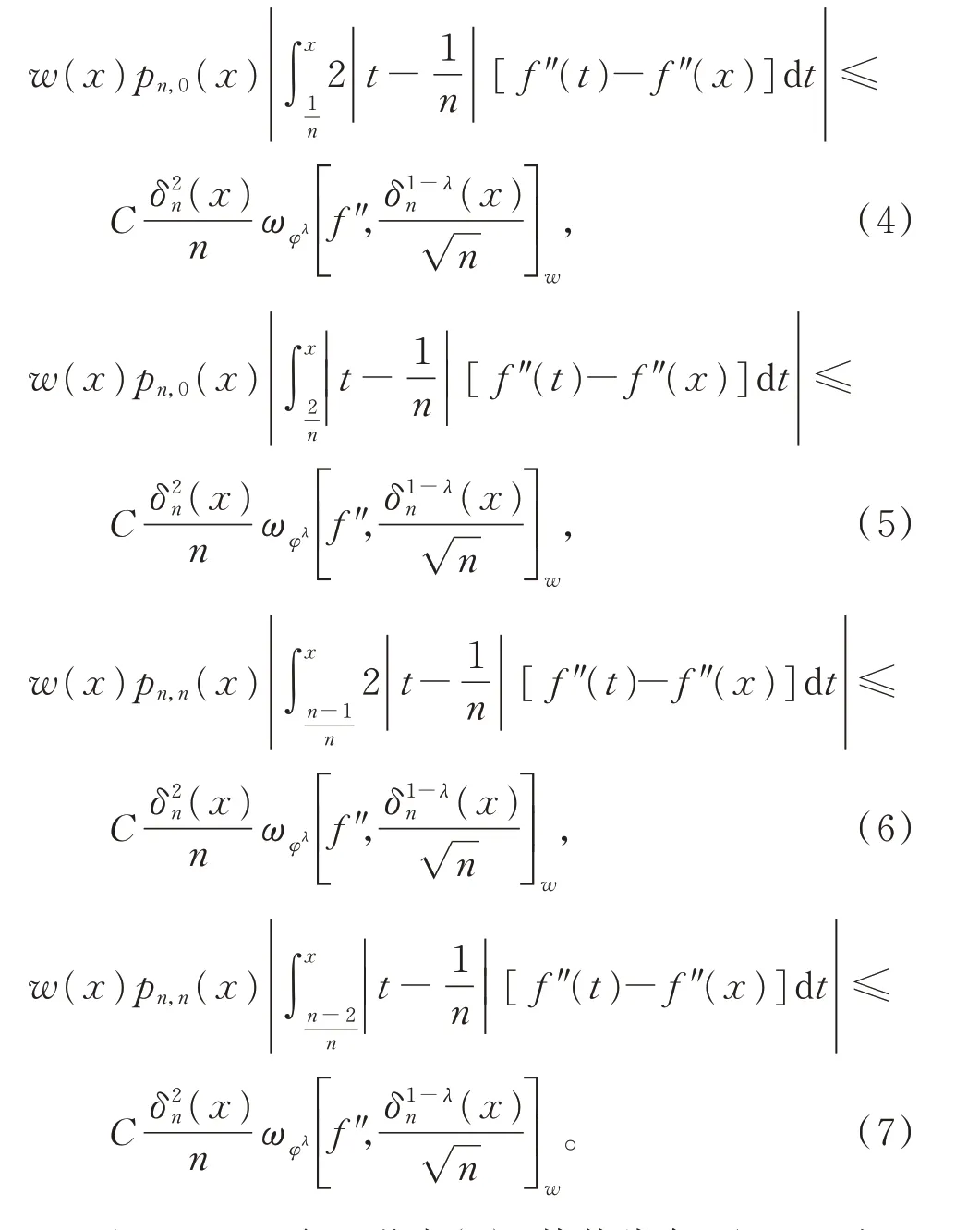
证明只需证明式（4），其他类似可证。对于f(x)∈Cw，定义K-泛函：

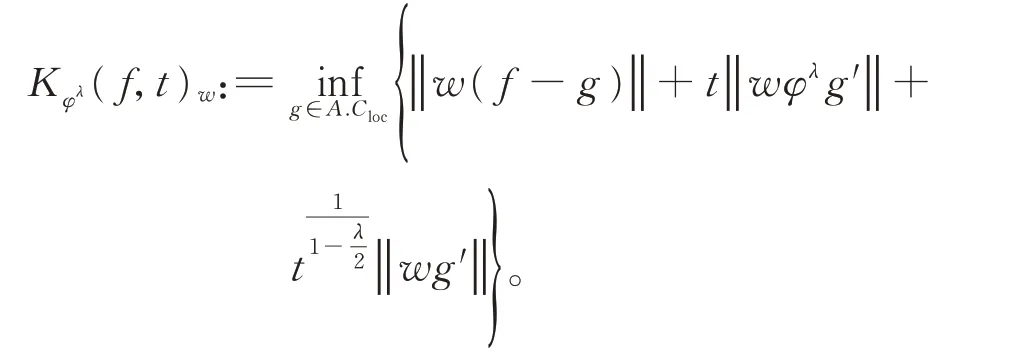
则有［12］

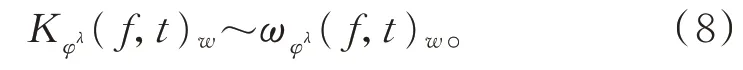
由式（8）知，存在g∈A.Cloc，使得

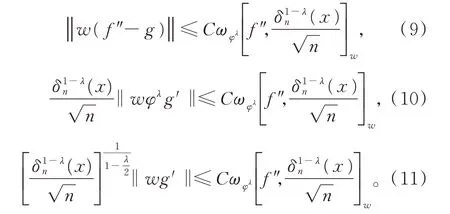
分解式（4）左侧，有

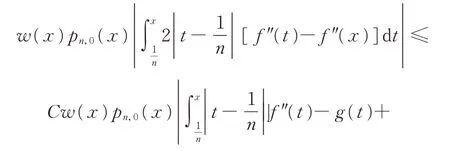
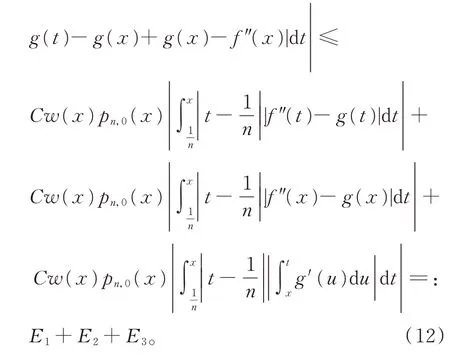
对任意的介于x和之间的t，有［1］

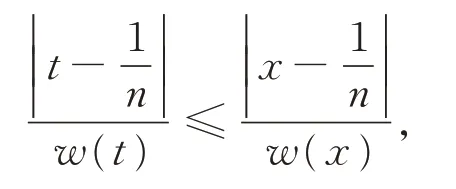
以及

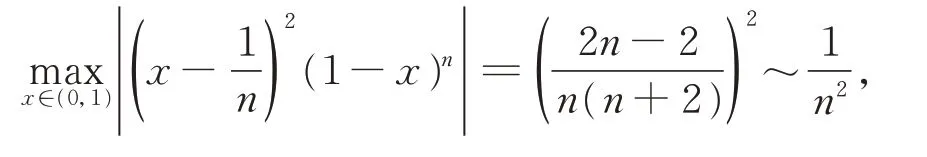
即

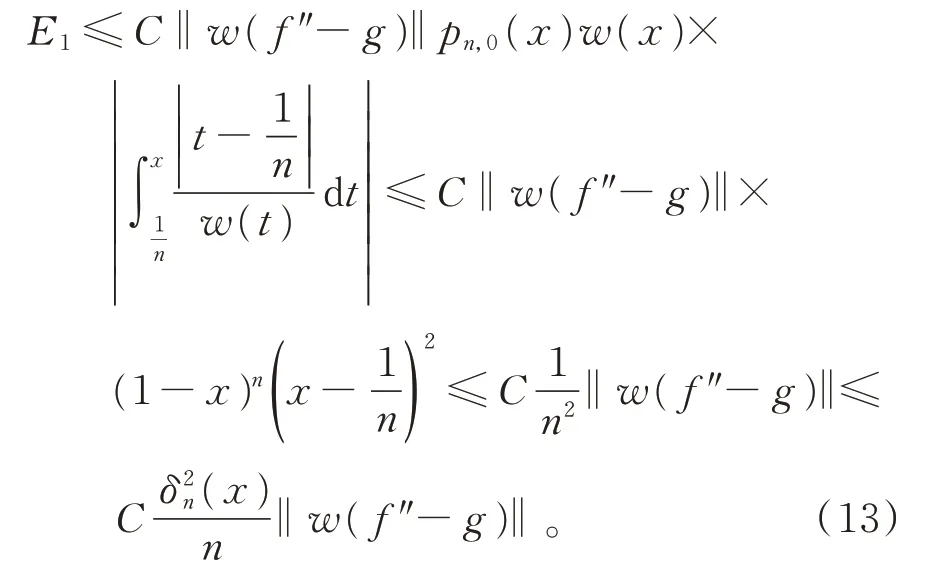
类似地，有

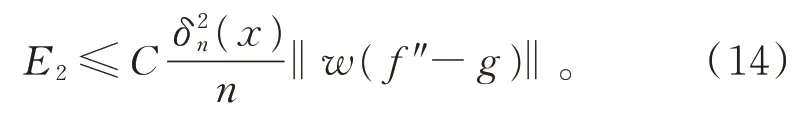
下面估计E3。由引理1 知，

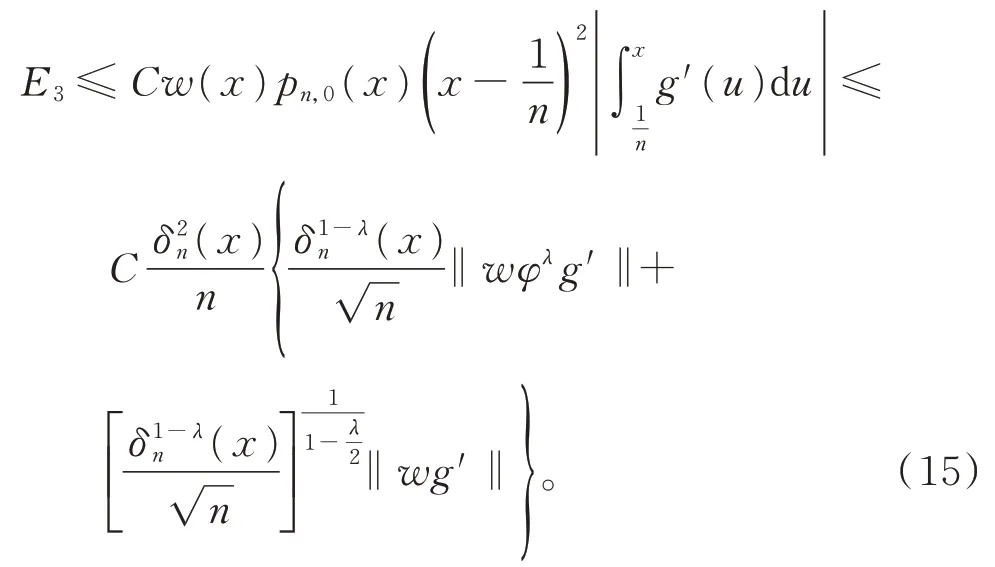
结合式（9）～式（15），式（4）得证。

引 理 3对 于g(x)∈Dλ：={g(x)∈A.Cloc，‖φλ g′‖＜∞}，x∈(0，1)，有

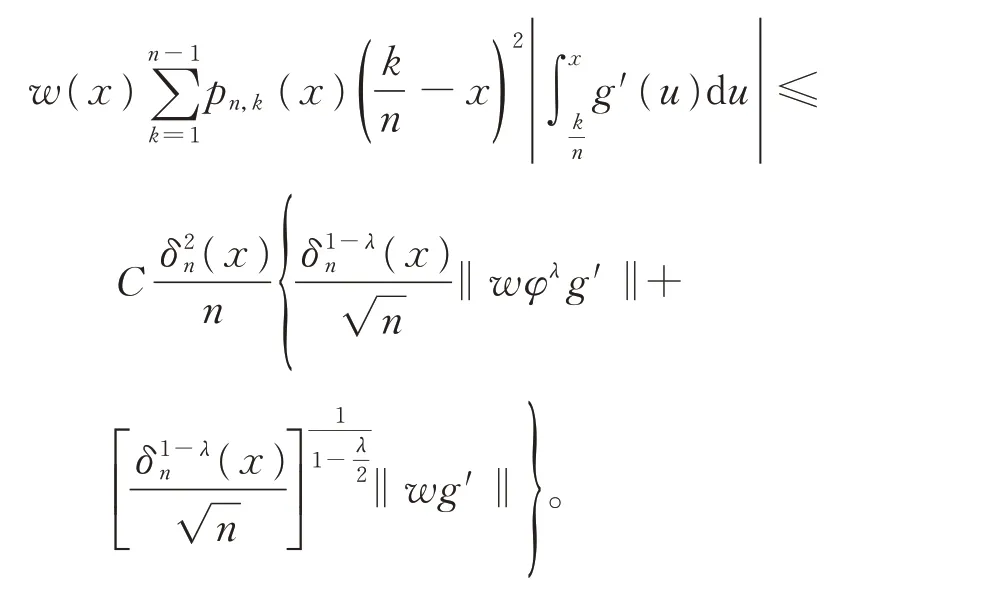
证 明（ⅰ）当时，有

1，因此

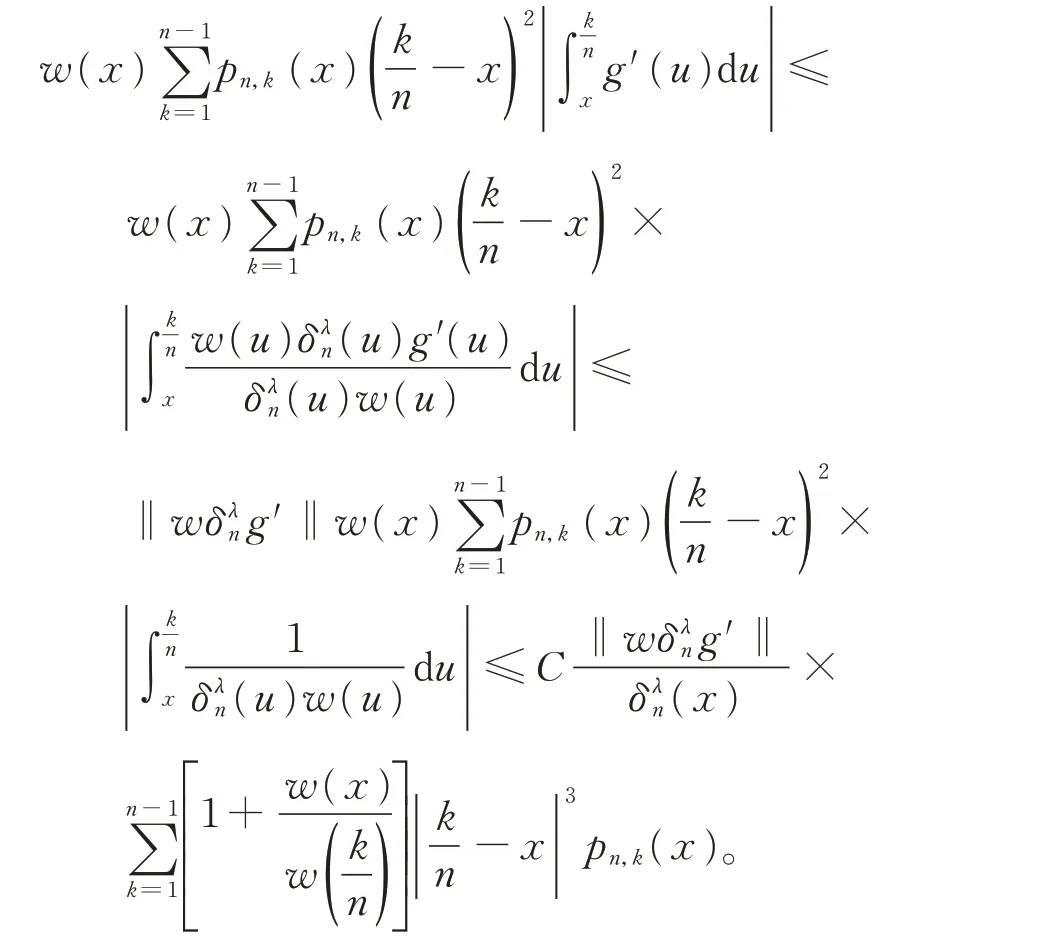
对任意的γ≥0，有［2］

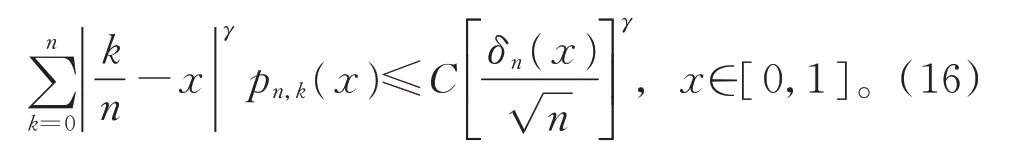
因此，

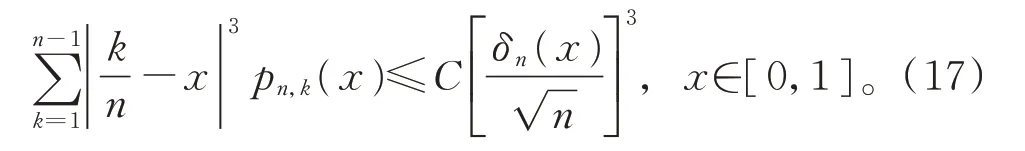
对任意的c，d＞0，有［3］

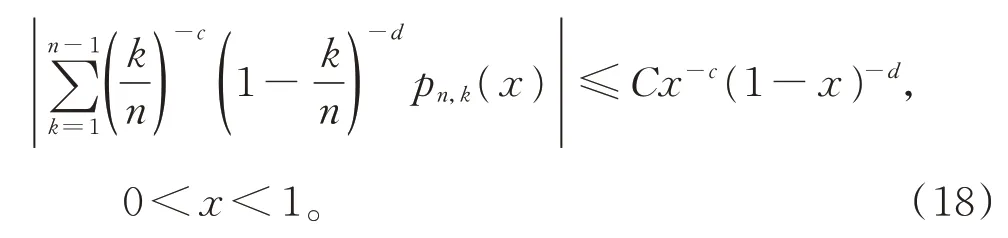
因此，

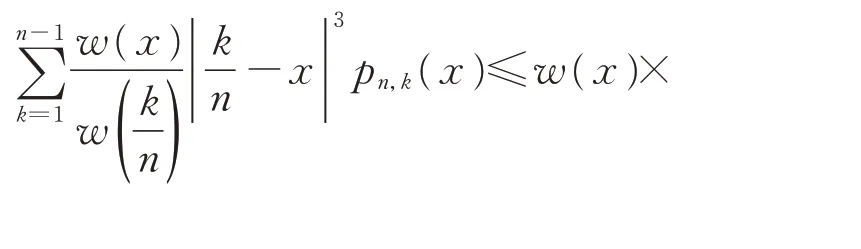
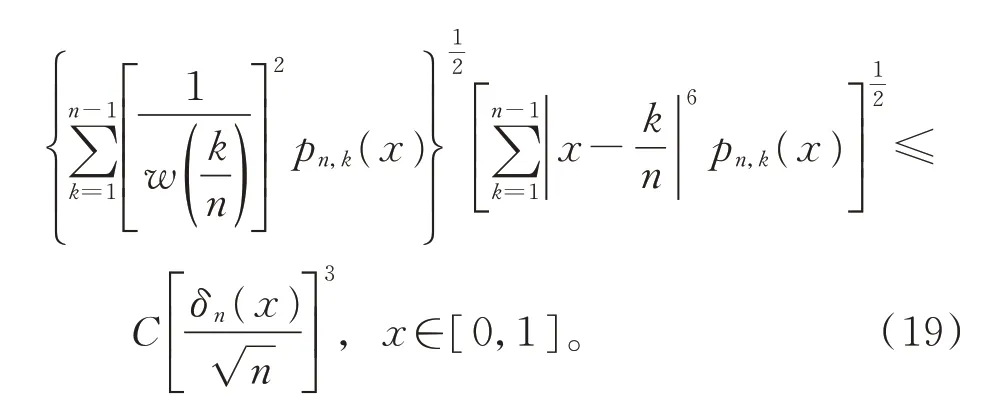
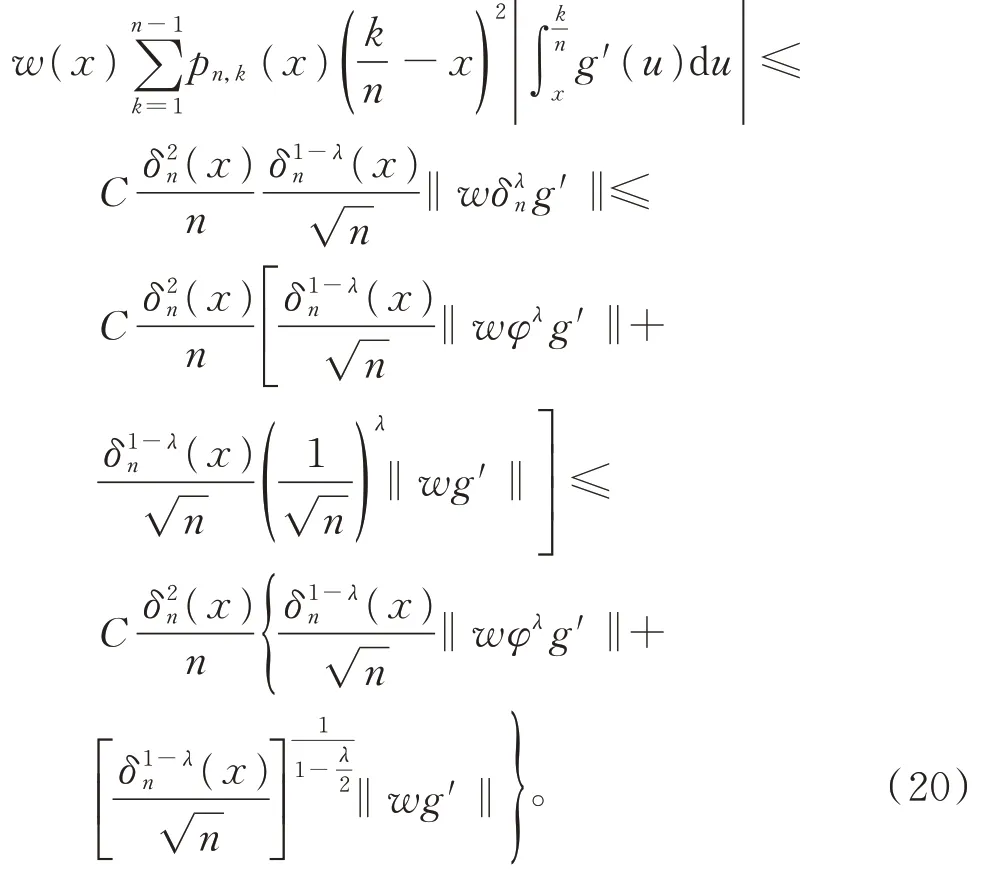
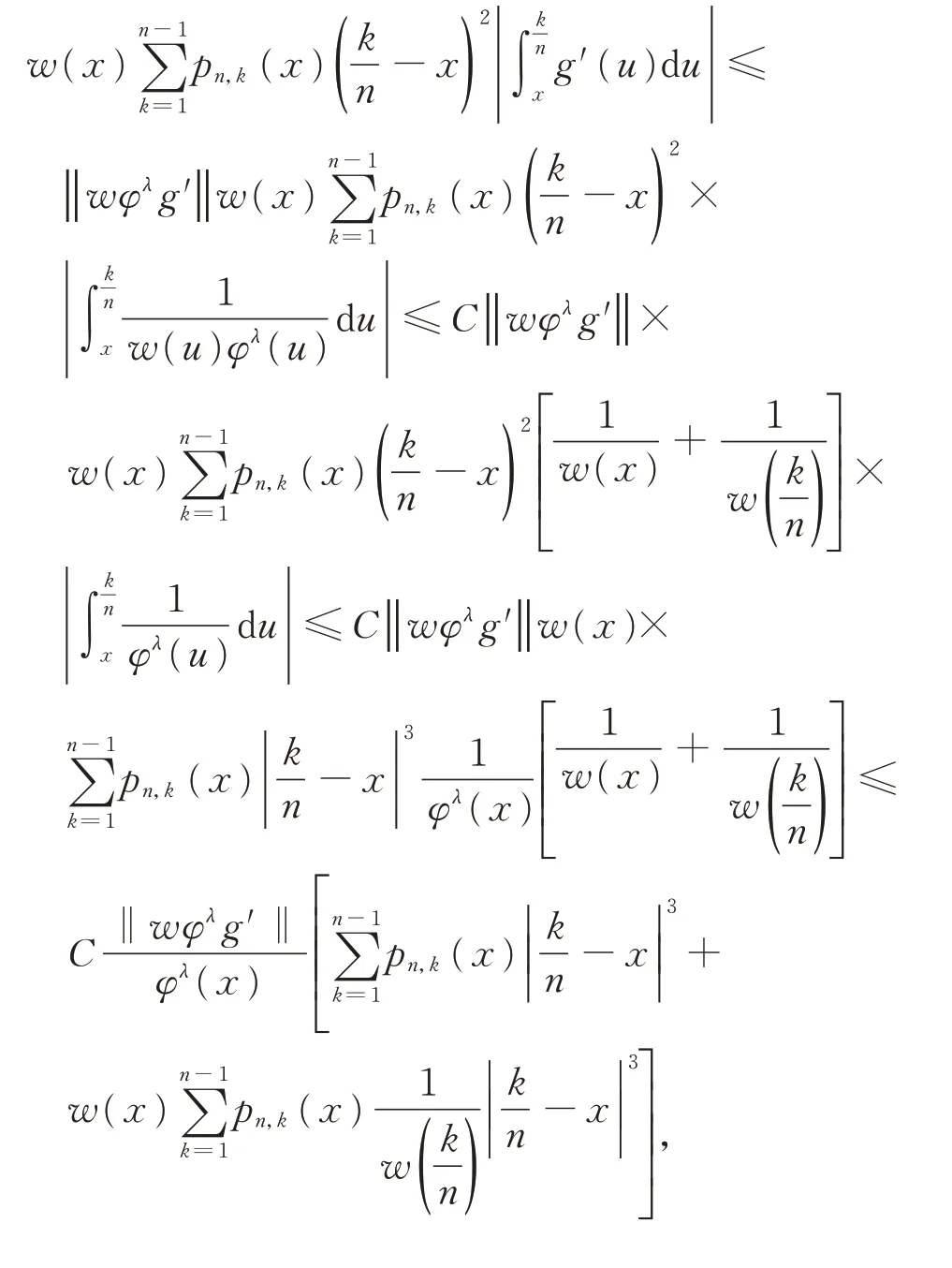
由式（16）和式（19），有

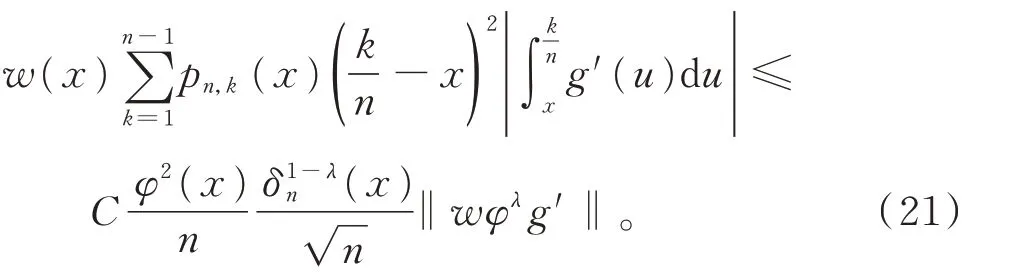
结合式（20）和式（21），引理3 得证。

2 定理3 的证明

由Taylor 展式，得

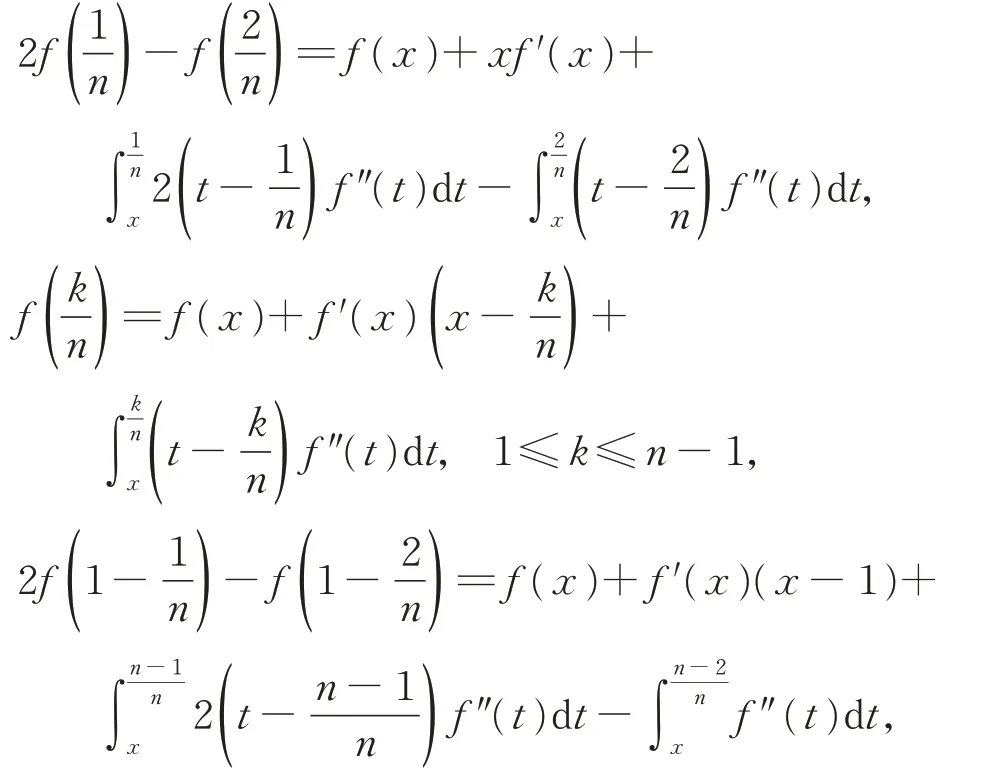
因此，

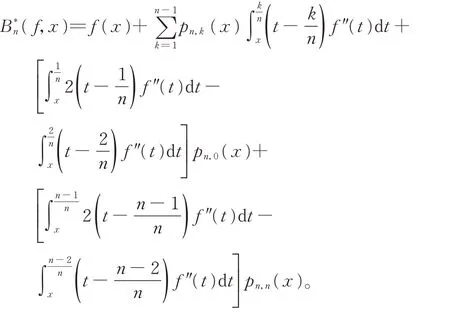
直接计算，易得，

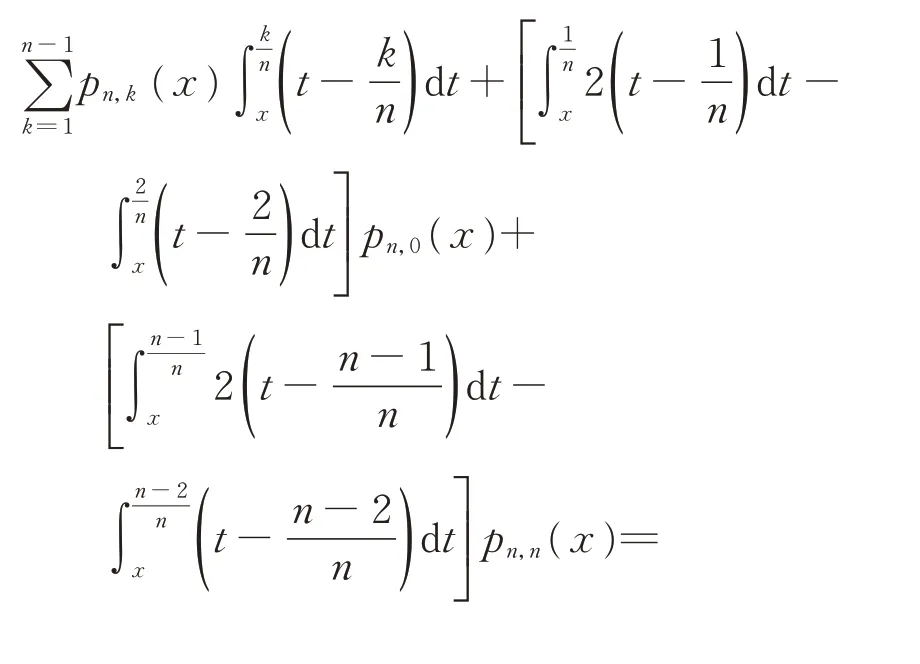
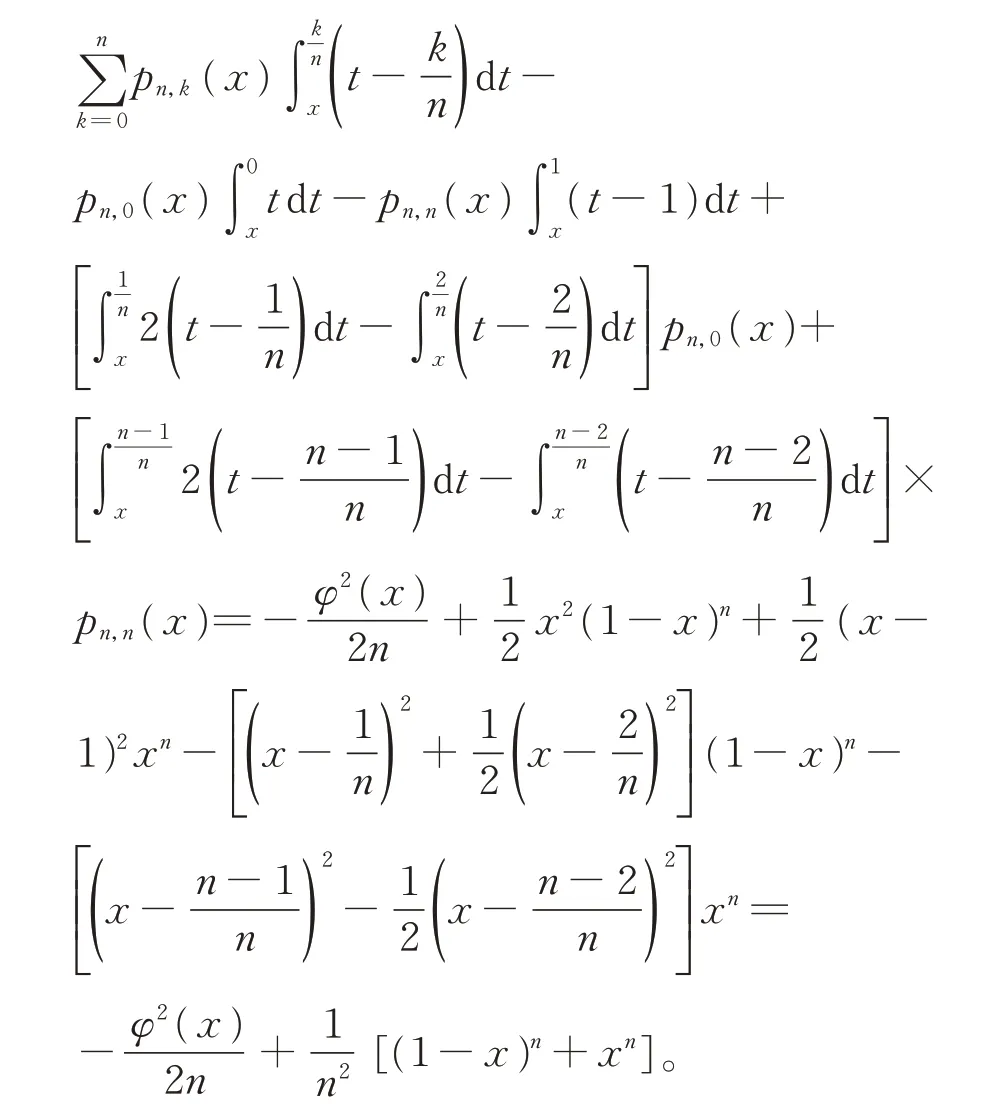
因此，有

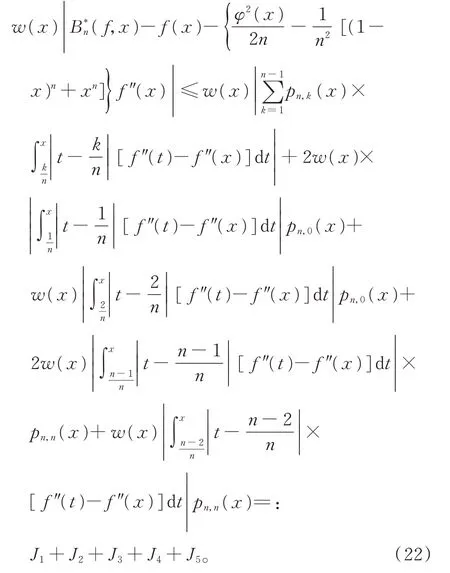
下面估计J1。取g(x)∈ACloc满足式（9）～式（11），并做以下分解：

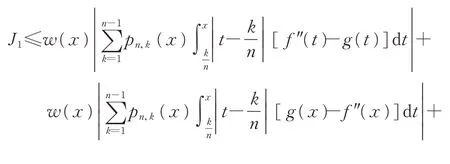
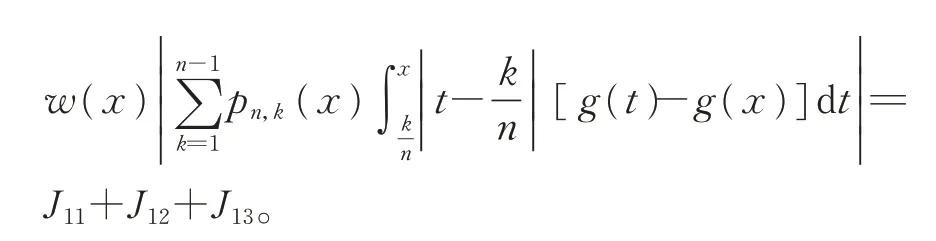
由式（16）和式（17），类似于引理3 中的推导，有

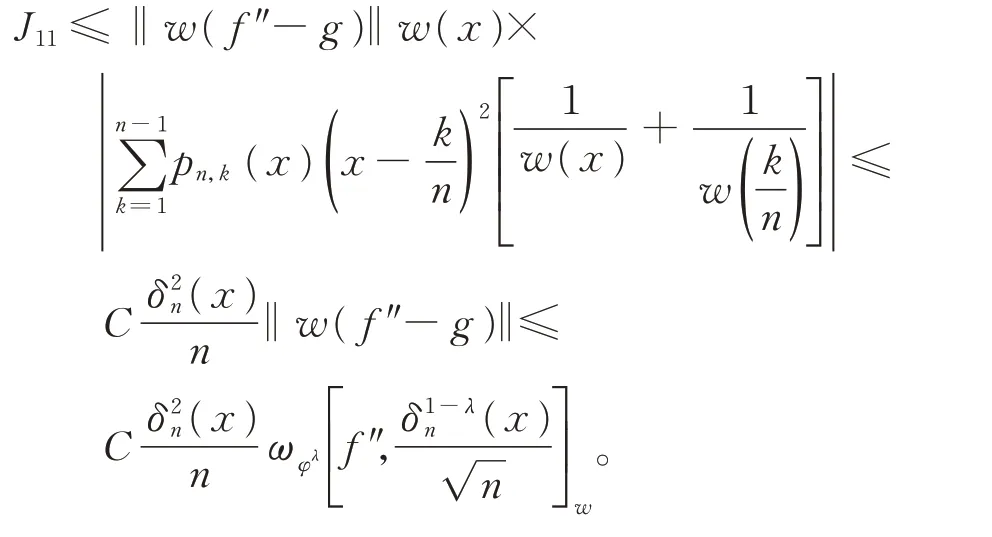
类似地，

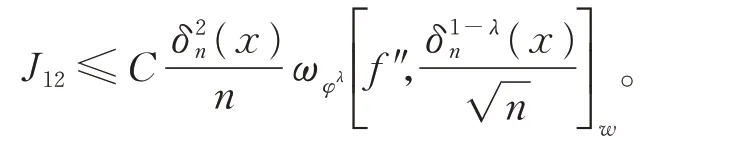
对于J13，由引理3，可得

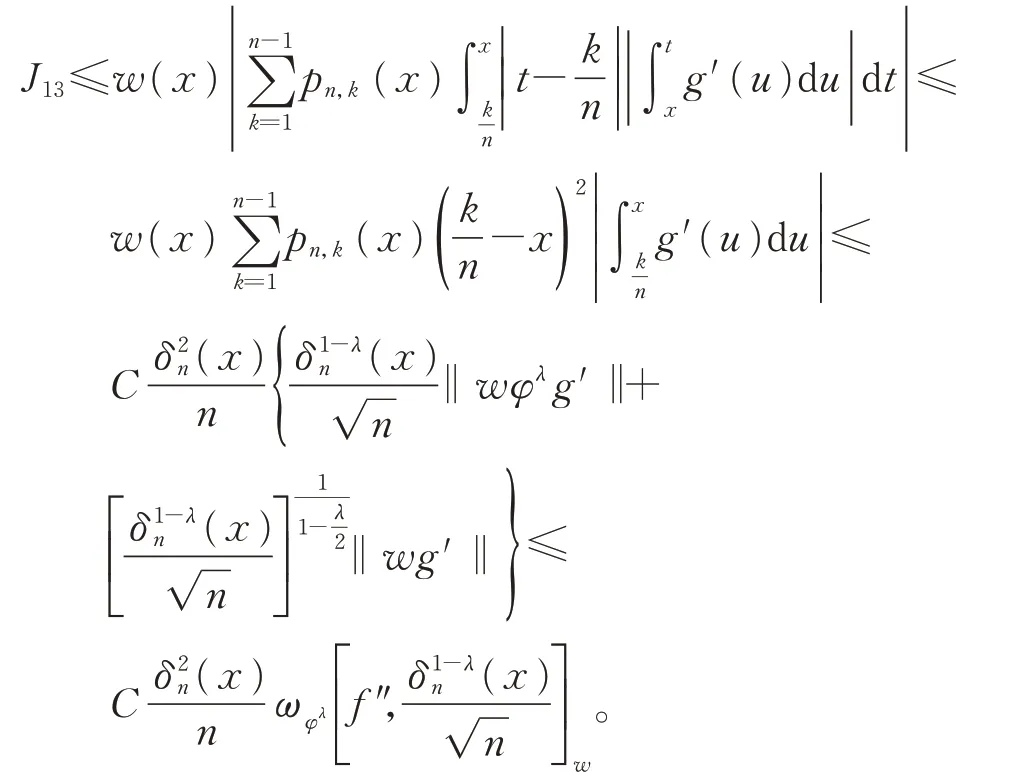
因此，

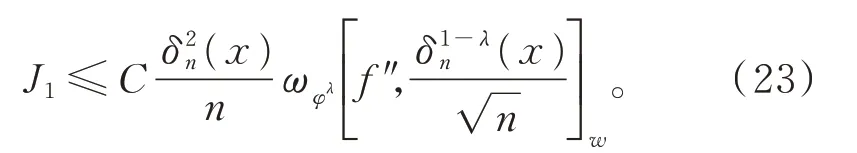
由引理2，可得

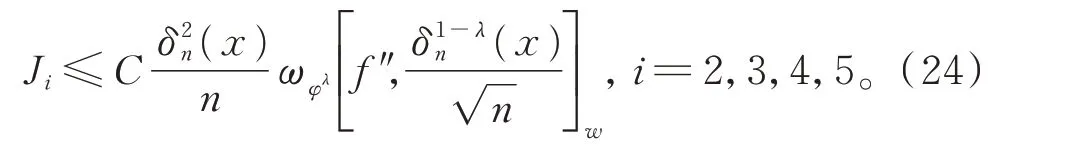
结合式（22）～式（24），定理3 得证。