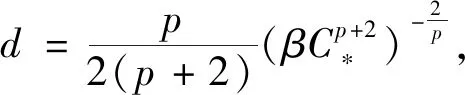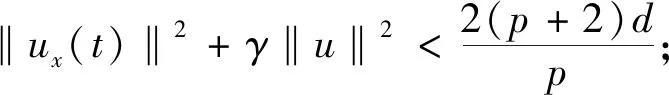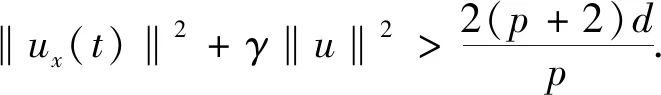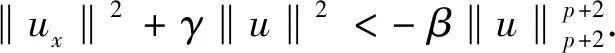一类Rosenau方程Cauchy问题整体解的存在性
王 科,华 洋
1.成都工业学院 大数据与人工智能学院,成都 611730;2.电子科技大学 数学科学学院,成都 611731
utt+uxxxxtt-γuxx+uxxxx=f(u)xx
当f(u)=β|u|pu,β≠0和初始能量E(0)>0时,利用势井方法得到了其弱解的整体存在性.
目前,在国内外有很多波浪数值模拟的理论模型,比如缓坡方程、KdV方程、Navier-Stokes方程以及Boussinesq类水波方程等.其中,荷兰数学家Korteweg和他的学生de Vries在研究浅水表面波运动时建立了KdV方程,它是能对包含弱非线性和弱色散效果的非线性系统很好逼近的模型,并在理论上证实了孤立子波的存在性.KdV方程描述了与孤立子波的产生有关的一维非简谐晶格的振动问题.近年来,人们对于KdV方程的初值问题做了大量工作,由于此方程是在假设弱非调和的条件下建立起来的模型,坡度和高振幅波的性态不能由KdV方程准确预知.在对紧离散系统的研究中,KdV方程不能描绘波与波、波与墙的相互作用关系,为了弥补KdV方程的不足,文献[1-2]提出了Rosenau方程来处理紧离散动力系统.它的两个经典方程为:
ut+uxxxxt-ux+uux=f(u)x
(1)
和
utt-γuxx+α1uxxxx+α2uxxxxtt=f(u)xx
(2)
文献[3-8]给出了这两个方程解存在性和唯一性的大量结果.文献[9]在有移动边界的区域里得到了方程(1)解的存在性.
本文将考虑方程(2)Cauchy问题解的存在性.不失一般性,在方程(2)中,假设α1=α2=1,也即我们将研究如下Rosenau方程的Cauchy问题
utt+uxxxxtt-γuxx+uxxxx=f(u)xx
(3)
u(x,0)=φ(x),ut(x,0)=ψ(x)
(4)
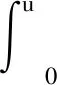
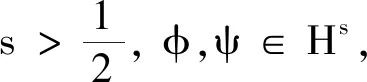
则T0=∞.
引理2[10]假设引理1的条件成立,T0>0是问题(3)-(4)解的最大存在时间,则对于所有的0 (5) 我们引入如下能量函数 (6) 和函数 (7) (8) 证由d的定义,我们得到u∈N,这里N={u∈H1{0}|I(u)=0},即I(u)=0,所以 再由(8)式得到 (9) 另一方面,由(6),(7),(8)式和I(u)=0,有 (10) 即 当f(u)=-β|u|pu时,作者建立稳定集和不稳定集,在初始能量E(0) utt-uxxtt+uxxxxtt=-αuxxxx+uxx+f(u)xx (11) 用同样的方法得到了方程(11)解的整体存在性和爆破.但是这些文献都是在低初始能量E(0) 本文分别用Lp和Hs来表示空间Lp(R)和Sobolev空间Hs(R),其范数分别为 ‖u‖p=‖u‖Lp(R)‖u‖=‖u‖L2(R)‖u‖Hs=‖u‖Hs(R) 其中 再定义一个空间 其范数为 通过(7)式,我们定义与文献[10]中不同的稳定集 K1={u∈H1|I(u)>0}∪{0} (12) 不稳定集 K2={u∈H1|I(u)<0} (13) 和势井深度 对于满足u∈C1((0,T),H1),ut∈C((0,T),H)的解u(x,t),为了在任意正能量时得到解的整体存在性,我们定义一个新的函数空间 下面证明本文中新定义的稳定集和不稳定集是不变集. 引理4(不变集) 假设f(u)=β|u|pu,β≠0,φ∈H1,ψ∈H,u(x,t)∈C1([0,T0);H1)是问题(3)-(4)的唯一解,这里T0是解的最大存在时间.如果E(0) 证因为1)和2)的证明是类似的,所以我们只需证明2).假设u(t)是问题(3)-(4)满足E(0) d≤J(u(t*))≤E(u(t*))=E(0) (14) 则由引理 3和(14)式,可得 所以 其实对于1),由I(t)和E(t)的定义有 如果I(u(t))>0,则 所以, 得证. 利用本文新定义的不变集和文献[10]中的方法也能得到文献[10]中同样的结果,这里不再赘述. 本文的主要结果如下: 定理1假设2≤s≤p+1,φ∈H1,ψ∈H,如果 E(0)>0 (15) (16) (17) 则问题(3)-(4)的解整体存在. 引理5假设u(x,t)是问题(3)-(4)带初值条件(φ,ψ)(φ∈H1,ψ∈H)的解,如果初值条件满足(15)和(17),则当u(x,t)∈WT时,映射 是严格递减的. 证我们定义 (18) 两边对t求导得到 (19) 由(3)式得到 其中X={u∈C1((0,T),H1)∩C((0,T),H)|u(x,0)=φ,ut(x,0)=ψ}. 因为u(t)∈WT,所以当t∈[0,T)时, F″(t)<0 再由(17)式得到 所以F′(0)<0.又因为F′(t) 是严格递减的. 引理6假设2≤s≤p+1,φ∈H1,ψ∈H,u(x,t)是问题(3)-(4)在最大存在区间[0,T)满足u∈C1((0,T),H1),ut∈C((0,T),H)的弱解.如果初始值满足(15)-(17)式,则u∈WT. 证我们将证明对任意的t∈[0,T),u(t)∈WT. 反证法:假设存在第一个t*∈(0,T)满足 (20) 和对任意的t∈[0,t*), (21) 由(18),(19)式和引理5可知F(t)和F′(t)在区间(0,t*)上都是严格递减的.由(17)可得对所有的t∈(0,t*), (22) 另一方面,由(5)-(7)式和引理2,可得 由(5)式有 由下面的等式 ‖utx(t*)‖2=‖utx(t*)+ux(t*)‖2-‖ux(t*)‖2-2(ux(t*),utx(t*)) 和引理5可得 (25) 所以 (26) 显而易见,(18)和(21)式矛盾.引理得证. 定理1的证明由引理 1,可知问题在最大存在区间[0,T)上有唯一的局部解.假设u(x,t)是问题满足u∈C1((0,T),H1),ut∈C((0,T),H)和(15)-(17)式的弱解.由引理6可得,u(x,t)∈WT,即当t∈[0,T)时, (27) 因而,由引理2,(5),(7)和(25)式,可得 由此可得u(x,t)和ut(x,t)分别在空间C1((0,T),H1)和空间C((0,T),H)中是有界的.所以由引理 1 可知T=∞,即问题的解整体存在.