Resistivity minimum emerges in Anderson impurity model modified with Sachdev–Ye–Kitaev interaction*

Lan Zhang(张欄), Yin Zhong(钟寅),†, and Hong-Gang Luo(罗洪刚),2,‡

1School of Physical Science and Technology&Key Laboratory for Magnetism and Magnetic Materials of the Ministry of Education,Lanzhou University,Lanzhou 730000,China

2Beijing Computational Science Research Center,Beijing 100084,China

Keywords: Anderson model,Sachdev–Ye–Kitaev interaction,non-Fermi liquid

1. Introduction

The Anderson model is at the heart position to understand Kondo physics and heavy fermion compounds.[1–7]As the first microscopic model for magnetic moments formation in metals,it implies that local moments form once the Coulomb interaction between d-electrons becomes large.[8]A low-energy effective Hamiltonian of the Anderson model is the Kondo model, which is derived from the Anderson model via the Schrieffer–Wolff transformation,[9]and it demonstrates that resistivity ultimately rises as temperature is lowered. This leads to the conduction electron’s resistivity emerges minimum versus temperature,which is one of the characteristics of the Kondo effect.[10]Correspondingly,there presents a sharppeak of the impurity electron’s spectral function at the Fermi surface, i.e., a Kondo resonance, when the Kondo screening appears to quench the local moments.[6]The evolution from localized magnetic moment state to the non-magnetic state,i.e., from Landau Fermi liquid to the localized Landau Fermi liquid,is a crossover among some rare-earth alloy and actinide compounds.[5,6]

The Landau Fermi liquid theory has been the workhorse of the physics of interacting electrons for over 60 years.[11]However, some heavy-fermion quantum critical compounds such as CeCu6−xAux, YbRh2Si2and β-YbAlB4display the non-Fermi liquid(NFL)behavior in which the transport properties and specific heat capacity cannot be derived from the Fermi liquid(FL)theory.[12–14]This attracts much attention to the NFL behavior, and many theories have been proposed to interpret this phenomenon.[15–21]The lack of controlled theoretical techniques hinders the understanding of the strong electron correlation in the NFL;nevertheless,the invention of the Sachdev–Ye–Kitaev (SYK) model provides a chance to understand the correlation physics in related systems accurately since its solvable nature.[22–25]

The SYK model is a quantum many-body model with random all-to-all interactions for fermions, which was studied in the 1990s and later as models for novel NFL or spinglass states.[26–32]It provides a solvable example in zero dimension and has been extended to higher dimensions.[33–39]In recent years, many exotic physical phenomena have been found in SYK models, e.g., supersymmetry,[40]quantum chaos,[34,41–43]many-body localization,[44,45]strongly correlated metal,[46,47]and quantum phase transition.[24,25,48–51]

In a recent work[52]with an aim to provide a solvable model for a heavy-fermion system,the standard periodic Anderson model was modified with the SYK random interaction.This modified model was found to have a low temperature FL, and more interestingly, an NFL solution at elevated temperature and the rising of resistivity at high temperature can be attributed to the single SYK quantum impurity.[52]In the present paper, we consider the distinction between the impurity and the lattice models and study the SYK quantum impurity problem, modeled by the Anderson model with SYK random interaction. We call it Sachdev–Ye–Kitaev Anderson model(SYKAM).Importantly,SYKAM provides an interesting and counterintuitive example where resistivity minimum exists in the absence of Kondo resonance. In a conventional picture, the resistivity minimum is due to the formation of Kondo resonance.

Fig.1. Schematic phase diagram of the SYKAM. Our system has an FL behavior at T T⋆,while it is FG at T ≫T⋆.

Under the large-N limit, the qualitative analysis of the conduction electron resistivity ρcelucidates that the SYKAM behaves as an FL when temperature T T⋆, where T⋆is a scaling temperature.The quantitative calculation gives a phase diagram as shown in Fig.1,where ρcexists a minimum at temperature T⋆,demonstrating SYKAM behaves as an FL when T T⋆,and at high temperature T ≫T⋆,a free Fermi gas(FG)forms in SYKAM.It is emphasized that the NFL does not display in the standard Anderson model.From impurity electron’s entropy Sdand specific heat capacity Cv, a crossover, not a phase transition, exists between FL and the NFL. This is confirmed by a renormalization group(RG) analysis, whose flow equation is similar to the Kondo problem.[1–5]

What is the relation between the standard Anderson and the SYK model? Compared with the standard Anderson model, the SYK random interaction does not provide localized interaction to the onsite different impurity spin states,leading to no local moment forming in our model. The hybridization between conduction and impurity electrons contributes to extending the localized impurity electron’s density of state(DOS)to the Lorentz-like lineshape,and the impurity electron has the scattering with conduction electron sea, but its DOS shows that there is no sharp-peak at the Fermi surface like the Kondo resonance.[5,6,53,54]The resistivity minimum emerges in our model when the system behaves as an NFL rather than FL, while the system is localized FL when it presents the resistivity minimum in the standard Anderson model. Compared with the SYK model, our model includes the hybridization between the conduction electrons and the impurity electron. Such hybridization has an effect on the transport property;the resistivity is a constant line when V =0 and has the resistivity minimum when hybridization is available,which the random interaction SYK system does not have.Both the SYK model,the standard Anderson model,and our model have similar thermodynamic properties (the entropy and the specific heat capacity). Our model and the standard Anderson model have the resistivity minimum, but the resistivity minimum emerges in our model approaching the non-Fermi liquid regime. Since the resistivity minimum and the Kondo resonance are two characteristics of the Kondo effect, in which the conduction electron screens the impurity electron’s local moments.[5,6,53,54]The Kondo resonance is the most important feature to detect Kondo screening,and the resistivity minimum may be not enough to interpret the Kondo effect.

The paper is organized as follows. In Section 2,we introduce SYKAM and derive self-energy and the impurity electron Green’s function. In Section 3,we present the conduction electron resistivity ρc. In Section 4, we compute thermodynamical behaviors of our model, i.e., impurity electron’s entropy Sdand its specific heat capacity Cv. In Section 5, we apply RG theory to analyze the above results. Finally, Section 6 is devoted to a brief conclusion and perspective.

2. Model and method

The Hamiltonian of SYKAM can be written as

Fig.2. (a) Schematic crystal lattice of SYKAM, where the red dots are the conduction electrons,and the black dots are the impurity electron pseudospin states. (b)The SYK random interaction Uijml between different impurity electron pseudospin states 1,2,...,16,...,N.

To solve the mentioned model Eq. (1), we consider the large-N limit as done in the SYK model,which means that the number of the component of pseudospin j=1,2,...,N is artificially enlarged to infinity. As a result,the partition function of our system can be approximated by its saddle point value(see the appendix). Equivalently,the large-N limit means that after the disorder average over Uijkl,the self-energy of impurity electron Σ(iωn)is dominated by the watermelon diagram as shown in Fig.3,

Therefore,via the Dyson equation,the resulting Green’s function for the impurity electron reads

where ωn=(2n+1)πT denotes the fermionic Matsubara frequency with n=0,±1,±2,...,±∞.

Fig.3. The leading impurity electron self-energy Feynman diagrams for SYKAM under the large-N limit. (a) is the bare interaction vertex before average over random interaction Uijml. (b) illustrates the selfenergy after average.

For conduction electron, its Green’s function Gc(k,iωn)is derived from the equation of motion[5]and reads

Consequently,Gd(iωn)and Gc(k,iωn)can be found by solving Eqs.(2)–(4)self-consistently.

When D ≫|ωn|,we get

According to the Feynman diagrams, we can get the impurity electron self-energy

Therefore, we can obtain Gd(iωn) and Gc(k,iωn) by solving Eqs.(4),(6),and(7)self-consistently. Before presenting the numerical results, one can inspect two limiting cases(weak and strong coupling)and extract useful analytic formulas.

2.1. Weak coupling limit

In the weak coupling limit, the self-energy correction Σ(iωn) is assumed to be small compared with the free part iωn−Ed+i∆in Gd(iωn). At zero temperature, one can use non-interacting impurity electron Green’s function

and we use the analytic continuation iωn→ω+iδ to get the zero temperature impurity electron self-energy

which indicates a local FL behavior.[56]Via the Kramers–Kronig relation,its real part is ReΣ(ω)∝ω.[6]

We conclude that the system behaves like a local FL in the weak coupling limit, which is similar to the ground state of the standard Anderson impurity model.[5]

2.2. Strong coupling limit

In the strong coupling limit, the self-energy correction Σ(iωn) seems to be large. If Σ(iωn)≫∆, one can approximate impurity electron Green’s function as

which is identical to the cases in the SYK models. Thus,analytic continuation,the self-energy is found to be

the quasiparticle weight is defined as

which corresponds to the NFL behavior.[38]

Therefore, at strong coupling, the self-energy should be approximated a mixture of FL and SYK form as

where ΣFL(ω)has an FL-like form.

Combining the results from weak and strong coupling analysis, one finds that our system is always an (local) FL at low-temperature or low energy below a characteristic energy scale E*. When elevating temperature or jumping into high energy regime above E*, the NFL behavior is driven by the SYK interaction.

3. Transport properties

Before performing calculations of transport quantities,we inspect the behavior of the single-particle Green’s functions.

and here we set Boltzmann’s constant kB=1,we have

At|ω|≫E⋆,the impurity electron Green’s function is dominated by the self-energy term and has an NFL feature. When|ω|≪E⋆,it shows FL-like behavior,the detailed formulas of Green’s function of the impurity electron and the conduction electron are given in the appendix.

Since the static resistivity is inversely proportional to the static limit of optical conductivity, we can compute the latter quantitatively via the Kubo formula[6]

and

denotes the current–current response function. Here, the xcomponent of current operator ˆJxis given by[57]

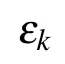
where the spectral function of conduction electrons is given in the appendix.

Thus,the resistivity is constant at zero temperature.

It means that our system behaves as FL at low temperature and has the NFL behavior at high temperature.

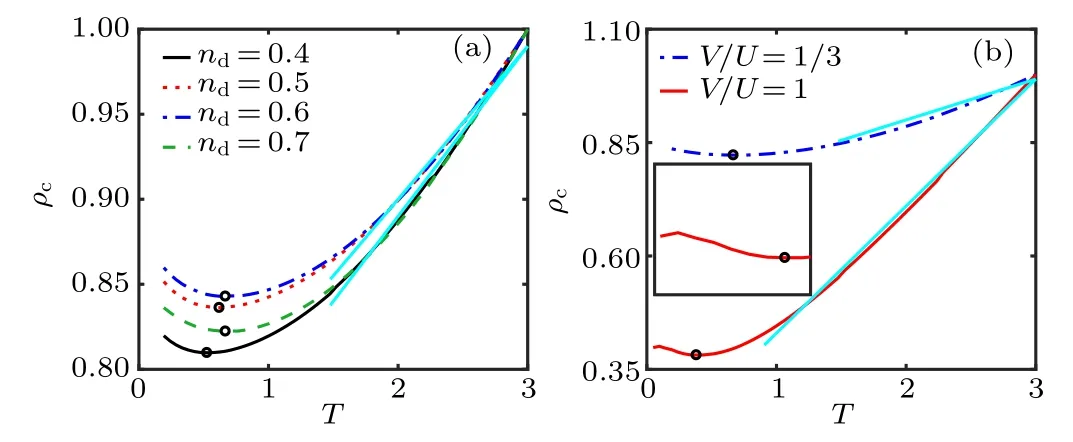
Fig.4. The conduction electron resistivity ρc as a function of temperature T.For the different impurity electron concentrations nd as shown in(a),the black dots are T⋆=0.5246,0.6198,0.6674,0.6674 for nd=0.4,0.5,0.6,0.7,and the parameters are V =1,U=3,D=12,Ed=−U/2.In (b), ρc versus V/U at nd =0.7, the blue dashed line is the same as nd=0.7 in(a),and the red solid line is V/U =1/3 with T⋆=0.3818,the inset shows the low temperature case of ρc, where parameters are V =1,U =1,D=4,Ed =−U/2. The cyan lines are the basic linear fitting,which shows that ρc(T)∝T at T >T⋆.

Due to the impurity,electron occupation ndis

where Ad(ω)is the spectral function of the impurity electron,f(x)=1/[e(x−µ)/T+1]is the Fermi–Dirac distribution function,µ is the system’s chemical potential for both conduction and the impurity electrons. Because the system has just one impurity electron with N pseudospins, we take the chemical potential asµcin our work. When we fixed the impurity electron occupation nd, Ad(ω) and f(ω) change versus temperature T,and the conduction electron spectral function Ac(k,ω)also change according to Eq. (A4). From Eq. (16), we plot the conduction electron resistivity ρcversus T at the impurity electron occupation nd=0.4,0.5,0.6,0.7,as shown in Fig.4.For the case of the fixed conduction electron occupation, the detailed discussion is given in the appendix.

In Fig.4, the conduction electron resistivity ρchas a minimum at T⋆, which is similar to the Kondo effect.[5,6,60]When temperature T >T⋆,the line of nd=0.4 coincides with nd=0.7, which is similar to nd=0.5 and nd=0.6. At low temperature T T⋆, where the system behaves as the NFL.In Fig.4(b),it demonstrates that the line of V/U =1/3 with D=12 has a higher T⋆than V/U =1 with D=4, where the wide bandwidth 2D and the large random interaction U also induces a high T⋆, which coincides with Eq. (12). The red solid line of Fig.4(b) has the constant resistivity at low temperature as shown in the inset, which also demonstrates that our system has FL behavior at T T⋆because of linear resistivity,when T ≫T⋆the system has the FG behavior as shown in Fig.1.

We also have shown the conduction electron resistivity ρcversus temperature T for Ed=0,U/2 at different impurity concentrations nd=0.4,0.5,0.6,0.7 in Fig.5.Compared with Fig.4,both resistivity lines have the minimum and the larger Edinduces the smaller T⋆. It demonstrates that SYKAM is not symmetric around nd=0.5. Our model is different from the single-impurity Anderson model; the symmetric Anderson model Ed=−U/2 has the particle-hole symmetry around nd=0.5.[5]However,our model has the four-body SYK random all-to-all interaction, in contrast to the onsite two-body Coulomb interaction, which is not satisfied with the particlehole symmetry except for the case Uijml=0.

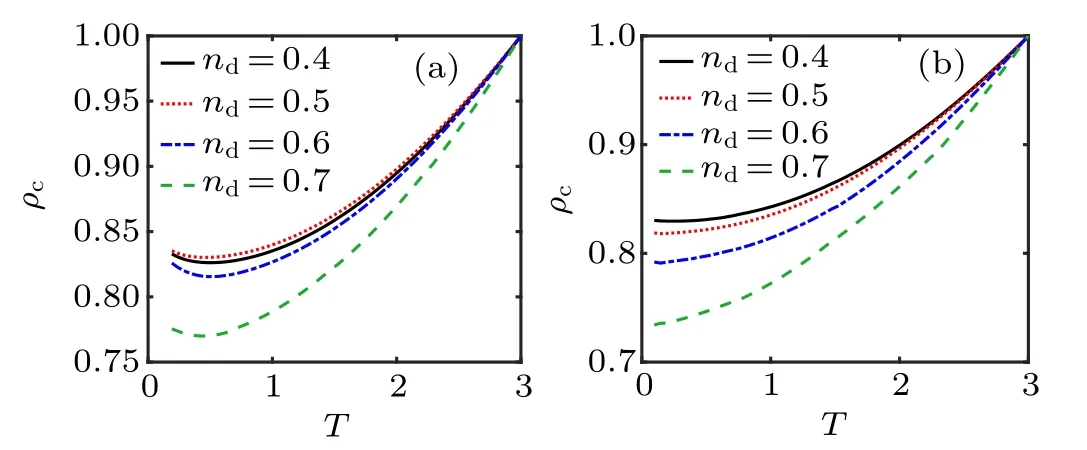
Fig.5. The conduction electron resistivity ρc as a function of temperature T for the different impurity electron concentrations nd =0.4, 0.5,0.6, 0.7, respectively. (a) is the case Ed =0. (b) is the case Ed =1.5.The parameters are V =1,U =3,D=12.

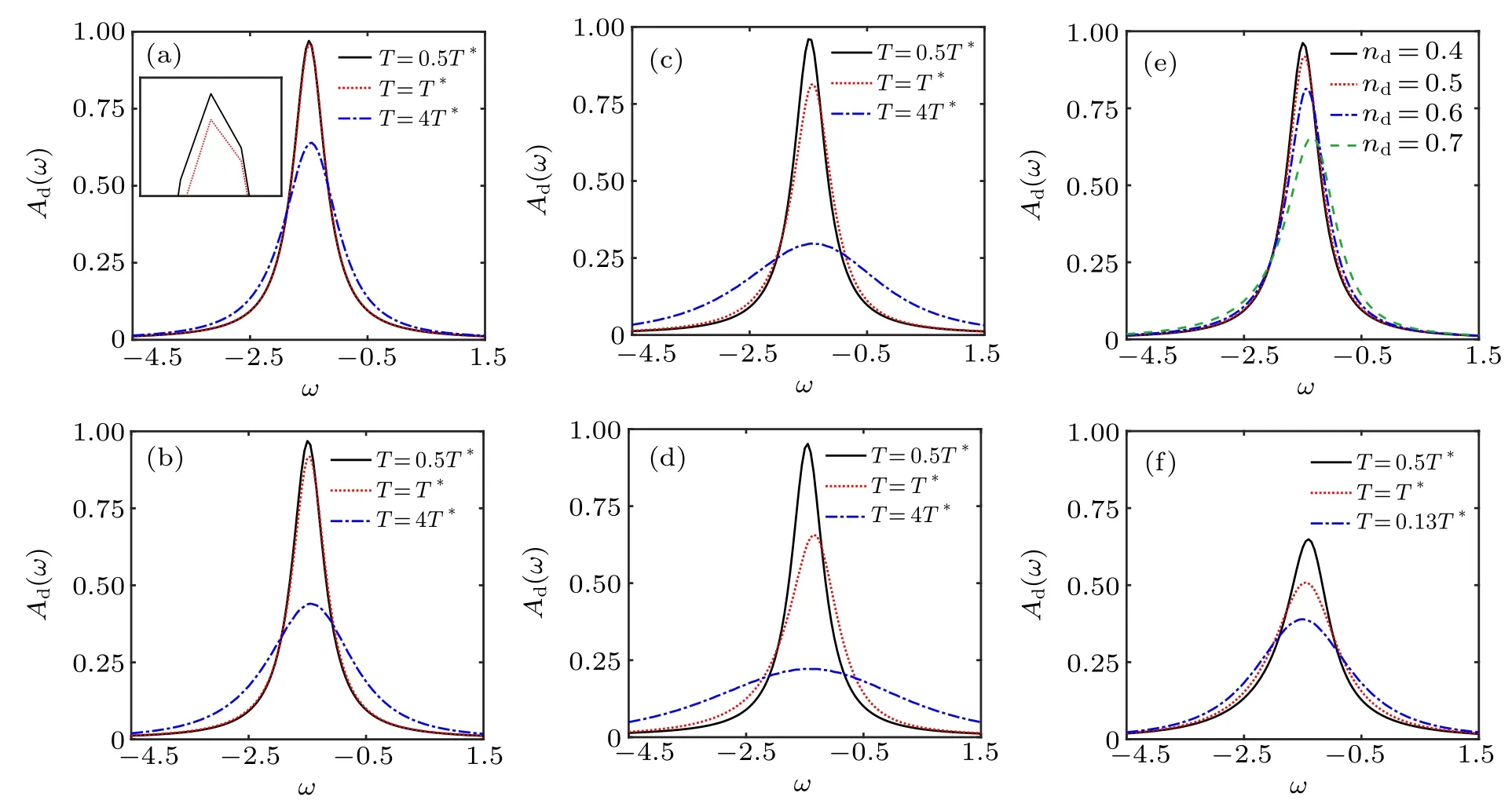
Fig.6. The impurity electron DOS Ad(ω)as a function of the frequency ω. (a)–(d)are for different temperature T with the limited impurity electron concentrations nd =0.4,0.5,0.6,0.7; the inset of(a)shows that two lines are not merged together. (e)describes Ad(ω)versus nd at T⋆=0.5246,0.6198,0.6674,0.6674,respectively. The parameters of(a)–(e)are V =1,U=3,D=12,Ed=−U/2. In(f),all lines are plotted with V =1,U =1,D=4,Ed=−U/2 at nd=0.7,and T⋆=0.3818,where the black solid line is the DOS of FL at the constant resistivity.

Since the resistivity has the similarity as the Kondo effect,we also compute the DOS of the impurity electron

which is shown in Fig.6. At the fixed impurity electron concentrations,peaks of the impurity electron DOS decrease versus temperature, and lines of Ad(ω)become broad, as shown in Figs.6(a)–6(d). The black solid lines of Figs.6(a)–6(d)and 6(f)are the case that the system behaves as FL,the red dotted lines of Figs.6(a)–6(d)and 6(f)are the case of T =T⋆,while blue dashed lines of Figs.6(a)–6(d)and 6(f)are the case that the system behaves as the NFL.When T =T⋆,peaks of Ad(ω)decrease versus nd, as shown in Fig.6(e). In Fig.6(f), both lines are similar to Figs. 6(a)–6(d), but Ad(ω) has a smaller peak than Fig.6(d)at T⋆on account of the smaller conduction electron bandwidth.

Compared with the SYK model, our model has the hybridization between the conduction electrons and the impurity electron, while the standard SYK model does not have the hybridization, but the Lorentz lineshape of the impurity electron DOS is similar to the SYK model. Compared with the single-impurity Anderson model, our model has the random four-body SYK interaction between different pseudospin states of the impurity electron not the onsite Coulomb interaction between different impurity spins(spin up and spin down),which does not induce the sharp-peak like the Kondo resonance around the Fermi surface, while the single-impurity Anderson model has the Kondo resonance around the Fermi surface.[5,6,53,54]

4. Thermodynamics

The impurity electron contributes a free-energy as

According to Eq.(18),the system behaves as an FL at low temperature, while at high temperature it is an NFL. Due to Refs.[24]and[48],there may exist a quantum phase transition in our model. We have got its entropy Sdand specific heat capacity Cvversus temperature T by Eq.(22),which is shown in Fig.7. For intermediate-T,Sdincreases with nd. All Sdgradually approach saturation at high-T limit with limT→∞Sd=ln2,as shown in Fig.7(a).[39,61]Cvhas a maximum at intermediate-T,which is similar to the SYK model.[39,62]Cvincreases with ndat low temperature,while it decreases for high temperature.

Since entropy and specific heat capacity are continuous and smooth,we expect a crossover,instead of phase transition,between FL and the NFL.Interestingly,similar transport properties also display in Kondo physics,and dilute magnetic alloy systems undergo a crossover from free local moment state to the non-magnetic FL state.[5,6]

Fig.7. The thermodynamics of our model as a function of temperature T, for different impurity electron concentrations nd. (a) The entropy Sd and (b) the specific heat capacity Cv of the impurity electron. The parameters are V =1,U =3,D=12,Ed=−U/2.

The two systems have similar transport and thermodynamics, and they undergo a crossover rather than phase transition.[5]Although both systems have the scattering between conduction electrons and the impurity electron, the DOS of the impurity electron is significantly different. Moreover,SYKAM has an NFL behavior ρc(T)∝T at temperature T >T⋆,while the Kondo screening is the localized FL below Kondo temperature and the NFL behavior does not appear in the standard Anderson model. Since no symmetry-breaking is involved,a crossover is expected between the FL and the NFL,and thermodynamics can not be used to detect crossover due to the lack of singularity.

5. Renormalization group analysis

In order to renormalize our model, we have a parameter λ(λ >1)to cut off the fermionic Matsubara frequency ωnand divide our model into the low energy part and the high energy part as follows:

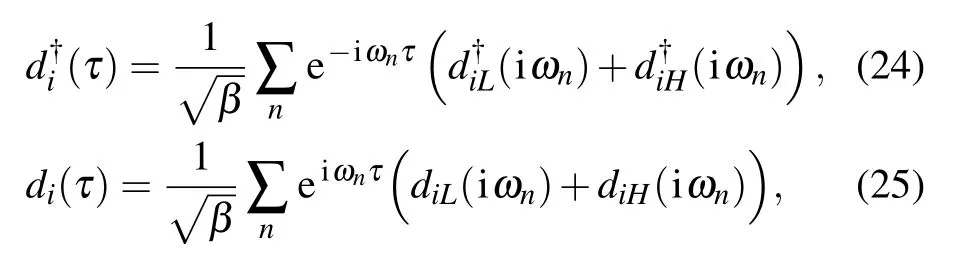
The effective action is given by

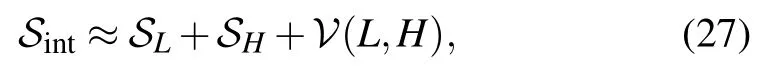
In the light of the first-order and second-order correction,the detailed calculations are shown in the appendix, and the RG transformation relation can be written as

We set λ = el,and its flow equation is

In the fixed points, the scaling invariance has a consequence dU2/dl = 0; it demonstrates that SYKAM has two fixed points U2=0 and U2=∞, as shown in Fig.8. For U2=0,it scales to a weak coupling repulsive fixed point,forming FG.U2=∞is a strong coupling attractive fixed point of FL.Scaling proceeds from a repulsive fixed point via a crossover to an attractive fixed point,in which exists an NFL at finite U2.

Fig.8. Schematic illustration of RG flow in the SYKAM.For U2=0,it scales to a weak coupling fixed point, forming the FG.U2 =∞is a strong coupling fixed point of FL. Here the weak and strong coupling does not mean the weak coupling limit and the strong coupling limit in this paper. Scaling proceeds from a repulsive fixed point via a crossover to an attractive fixed point,in which exists an NFL at finite U2.

6. Summary and perspective

We have computed the transport and thermodynamics of SYKAM,which demonstrates that the NFL exists at temperature T >T⋆. The RG analysis shows a crossover between FG(U2=0)and FL(U2=∞), which presents the NFL at finite U2. The impurity electron’s entropy Sdand the specific heat capacity Cvexhibit the similarity to the SYK model and the Kondo system.[5,39,62]The resistivity of SYKAM has a minimum at temperature T⋆,similar to Kondo temperature,but the impurity electron DOS of SYKAM does not have the sharp Kondo resonance peak around the Fermi surface.[5,6]

Our model is an extension of the single-impurity Anderson model and the SYK model. Comparing with the singleimpurity Anderson model, the SYK random interaction can not provide the localized interaction to the onsite different impurity spin states,so our system does not form local moments.Compared to the SYK model, our system has the hybridization between the conduction electrons and impurity electron,which is present in the Kondo systems but does not exist in the SYK model. The resistivity minimum emerges in SYKAM when it behaves like an NFL,where the impurity electron has the SYK interaction without Coulomb interaction. Anderson model and our model both have the scattering between the conduction electrons and the impurity electron because of the hybridization, and except that the DOS of the impurity electron does not display the sharp-peak as the Kondo resonance and not have the localized magnetic moments in SYKAM.

Finally,it may be helpful to lead to a new route to realize the Kondo systems(heavy-fermion compounds,various quantum dot devices, and novel material Kondo systems) and the SYK physics. With the development of ultracold atom technique for realizing the Kondo lattice model,[63–65]our results may be protocolled in near-future experiments.

Appendix A:Transport properties

When|ω|≪E⋆,it shows FL-like behavior,Green’s function of the impurity electron and the conduction electron,i.e.,(T =0)

The spectral function of conduction electrons is

According to Eq.(16),we have presented the conduction electron resistivity ρcversus temperature T with fixed nd(tuning the chemical potential), as shown in Figs.4 and 5. However,when we fix ncby tuning the chemical potential,the conduction electron resistivity ρcis changed versus temperature T. We have plot conduction electron resistivity ρcas a function of temperature T at the conduction electron concentration nc=0.4, as shown in Fig.A1. It shows that the conduction electron resistivity ρcemerges a minimum versus temperature T when fixed the conduction electron occupation nc, which behaves like that in the Kondo effect.[5,6,60]

Fig.A1.The conduction electron resistivity ρc as a function of temperature T at the conduction electron concentration nc=0.4,the red dashed line is the impurity electron concentration nd=0.4,the parameters are V =1,U =3,D=12,Ed=−U/2.

Appendix B:Thermodynamics

Here the non-interacting action is

with imaginary time τ ∈[0,β] (β =1/T) and ckj, djare the anticommuting Grassman fields. The SYK interaction reads

After performing the standard Gaussian random average over each independent Uijmland focusing on one replica realization,[46]we obtain